苏教版高中选修3-3 3.1.2 球面的对称性
文档属性
| 名称 | 苏教版高中选修3-3 3.1.2 球面的对称性 |

|
|
| 格式 | zip | ||
| 文件大小 | 576.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 00:00:00 | ||
图片预览





文档简介
课件15张PPT。§ 3.1.2 球面的对称性 从表面上看,你可能觉得球面是一个比较简单的几何图形. 然而,事实并非如此,球面有许多独特而有趣的性质. 事实上,球面作为空间中最完美的图形之一,具有很强的对称性,所以能给我们带来强烈的视觉美感.知识回顾 我们都已经学过,画一条线段,以线段长为半径,以一端点为圆心画弧绕360o后得到圆. 同样,由圆的对称性可知圆是轴对称图形,其对称轴是任意一条通过圆心的直线.圆也是中心对称图形,其对称中心是圆心. O问题:
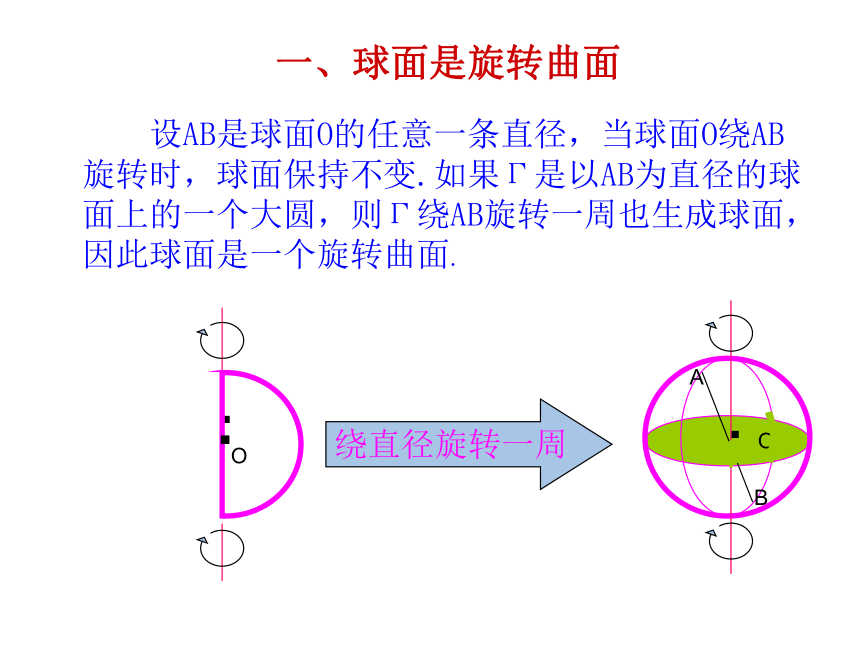
球面具有哪些对称性?探索球的对称性 通过一些计算机软件,如几何画板,我们可以进行一些有趣的试验,来进一步探索球的对称性,深化对球面性质的理解. 设AB是球面O的任意一条直径,当球面O绕AB
旋转时,球面保持不变.如果Γ是以AB为直径的球
面上的一个大圆,则Γ绕AB旋转一周也生成球面,
因此球面是一个旋转曲面.一、球面是旋转曲面绕直径旋转一周 O ...OAB 海豹将球顶在头上旋转,在此过程中,球面始终与初始球面旋转对称.二、球面关于它的任一直径对称 取定一条直径AB,对于球面上的任一点P(P不取A,B),可以找到球面上的另一点P',使线段PP'与AB垂直相交,且交点就是PP'的中点.这样的两点P,P'是球面上关于直线AB的对称点,如图,因此球面关于它的任一直径对称.OPP' 对于球面上任意一点 A,假设它关于球心的对称点为A' ,则由 A和 A'到球心的距离相等可知,点 A' 到球心的距离等于半径,即点 A' 一定在这个球面上.
球心O是对称中心,一对对径点是关于球心O的对称点.三、球面是中心对称图形中心对称图形四、球面关于过球心的平面对称 如图,过球心的平面与球面交于一个大圆,球面关于过球心的平面是对称的. 球面上关于直径的旋转,关于球心、直径、过球心的平面的对称也叫做球面上的运动.
课堂小结1.球面是旋转曲面 2.球面关于它的任一直径对称 3.球面是中心对称图形4.球面关于过球心的平面对称谢谢指导!
球面具有哪些对称性?探索球的对称性 通过一些计算机软件,如几何画板,我们可以进行一些有趣的试验,来进一步探索球的对称性,深化对球面性质的理解. 设AB是球面O的任意一条直径,当球面O绕AB
旋转时,球面保持不变.如果Γ是以AB为直径的球
面上的一个大圆,则Γ绕AB旋转一周也生成球面,
因此球面是一个旋转曲面.一、球面是旋转曲面绕直径旋转一周 O ...OAB 海豹将球顶在头上旋转,在此过程中,球面始终与初始球面旋转对称.二、球面关于它的任一直径对称 取定一条直径AB,对于球面上的任一点P(P不取A,B),可以找到球面上的另一点P',使线段PP'与AB垂直相交,且交点就是PP'的中点.这样的两点P,P'是球面上关于直线AB的对称点,如图,因此球面关于它的任一直径对称.OPP' 对于球面上任意一点 A,假设它关于球心的对称点为A' ,则由 A和 A'到球心的距离相等可知,点 A' 到球心的距离等于半径,即点 A' 一定在这个球面上.
球心O是对称中心,一对对径点是关于球心O的对称点.三、球面是中心对称图形中心对称图形四、球面关于过球心的平面对称 如图,过球心的平面与球面交于一个大圆,球面关于过球心的平面是对称的. 球面上关于直径的旋转,关于球心、直径、过球心的平面的对称也叫做球面上的运动.
课堂小结1.球面是旋转曲面 2.球面关于它的任一直径对称 3.球面是中心对称图形4.球面关于过球心的平面对称谢谢指导!
同课章节目录
