苏教版高中选修3-3 3.1.3 球面坐标
文档属性
| 名称 | 苏教版高中选修3-3 3.1.3 球面坐标 |

|
|
| 格式 | zip | ||
| 文件大小 | 211.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 00:00:00 | ||
图片预览





文档简介
课件15张PPT。§ 3.1.3 球面坐标问题引入:
在平面上,我们可以通过平面直角坐标系
来确定点的位置,那么在球面上,我们如何确
定点的位置?
为了航海的目的,我们在球面上采用经纬度这样的坐标系.
子午线:
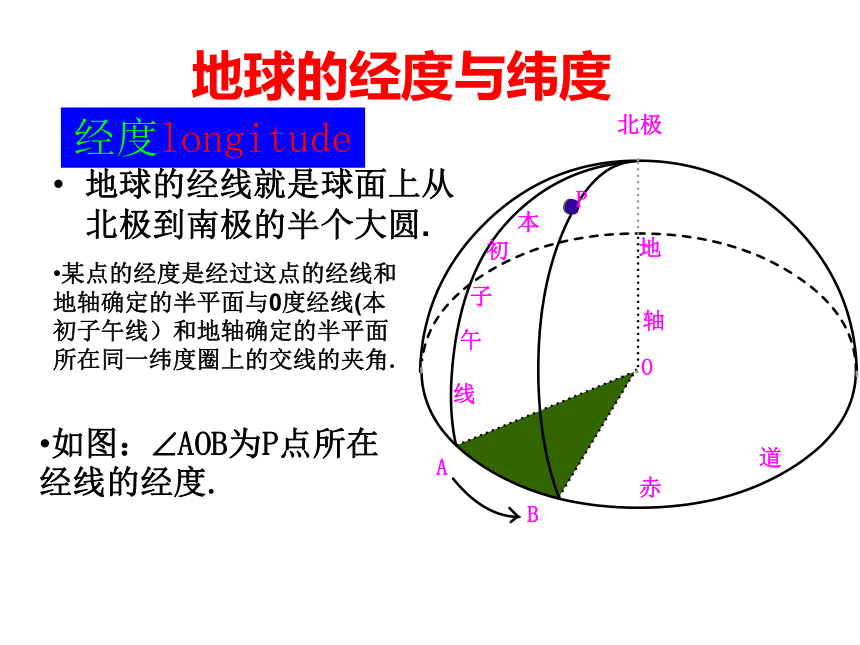
北极和南极是地球自转轴与球面的两个交点.赤道就是位于和极轴垂直的平面上的那个大圆.通过两极的任何大圆的一半(以两端为端点)都称为子午线(meridian),经过伦敦格林威治天文台的子午线称为格林威治子午线(或本初子午线、国际日期变更线).如图:?AOB为P点所在经线的经度.地球的经度与纬度某点的经度是经过这点的经线和地轴确定的半平面与0度经线(本初子午线)和地轴确定的半平面所在同一纬度圈上的交线的夹角.地球的经线就是球面上从北极到南极的半个大圆.经度longitude赤道是一个大圆,
其它的纬线都是小圆.某点的纬度就是经过这点的球半径与赤道面所成角的度数. 如图:
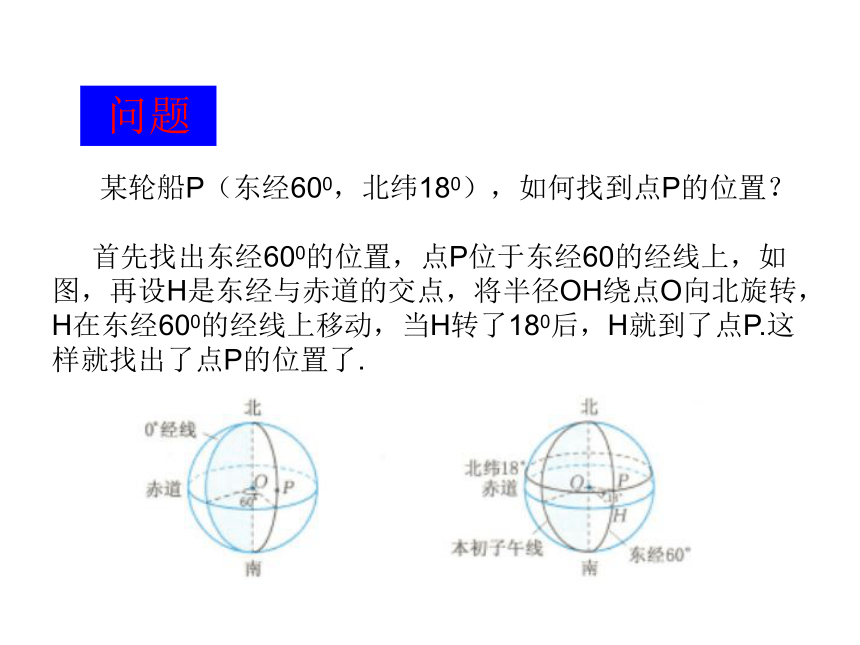
?AOP为P点纬度.纬度latitude 某轮船P(东经600,北纬180),如何找到点P的位置? 首先找出东经600的位置,点P位于东经60的经线上,如图,再设H是东经与赤道的交点,将半径OH绕点O向北旋转,H在东经600的经线上移动,当H转了180后,H就到了点P.这样就找出了点P的位置了.问题推广: 设Γ1 是赤道,S,N分别是南、北极, Γ2 是过S,N的大圆, Γ2 与Γ1 垂直,交于点C,D.Γ2右边半球叫东半球,左边半球叫西半球,N所在的上半球叫北半球,另一半球是南半球. 直线段OC与OM的夹角是θ,OM与OP的夹角是φ.θ,φ分别是点P的经度、纬度.
规定:
点P在东半球时,0°≤θ≤180°;
在西半球时,-180°≤θ≤0°.
点P在北半球时,0°≤φ≤90°;
在南半球时,-90°≤θ≤0°.
这样点P可以用两个参数(θ,φ)表示.球面上两点间的距离 平面上两点间的最短距离是连结这两点的线段的长度,而球的表面是曲面,球面上P、Q两点间的最短距离显然不是线段PQ的长度,那是什么呢? 在球面上,两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点间的球面距离. 两点的球面距离公式 =R∠AOB AB O例题:??例1.我国首都北京靠近北纬??,求北纬??纬线的长度.(地球半径约为6370km) 解答如图:
设纬线的圆心为D点,DP为纬线半径
∴ OD⊥DP
∵?DPO= ? POB=40°,
∴DP=OP×cos ? OPD
∴纬线长=2? × DP
= 2 ? × OP × cos40 °
≈2 × 3.14 × 6370 × 0.766 ≈30660(km)
设地球的半径为R,在北纬30 °纬线上有甲乙两地,它们的经度相差120 °,那么这两地的纬线的长为例2解:1:地球经、纬度的含义
2:球面上两点间的距离
重点:球面距离的求法及应用
课堂小结谢谢指导!
在平面上,我们可以通过平面直角坐标系
来确定点的位置,那么在球面上,我们如何确
定点的位置?
为了航海的目的,我们在球面上采用经纬度这样的坐标系.
子午线:
北极和南极是地球自转轴与球面的两个交点.赤道就是位于和极轴垂直的平面上的那个大圆.通过两极的任何大圆的一半(以两端为端点)都称为子午线(meridian),经过伦敦格林威治天文台的子午线称为格林威治子午线(或本初子午线、国际日期变更线).如图:?AOB为P点所在经线的经度.地球的经度与纬度某点的经度是经过这点的经线和地轴确定的半平面与0度经线(本初子午线)和地轴确定的半平面所在同一纬度圈上的交线的夹角.地球的经线就是球面上从北极到南极的半个大圆.经度longitude赤道是一个大圆,
其它的纬线都是小圆.某点的纬度就是经过这点的球半径与赤道面所成角的度数. 如图:
?AOP为P点纬度.纬度latitude 某轮船P(东经600,北纬180),如何找到点P的位置? 首先找出东经600的位置,点P位于东经60的经线上,如图,再设H是东经与赤道的交点,将半径OH绕点O向北旋转,H在东经600的经线上移动,当H转了180后,H就到了点P.这样就找出了点P的位置了.问题推广: 设Γ1 是赤道,S,N分别是南、北极, Γ2 是过S,N的大圆, Γ2 与Γ1 垂直,交于点C,D.Γ2右边半球叫东半球,左边半球叫西半球,N所在的上半球叫北半球,另一半球是南半球. 直线段OC与OM的夹角是θ,OM与OP的夹角是φ.θ,φ分别是点P的经度、纬度.
规定:
点P在东半球时,0°≤θ≤180°;
在西半球时,-180°≤θ≤0°.
点P在北半球时,0°≤φ≤90°;
在南半球时,-90°≤θ≤0°.
这样点P可以用两个参数(θ,φ)表示.球面上两点间的距离 平面上两点间的最短距离是连结这两点的线段的长度,而球的表面是曲面,球面上P、Q两点间的最短距离显然不是线段PQ的长度,那是什么呢? 在球面上,两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点间的球面距离. 两点的球面距离公式 =R∠AOB AB O例题:??例1.我国首都北京靠近北纬??,求北纬??纬线的长度.(地球半径约为6370km) 解答如图:
设纬线的圆心为D点,DP为纬线半径
∴ OD⊥DP
∵?DPO= ? POB=40°,
∴DP=OP×cos ? OPD
∴纬线长=2? × DP
= 2 ? × OP × cos40 °
≈2 × 3.14 × 6370 × 0.766 ≈30660(km)
设地球的半径为R,在北纬30 °纬线上有甲乙两地,它们的经度相差120 °,那么这两地的纬线的长为例2解:1:地球经、纬度的含义
2:球面上两点间的距离
重点:球面距离的求法及应用
课堂小结谢谢指导!
同课章节目录
