苏教版高中选修3-3 3.2 球面上的直线
文档属性
| 名称 | 苏教版高中选修3-3 3.2 球面上的直线 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 00:00:00 | ||
图片预览





文档简介
课件17张PPT。§ 3.2 球面上的直线 空间或平面内的两点决定一条线段,这条线
段是连结这两点的最短曲线,那么对于球面上的
两点,连结这两点的什么样的球面曲线最短?
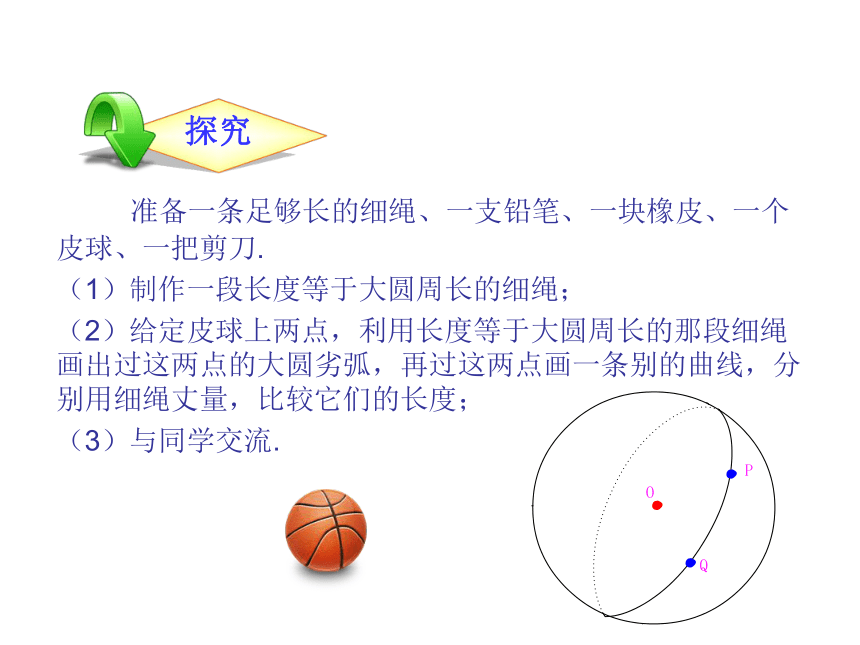
准备一条足够长的细绳、一支铅笔、一块橡皮、一个皮球、一把剪刀.
(1)制作一段长度等于大圆周长的细绳;
(2)给定皮球上两点,利用长度等于大圆周长的那段细绳画出过这两点的大圆劣弧,再过这两点画一条别的曲线,分别用细绳丈量,比较它们的长度;
(3)与同学交流. 如图,从北京到纽约,选择什么线路才能使路程最短?是从北京乘飞机向东飞?还是经过北极地域?
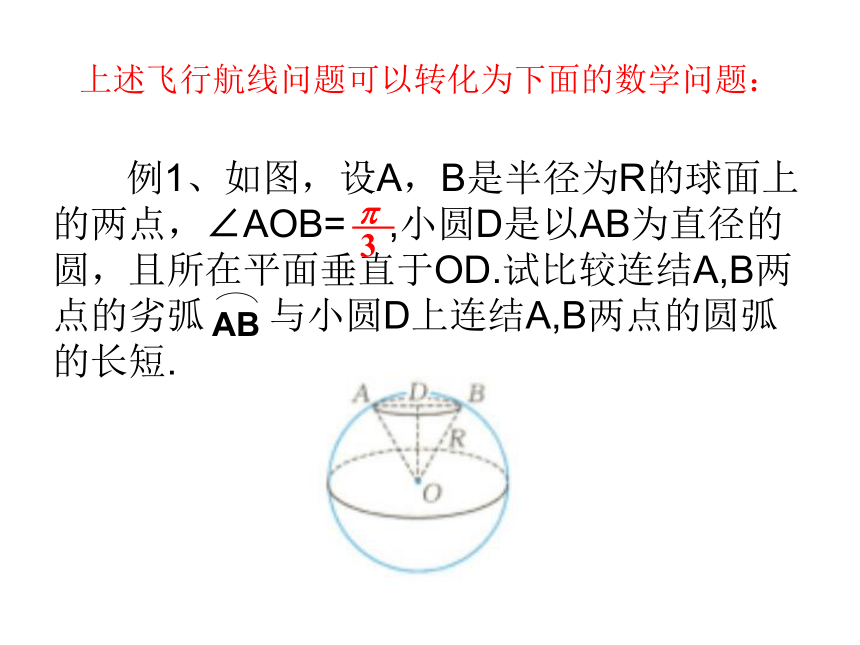
上述飞行航线问题可以转化为下面的数学问题: 例1、如图,设A,B是半径为R的球面上的两点,∠AOB= ,小圆D是以AB为直径的圆,且所在平面垂直于OD.试比较连结A,B两点的劣弧 与小圆D上连结A,B两点的圆弧的长短.解:A,O,B构成一个等边三角形,连结A,B两点的劣弧 = R.线段AB长是R,因此小圆D的半圆周长是 R.由于 R 解:A,O,B构成一个等边三角形,连结A,B两点的劣弧 = R.线段AB长是R,因此小圆D的半圆周长是 R.由于 R< R,所以连结A,B的劣弧比连结A,B两点的这一段小圆弧短.
即从A点出发向东飞行到点B,与经过北极沿着大圆弧飞行到点B的路线相比,后一种飞法要好.地球半径R=6400千米,这时行程缩短了
R - R= R≈3350(千米) 如图,过线段AB的圆很多,把这些圆都放在同一平面内,半径较大的圆上由A,B决定的同一侧的弧较短,而且半径越大,连结A,B的劣弧与弦AB越接近.因为地球近似于球体,在地面两点之间的最短航线应该是大圆的一段劣弧,沿它飞行的航线叫做直航线.
对于球面上的一对对径点,
连结它们的大圆弧很多,它们
的长度都是πR. 结论球面三角形 设A,B,C是球面上不在同一个大圆上的三点,它们两两不是对径点,我们把这三点及连结它们的大圆的三条劣弧 , , 构成的图形叫做球面三角形(spherical triangle),记作ΔABC.三边的弧长叫球面三角形的三边长. 例2 是否存在球面ΔABC,使A+B=π或A+B>π?
解:如图(1),OC⊥OA,OC⊥OB,则 , 与 都垂直,A=B= , 自然,也可以取球面ΔABC,使此三角形三边所在平面两两垂直,即OC⊥OA,OC⊥OB,
OA⊥OB,这时球面ΔABC的三个内角都是直角.如图(2),球面ΔA'BC是三内角都是 的三角形,在 上取点A,过A作大圆交 于C,使得∠BAC> =∠ABD.这样的球面ΔABC满足A+B=π. 球面ΔABC的任意两边之和大于第三边
定理2.1证 我们以证明 为例,由于
因此 成立的充要条件是∠AOC+∠COB>∠AOB.
证明如下:
不妨设∠AOB>∠AOC.如图,考虑四面体
O-ABC,在AB上取点D,使∠AOD=∠AOC,
在线段OC上取点C',使OC'=OD,
于是ΔAOD与ΔAOC'全等,AD=AC'.
在ΔABC',
AB因而 DB在ΔODB与ΔOC'B中,OD=OC',OB=OB,
于是从 DB可得 ∠COB=∠C'OB>∠DOB.
所以 ∠AOC+∠COB>∠AOB.定理2.2 设A,B不是对径点,则在连结A,B的所有可求长曲线中,大圆劣弧是最短的,且最短曲线只有这一条. 球面上的曲线有的可求长度,也有不可求长度.我们有 球面直线:球面上的大圆是球面上的直线.大圆弧是球面上的线段.
如果A,B是球面上的一对对径点,在连结A,B的所有可求长曲线中,半大圆是最短的,连结A,B的半大圆有许多,它们的长相同,都是最短曲线.
球面距离:过圆上不是对径点的A,B的大圆上劣弧的长.
极点:设大圆Γ 所在平面垂直与AA',则 Γ与Γ1,Γ2都垂直,称A,A'是Γ的两个极点.
定义: 平面上到定点距离等于定长的点的轨迹是圆.
球面上到定点的距离等于r( ,且是一个正常数)的点的轨迹是圆.这个圆是一个平面与球面的交线.它的半径是 ,圆周长是 .1、球面三角形的概念;
2、球面直线、球面距离的概念;
3、定理2.1
4、定理2.2
谢谢指导!
段是连结这两点的最短曲线,那么对于球面上的
两点,连结这两点的什么样的球面曲线最短?
准备一条足够长的细绳、一支铅笔、一块橡皮、一个皮球、一把剪刀.
(1)制作一段长度等于大圆周长的细绳;
(2)给定皮球上两点,利用长度等于大圆周长的那段细绳画出过这两点的大圆劣弧,再过这两点画一条别的曲线,分别用细绳丈量,比较它们的长度;
(3)与同学交流. 如图,从北京到纽约,选择什么线路才能使路程最短?是从北京乘飞机向东飞?还是经过北极地域?
上述飞行航线问题可以转化为下面的数学问题: 例1、如图,设A,B是半径为R的球面上的两点,∠AOB= ,小圆D是以AB为直径的圆,且所在平面垂直于OD.试比较连结A,B两点的劣弧 与小圆D上连结A,B两点的圆弧的长短.解:A,O,B构成一个等边三角形,连结A,B两点的劣弧 = R.线段AB长是R,因此小圆D的半圆周长是 R.由于 R 解:A,O,B构成一个等边三角形,连结A,B两点的劣弧 = R.线段AB长是R,因此小圆D的半圆周长是 R.由于 R< R,所以连结A,B的劣弧比连结A,B两点的这一段小圆弧短.
即从A点出发向东飞行到点B,与经过北极沿着大圆弧飞行到点B的路线相比,后一种飞法要好.地球半径R=6400千米,这时行程缩短了
R - R= R≈3350(千米) 如图,过线段AB的圆很多,把这些圆都放在同一平面内,半径较大的圆上由A,B决定的同一侧的弧较短,而且半径越大,连结A,B的劣弧与弦AB越接近.因为地球近似于球体,在地面两点之间的最短航线应该是大圆的一段劣弧,沿它飞行的航线叫做直航线.
对于球面上的一对对径点,
连结它们的大圆弧很多,它们
的长度都是πR. 结论球面三角形 设A,B,C是球面上不在同一个大圆上的三点,它们两两不是对径点,我们把这三点及连结它们的大圆的三条劣弧 , , 构成的图形叫做球面三角形(spherical triangle),记作ΔABC.三边的弧长叫球面三角形的三边长. 例2 是否存在球面ΔABC,使A+B=π或A+B>π?
解:如图(1),OC⊥OA,OC⊥OB,则 , 与 都垂直,A=B= , 自然,也可以取球面ΔABC,使此三角形三边所在平面两两垂直,即OC⊥OA,OC⊥OB,
OA⊥OB,这时球面ΔABC的三个内角都是直角.如图(2),球面ΔA'BC是三内角都是 的三角形,在 上取点A,过A作大圆交 于C,使得∠BAC> =∠ABD.这样的球面ΔABC满足A+B=π. 球面ΔABC的任意两边之和大于第三边
定理2.1证 我们以证明 为例,由于
因此 成立的充要条件是∠AOC+∠COB>∠AOB.
证明如下:
不妨设∠AOB>∠AOC.如图,考虑四面体
O-ABC,在AB上取点D,使∠AOD=∠AOC,
在线段OC上取点C',使OC'=OD,
于是ΔAOD与ΔAOC'全等,AD=AC'.
在ΔABC',
AB
于是从 DB
所以 ∠AOC+∠COB>∠AOB.定理2.2 设A,B不是对径点,则在连结A,B的所有可求长曲线中,大圆劣弧是最短的,且最短曲线只有这一条. 球面上的曲线有的可求长度,也有不可求长度.我们有 球面直线:球面上的大圆是球面上的直线.大圆弧是球面上的线段.
如果A,B是球面上的一对对径点,在连结A,B的所有可求长曲线中,半大圆是最短的,连结A,B的半大圆有许多,它们的长相同,都是最短曲线.
球面距离:过圆上不是对径点的A,B的大圆上劣弧的长.
极点:设大圆Γ 所在平面垂直与AA',则 Γ与Γ1,Γ2都垂直,称A,A'是Γ的两个极点.
定义: 平面上到定点距离等于定长的点的轨迹是圆.
球面上到定点的距离等于r( ,且是一个正常数)的点的轨迹是圆.这个圆是一个平面与球面的交线.它的半径是 ,圆周长是 .1、球面三角形的概念;
2、球面直线、球面距离的概念;
3、定理2.1
4、定理2.2
谢谢指导!
同课章节目录
