苏教版高中选修3-3 3.3.2 欧拉公式
文档属性
| 名称 | 苏教版高中选修3-3 3.3.2 欧拉公式 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 00:00:00 | ||
图片预览






文档简介
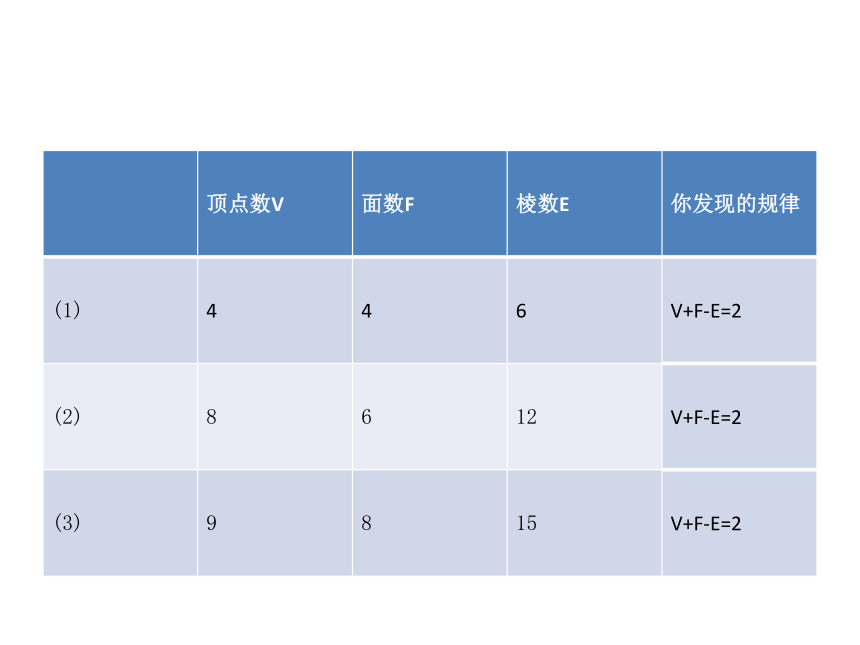
课件19张PPT。§3.3.2欧拉公式探索研究有三个多面体,请找出它们的顶点数(vertex)V、面数(face)F、 棱数(edge)E,填入下表,并观察V、F、E之间的规律,归纳出你发现的规律. 平面三角形可以推广到多边形,那么,球面三角形能推广到球面多边形吗?
设A1,A2,...An是球面上n个点,任意相邻三点(如A1,A2,A3;An,A1,A2)不在一个大圆上.依次用劣弧或取定的半大圆(当相邻两点为对径点时)连结相邻两点,得球面上线段弧 .这些线段在内部不相交,它们所形成的图形叫做球面多边形(spherical polygon).球面多边形 进一步,如果多边形A1A2...An总在它的每一边 所在大圆划分球面所成的一个半球面内,称此多边形是凸多边形.
如:球面二角形,球面三角形都是球面凸多边形. 把n边形分成(n-2)个球面三角形,由定理3.1可得:定理3.2 单位曲面上n边形A1A2...An的面积是
A1+A2+...+An-(n-2)π. 凸多面体是四面体、立方体等图形的自然推广,我们以V,E,F表示多面体顶点数、棱数、面数.
例如,对于四面体,有V=4,E=6,F=4,
对于平行六面体,有V=8,E=12,F=6.
因此,两种情况都有V-E+F=2.
定理应用——证明凸多面体的欧拉公式定理3.3(欧拉公式) 对于任一个凸多面体,都有
V - E + F = 2,
其中V,E,F分别表示这个多面体的顶点数,棱数,面数.证 以凸多面体内一点O为球心作一个球面,使得此凸多面体完全在球面内.由于要证明的公式与凸多面体的大小无关,不妨设R=1.
设想在O处有一光源,它把多面体表面上的点一一投影到球面上.不难知道,这一映射把多面体的棱变成球面上一条劣弧,因此它把多面体的每一个面投影成球面上一个多边形,多面体的两个面的公共棱成为球面上多边形的公共边.
这样我们从凸多面体得到球面的一个剖分:球面由球面多边形拼成.球面多边形的个数、总边数、顶点数分别是多面体的面数F、棱数E、顶点数V.
图中画出了正八面体的
情形.这些多边形分别记为D1,
D2,...DF.球面多边形Di的面积
为Si,边数记为Ei,顶点数也是Ei,其内角和记为Ai.由于球面多边形Di的每一条边也是另一个多边形的一条边(i=1,2,...F),因此
E1+E2+...+EF=2E.
显然, S1+S2+...+SF=4π.
另一方面,所有球面多边形的内角和是2πV,即
A1+A2+...+AF=2πV.
由定理3.2得S1=A1-(E1-2)π,
S2=A2-(E2-2)π,
...
SF=AF-(EF-2)π,
两边相加得,
S1+S2+...+SF=A1+A2+...+AF-(E1+E2+...+EF)π+2πF.
于是 4π=2πV-2πE+2πF,
即 V-E+F=2 用欧拉公式可以证明正多面体有五种,分别是正四面体、正六面体、正八面体、正十二面体与正二十面体,它们分别是用正三角形、正方形、正三角形、正五边形与正三角形拼起来的.例 观察下面的球面三角剖分,记录它们的顶点数V,三角形边数E和三角形个数F,说明它们满足什么关系?解 在左图中,顶点为A、B、C、D,顶点数V=4,
三角形的边为AB、AC、AD、BC、BD、CD,边数E=6,
三角形为ABC、ABD、ACD、BCD,三角形个数F=4,
所以 ;
在中图中,顶点为A、B、C、D、E、F,顶点数V=6,
三角形的边为AB、AC、AD、AE,FB、FC、FD、FE、BC、BE、CD、ED,边数E=12,
三角形为ABC、ABE、ACD、ADE,FBC、FBE、FCD、FDE,三角形个数F=8,
所以 ;
在右图中,顶点为A、B、C、D、E、F、G、H,顶点数V=8,
三角形的边为AB、AC、AH、HD、AE、CH、HE,FG、GB、FC、FD、FE、BC、BE、CD、ED、CG、GE,边数E=18,
三角形为ABC、ABE、ACH、CHD、AHE、HED,FGC、GCB、FGE、GEB、FCD、FDE,三角形个数F=12,
所以 .足球多面体假设足球多面体共有 x个五边形,y个六边形,那么
联立上述方程我们就可以解出所有未知数。 1.一个凸多面体的棱数为30,面数为12,则它的各面多边形的内角总和为( B )
A.5400° B.6480°
C.7200° D.7920°【解】由欧拉公式V=E-F+2=20∴内角总和为6480°,选B例题: 2.一个正多面体的每个面都是三角形,从每个顶点引出的棱都有4条,则该正多面体为( C )
A.正四面体 B.正六面体
C.正八面体 D.正十二面体解:认识欧拉数学奇才欧拉
欧拉---瑞士人(Euler,L. 1707---1783);
欧拉---16 岁获得硕士学位;
欧拉---数学史上“高产”的数学家。在世发表论文700多篇,
去世后还留下100多篇待发表;
欧拉---首先使用f(x)表示函数,用e表示自然对数的底,用a、
b、c 表示△ABC,用∑表示求和,用i表示虚数单位等;
欧拉---目前数学中有欧拉公式、欧拉常数、欧拉猜想、欧拉
方法、欧拉方程、欧拉定理。谢谢指导!
设A1,A2,...An是球面上n个点,任意相邻三点(如A1,A2,A3;An,A1,A2)不在一个大圆上.依次用劣弧或取定的半大圆(当相邻两点为对径点时)连结相邻两点,得球面上线段弧 .这些线段在内部不相交,它们所形成的图形叫做球面多边形(spherical polygon).球面多边形 进一步,如果多边形A1A2...An总在它的每一边 所在大圆划分球面所成的一个半球面内,称此多边形是凸多边形.
如:球面二角形,球面三角形都是球面凸多边形. 把n边形分成(n-2)个球面三角形,由定理3.1可得:定理3.2 单位曲面上n边形A1A2...An的面积是
A1+A2+...+An-(n-2)π. 凸多面体是四面体、立方体等图形的自然推广,我们以V,E,F表示多面体顶点数、棱数、面数.
例如,对于四面体,有V=4,E=6,F=4,
对于平行六面体,有V=8,E=12,F=6.
因此,两种情况都有V-E+F=2.
定理应用——证明凸多面体的欧拉公式定理3.3(欧拉公式) 对于任一个凸多面体,都有
V - E + F = 2,
其中V,E,F分别表示这个多面体的顶点数,棱数,面数.证 以凸多面体内一点O为球心作一个球面,使得此凸多面体完全在球面内.由于要证明的公式与凸多面体的大小无关,不妨设R=1.
设想在O处有一光源,它把多面体表面上的点一一投影到球面上.不难知道,这一映射把多面体的棱变成球面上一条劣弧,因此它把多面体的每一个面投影成球面上一个多边形,多面体的两个面的公共棱成为球面上多边形的公共边.
这样我们从凸多面体得到球面的一个剖分:球面由球面多边形拼成.球面多边形的个数、总边数、顶点数分别是多面体的面数F、棱数E、顶点数V.
图中画出了正八面体的
情形.这些多边形分别记为D1,
D2,...DF.球面多边形Di的面积
为Si,边数记为Ei,顶点数也是Ei,其内角和记为Ai.由于球面多边形Di的每一条边也是另一个多边形的一条边(i=1,2,...F),因此
E1+E2+...+EF=2E.
显然, S1+S2+...+SF=4π.
另一方面,所有球面多边形的内角和是2πV,即
A1+A2+...+AF=2πV.
由定理3.2得S1=A1-(E1-2)π,
S2=A2-(E2-2)π,
...
SF=AF-(EF-2)π,
两边相加得,
S1+S2+...+SF=A1+A2+...+AF-(E1+E2+...+EF)π+2πF.
于是 4π=2πV-2πE+2πF,
即 V-E+F=2 用欧拉公式可以证明正多面体有五种,分别是正四面体、正六面体、正八面体、正十二面体与正二十面体,它们分别是用正三角形、正方形、正三角形、正五边形与正三角形拼起来的.例 观察下面的球面三角剖分,记录它们的顶点数V,三角形边数E和三角形个数F,说明它们满足什么关系?解 在左图中,顶点为A、B、C、D,顶点数V=4,
三角形的边为AB、AC、AD、BC、BD、CD,边数E=6,
三角形为ABC、ABD、ACD、BCD,三角形个数F=4,
所以 ;
在中图中,顶点为A、B、C、D、E、F,顶点数V=6,
三角形的边为AB、AC、AD、AE,FB、FC、FD、FE、BC、BE、CD、ED,边数E=12,
三角形为ABC、ABE、ACD、ADE,FBC、FBE、FCD、FDE,三角形个数F=8,
所以 ;
在右图中,顶点为A、B、C、D、E、F、G、H,顶点数V=8,
三角形的边为AB、AC、AH、HD、AE、CH、HE,FG、GB、FC、FD、FE、BC、BE、CD、ED、CG、GE,边数E=18,
三角形为ABC、ABE、ACH、CHD、AHE、HED,FGC、GCB、FGE、GEB、FCD、FDE,三角形个数F=12,
所以 .足球多面体假设足球多面体共有 x个五边形,y个六边形,那么
联立上述方程我们就可以解出所有未知数。 1.一个凸多面体的棱数为30,面数为12,则它的各面多边形的内角总和为( B )
A.5400° B.6480°
C.7200° D.7920°【解】由欧拉公式V=E-F+2=20∴内角总和为6480°,选B例题: 2.一个正多面体的每个面都是三角形,从每个顶点引出的棱都有4条,则该正多面体为( C )
A.正四面体 B.正六面体
C.正八面体 D.正十二面体解:认识欧拉数学奇才欧拉
欧拉---瑞士人(Euler,L. 1707---1783);
欧拉---16 岁获得硕士学位;
欧拉---数学史上“高产”的数学家。在世发表论文700多篇,
去世后还留下100多篇待发表;
欧拉---首先使用f(x)表示函数,用e表示自然对数的底,用a、
b、c 表示△ABC,用∑表示求和,用i表示虚数单位等;
欧拉---目前数学中有欧拉公式、欧拉常数、欧拉猜想、欧拉
方法、欧拉方程、欧拉定理。谢谢指导!
同课章节目录
