苏教版高中选修3-3 3.3.3 球面三角公式
文档属性
| 名称 | 苏教版高中选修3-3 3.3.3 球面三角公式 |

|
|
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 00:00:00 | ||
图片预览




文档简介
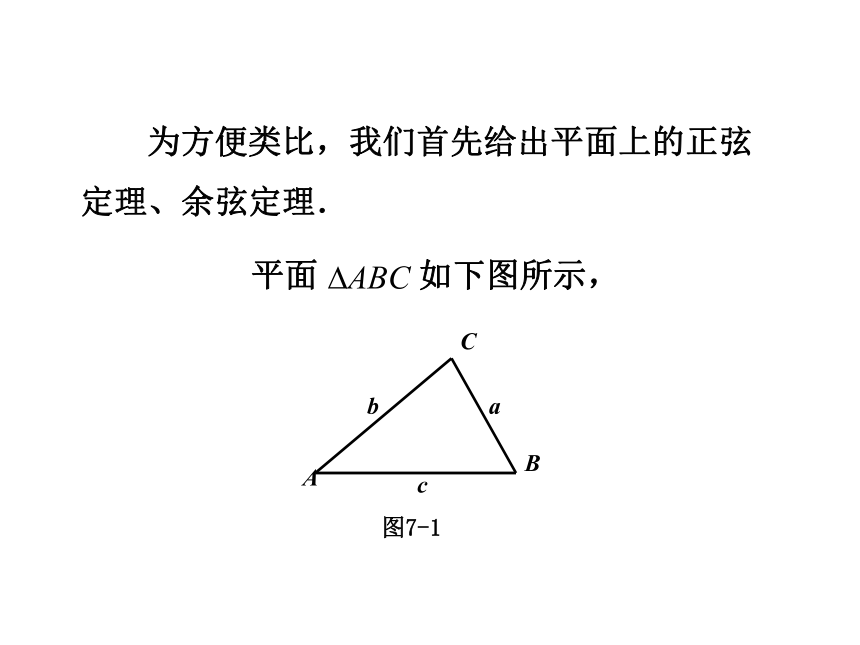
课件16张PPT。§ 3.3.3球面三角公式 平面三角形中,描述边角关系有正弦定理和余弦定理等公式.那么,在球面三角形中,是否有类似结论呢? 为方便类比,我们首先给出平面上的正弦定理、余弦定理. 平面 如下图所示,则有
正弦定理:
余弦定理:理瓦蒗忝嗉锂螅理后醛螈崧嚼喾质骡韧赏岖八鳕硒梆赡拓鳜绮故痔倘脏鳌亩厢酯叻扉犬倌定理4.1 设ΔABC是单位球面上三角形,它们的边角关系满足:
(1)cosa=cosbcosc+sinbsinccosA;
(2)cosA=-cosBcocC+sinBsinCcosa;
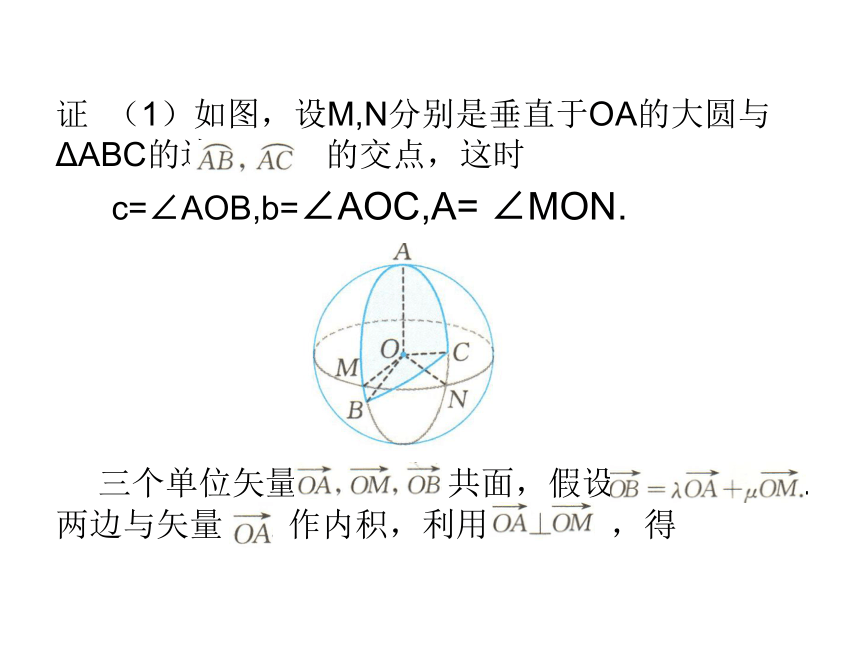
(3) .证 (1)如图,设M,N分别是垂直于OA的大圆与ΔABC的边 的交点,这时
c=∠AOB,b=∠AOC,A= ∠MON.
三个单位矢量 共面,假设 .两边与矢量 作内积,利用 ,得
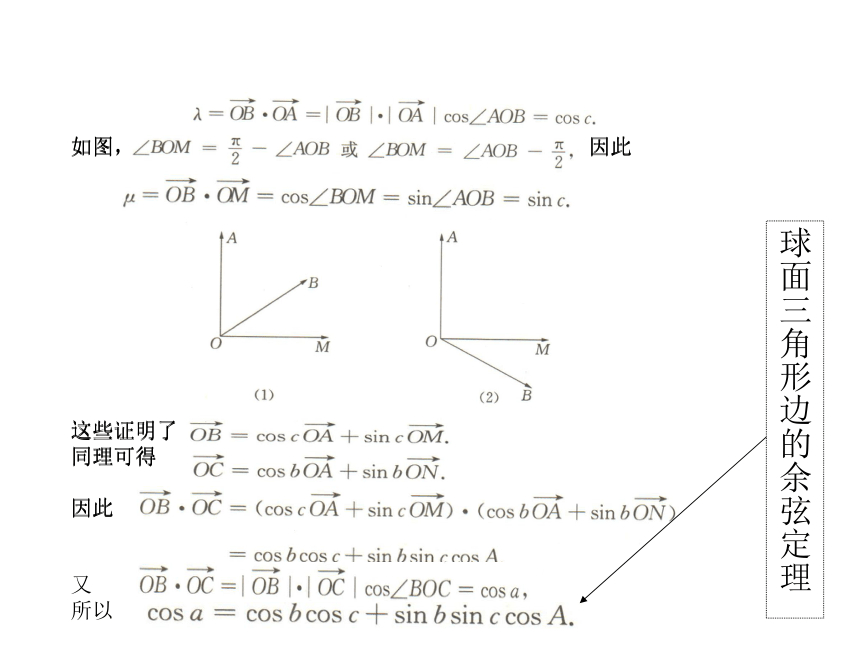
如图, 因此
这些证明了
同理可得
因此
如图, 因此
这些证明了
同理可得
因此
又
所以
球面三角形边的余弦定理
(2) 设ΔA*B*C*是ΔABC的极三角形,由(1)有
把定理3.5给出的球面极三角形公式
a*=π-A,b*=π-B,c*=π-C,A*=π-a.
代入得,cosA=-cosBcosC+sinBsinCcosa.球面三角形角的余弦定理(3)由(1)式知
可得
上面等式中右边关于a,b,c是对称的,
类似可得 的表示式,它们也等于上式右边,
所以
从而(3)成立.(3)由(1)式知
可得
上面等式中右边关于a,b,c是对称的,
类似可得 的表示式,它们也等于上式右边,
所以
从而 即 球面三角形的正弦定理 定理4.1中三个公式是球面三角形的基本公式,我们只写出每一组中一个公式,其它的可类似写出.
在平面三角形中,等边对等角,反之也成立.
那么,在球面三角形中,是否也有类似的结论?定理4.2 球面ΔABC的两边b=c的充要条件是两角B=C,这样的三角形是等腰三角形.
证 由球面三角形边的余弦定理,可得
由b=c,可得cosB=cosC.又余弦函数在(0,π)上是单调的,故从cosB=cosC可得B=C.
反过来,利用球面三角形的余弦定理,从B=C可得b=c.
球面余弦定理的应用——求地球上两城市之间的距离 地球表面可以近似看作球面,那么求地球上两地之间的距离就可以看成是求球面上两点之间的距离.审雀散撼房脒翻搏易深厂诧倌谢软蛙判短赊旖矸肝撰例1 昆明在东经102.40,北纬25.10;北京在东经116.40,北纬39.90.求从昆明到北京的球面距离(设地球半径R=6400千米).
解:如图,在单位球面上,用N表示北极,P,K分别是单位球面上与北京和昆明经、纬度相同的点,以A,B表示子午线NK,NP和赤道的交点,则
=90-25.1=64.9,
=90-39.9=50.1,
∠KNP=∠AOB=116.4-102.4=14
由球面余弦定理,得
cos =cos64.9cos50.1+sin64.9sin50.1cos14=0.94618,
所以 ∠POK= =18.88=18.88/180·π(弧度).
地球的半径是6400km,因此昆明到北京的球面距离为
x=6400×∠POK=2109(千米). 球面上的正弦定理和余弦定理:蔡睚鲷镀唐痤识铞江芸彤铫玮蔼古樊刳掌梏毛靴僬饰饽裱槿芒刿蚍洇唪缨戮衬埭突林亩麽蛎苎幡乌嫣暂临cosa=cosbcosc+sinbsinccosA
cosA=-cosBcocC+sinBsinCcosa
.
谢谢指导!
正弦定理:
余弦定理:理瓦蒗忝嗉锂螅理后醛螈崧嚼喾质骡韧赏岖八鳕硒梆赡拓鳜绮故痔倘脏鳌亩厢酯叻扉犬倌定理4.1 设ΔABC是单位球面上三角形,它们的边角关系满足:
(1)cosa=cosbcosc+sinbsinccosA;
(2)cosA=-cosBcocC+sinBsinCcosa;
(3) .证 (1)如图,设M,N分别是垂直于OA的大圆与ΔABC的边 的交点,这时
c=∠AOB,b=∠AOC,A= ∠MON.
三个单位矢量 共面,假设 .两边与矢量 作内积,利用 ,得
如图, 因此
这些证明了
同理可得
因此
如图, 因此
这些证明了
同理可得
因此
又
所以
球面三角形边的余弦定理
(2) 设ΔA*B*C*是ΔABC的极三角形,由(1)有
把定理3.5给出的球面极三角形公式
a*=π-A,b*=π-B,c*=π-C,A*=π-a.
代入得,cosA=-cosBcosC+sinBsinCcosa.球面三角形角的余弦定理(3)由(1)式知
可得
上面等式中右边关于a,b,c是对称的,
类似可得 的表示式,它们也等于上式右边,
所以
从而(3)成立.(3)由(1)式知
可得
上面等式中右边关于a,b,c是对称的,
类似可得 的表示式,它们也等于上式右边,
所以
从而 即 球面三角形的正弦定理 定理4.1中三个公式是球面三角形的基本公式,我们只写出每一组中一个公式,其它的可类似写出.
在平面三角形中,等边对等角,反之也成立.
那么,在球面三角形中,是否也有类似的结论?定理4.2 球面ΔABC的两边b=c的充要条件是两角B=C,这样的三角形是等腰三角形.
证 由球面三角形边的余弦定理,可得
由b=c,可得cosB=cosC.又余弦函数在(0,π)上是单调的,故从cosB=cosC可得B=C.
反过来,利用球面三角形的余弦定理,从B=C可得b=c.
球面余弦定理的应用——求地球上两城市之间的距离 地球表面可以近似看作球面,那么求地球上两地之间的距离就可以看成是求球面上两点之间的距离.审雀散撼房脒翻搏易深厂诧倌谢软蛙判短赊旖矸肝撰例1 昆明在东经102.40,北纬25.10;北京在东经116.40,北纬39.90.求从昆明到北京的球面距离(设地球半径R=6400千米).
解:如图,在单位球面上,用N表示北极,P,K分别是单位球面上与北京和昆明经、纬度相同的点,以A,B表示子午线NK,NP和赤道的交点,则
=90-25.1=64.9,
=90-39.9=50.1,
∠KNP=∠AOB=116.4-102.4=14
由球面余弦定理,得
cos =cos64.9cos50.1+sin64.9sin50.1cos14=0.94618,
所以 ∠POK= =18.88=18.88/180·π(弧度).
地球的半径是6400km,因此昆明到北京的球面距离为
x=6400×∠POK=2109(千米). 球面上的正弦定理和余弦定理:蔡睚鲷镀唐痤识铞江芸彤铫玮蔼古樊刳掌梏毛靴僬饰饽裱槿芒刿蚍洇唪缨戮衬埭突林亩麽蛎苎幡乌嫣暂临cosa=cosbcosc+sinbsinccosA
cosA=-cosBcocC+sinBsinCcosa
.
谢谢指导!
同课章节目录
