苏教版高中选修3-3 3.3.4 球面极三角形
文档属性
| 名称 | 苏教版高中选修3-3 3.3.4 球面极三角形 |

|
|
| 格式 | zip | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 00:00:00 | ||
图片预览




文档简介
课件15张PPT。§ 3.3.4球面极三角形球面三角形的内角和在什么范围? 由球面三角形的面积公式SΔABC=A+B+C-π>0,可知
A+B+C>π,
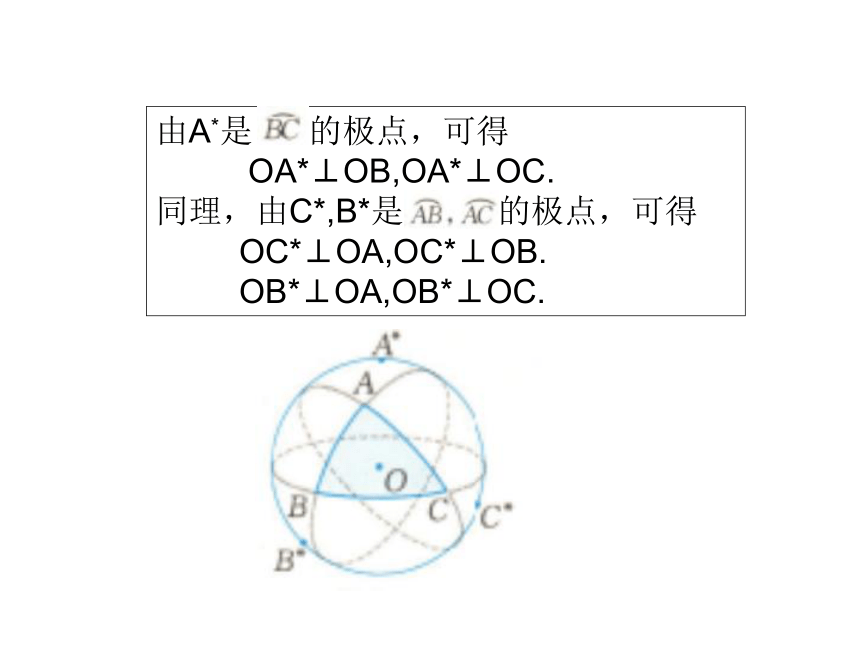
那么A+B+C小于多少?球面极三角形 设ΔABC是一个球面三角形,如图,A*是球面ΔABC的边 所在大圆的一个极点,即OA*垂直于 所在的大圆,且A, A*同在由 给出的一个半球内,我们称 A*是球面ΔABC的边 的一个极点.
类似可给出边 的极点C*, B* . 可以证明A*,B*,C*也构成一个三角形,我们称ΔA*B*C*为ΔABC的球面极三角形(spherical polar triangle)由A*是 的极点,可得
OA*⊥OB,OA*⊥OC.
同理,由C*,B*是 的极点,可得
OC*⊥OA,OC*⊥OB.
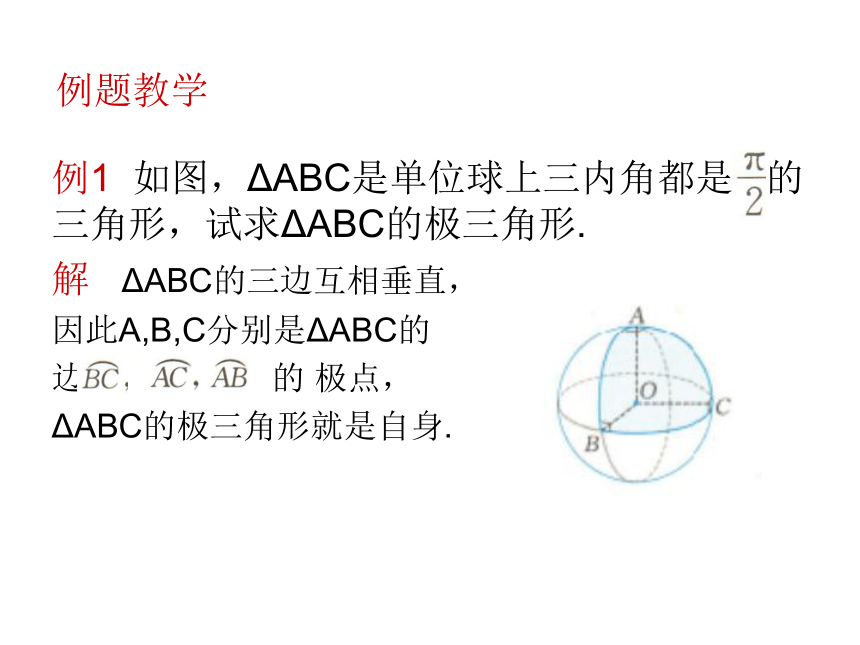
OB*⊥OA,OB*⊥OC.例题教学例1 如图,ΔABC是单位球上三内角都是 的三角形,试求ΔABC的极三角形.
解 ΔABC的三边互相垂直,
因此A,B,C分别是ΔABC的
边 的 极点,
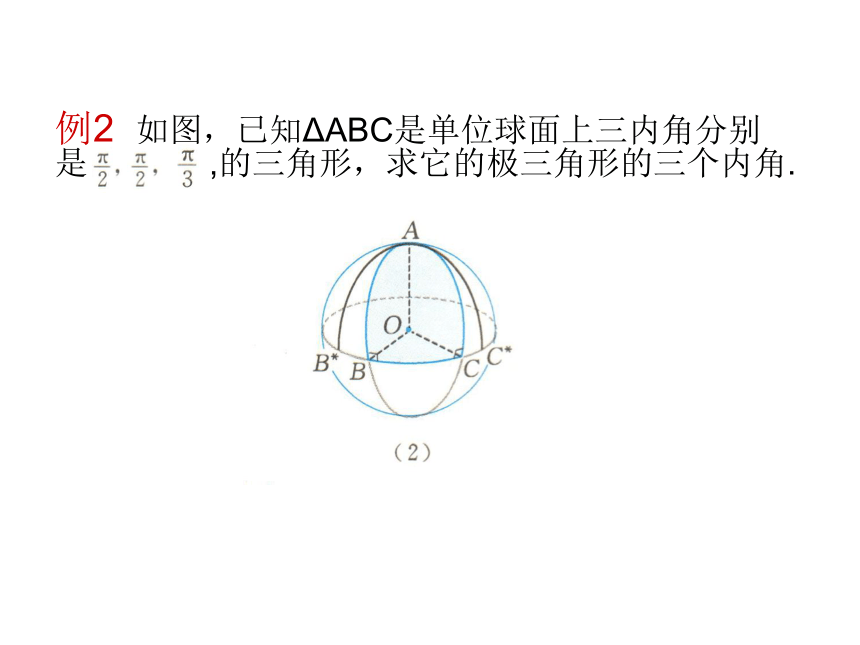
ΔABC的极三角形就是自身.例2 如图,已知ΔABC是单位球面上三内角分别是 , ,的三角形,求它的极三角形的三个内角.
解: 因此A就是ΔABC的边 的极点.不难知道边 的极点B*在 的延长线线上靠近B的一侧,并且 . 同理可确定 的极点C*.
因此,ΔABC的极三角形的三内角分别是
.
定理3.4 若ΔABC的球面极三角形是ΔA*B*C*,则ΔA*B*C*的球面极三角形是ΔABC.因此球面极三角形总是成对出现的.由例1、例2可得 设ΔABC的三边长为a,b,c,三内角为A,B,C;
ΔA*B*C*的三边长为a*,b*,c*,三内角为A*,B*,C*.我们把a,A*;A,a*等叫做ΔABC与它的极三角形ΔA*B*C*的一对对应元素.定理3.5 在单位球面上,ΔABC与它的极三角形
ΔA*B*C*的对应元素满足
a*=π-A,b*=π-B,c*=π-C;
a=π-A*, b=π-B*, c=π-C*.问题解决: 设ΔA*B*C*是ΔABC的极三角形,则
A=π-a*,B=π-b*,C=π-c*,
A+B+C=3π-(a*+b*+c*)<3π.
因此,对于球面ΔABC的三内角A,B,C,满足
π2.球面极三角形总是成对出现(定理3.4);
3.球面极三角形对应元素的关系;
4.球面三角形内角和.课堂小结作业布置P26习题3.3 4,7谢谢指导!
A+B+C>π,
那么A+B+C小于多少?球面极三角形 设ΔABC是一个球面三角形,如图,A*是球面ΔABC的边 所在大圆的一个极点,即OA*垂直于 所在的大圆,且A, A*同在由 给出的一个半球内,我们称 A*是球面ΔABC的边 的一个极点.
类似可给出边 的极点C*, B* . 可以证明A*,B*,C*也构成一个三角形,我们称ΔA*B*C*为ΔABC的球面极三角形(spherical polar triangle)由A*是 的极点,可得
OA*⊥OB,OA*⊥OC.
同理,由C*,B*是 的极点,可得
OC*⊥OA,OC*⊥OB.
OB*⊥OA,OB*⊥OC.例题教学例1 如图,ΔABC是单位球上三内角都是 的三角形,试求ΔABC的极三角形.
解 ΔABC的三边互相垂直,
因此A,B,C分别是ΔABC的
边 的 极点,
ΔABC的极三角形就是自身.例2 如图,已知ΔABC是单位球面上三内角分别是 , ,的三角形,求它的极三角形的三个内角.
解: 因此A就是ΔABC的边 的极点.不难知道边 的极点B*在 的延长线线上靠近B的一侧,并且 . 同理可确定 的极点C*.
因此,ΔABC的极三角形的三内角分别是
.
定理3.4 若ΔABC的球面极三角形是ΔA*B*C*,则ΔA*B*C*的球面极三角形是ΔABC.因此球面极三角形总是成对出现的.由例1、例2可得 设ΔABC的三边长为a,b,c,三内角为A,B,C;
ΔA*B*C*的三边长为a*,b*,c*,三内角为A*,B*,C*.我们把a,A*;A,a*等叫做ΔABC与它的极三角形ΔA*B*C*的一对对应元素.定理3.5 在单位球面上,ΔABC与它的极三角形
ΔA*B*C*的对应元素满足
a*=π-A,b*=π-B,c*=π-C;
a=π-A*, b=π-B*, c=π-C*.问题解决: 设ΔA*B*C*是ΔABC的极三角形,则
A=π-a*,B=π-b*,C=π-c*,
A+B+C=3π-(a*+b*+c*)<3π.
因此,对于球面ΔABC的三内角A,B,C,满足
π
3.球面极三角形对应元素的关系;
4.球面三角形内角和.课堂小结作业布置P26习题3.3 4,7谢谢指导!
同课章节目录
