三角形的内角(含习题及答案)
文档属性
| 名称 | 三角形的内角(含习题及答案) |  | |
| 格式 | rar | ||
| 文件大小 | 189.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-10 22:01:00 | ||
图片预览

文档简介
登陆21世纪教育 助您教考全无忧
三角形的内角
教学目标
1.经历实验活动的过程,得出三角形的内角和定理,能用平行线的性质推出这一定理.
2.能应用三角形内角和定理解决一些简单的实际问题.
重点:三角形内角和定理
难点:三角形内角和定理的推理的过程
课前准备
每个学生准备好二个由硬纸片剪出的三角形
教学过程
一、做一做
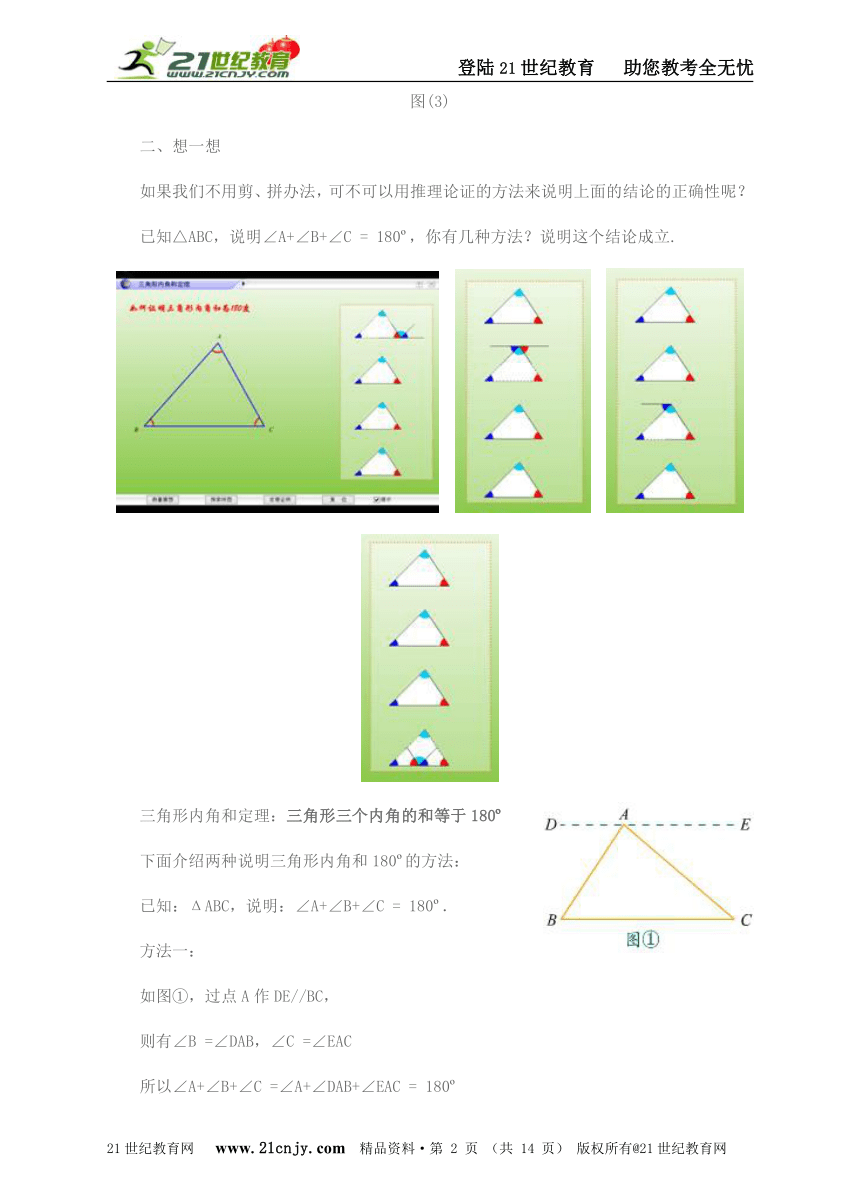
1)在所准备的三角形硬纸片上标出三个内角的编码.
2)让学生动手把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出∠BCD的度数,可得到∠A+∠B+∠ACB = 180 .
3)把∠B和∠C剪下按图(3)拼在一起,用量角器量一量∠MAN的度数,会得到什么结果?
图(3)
二、想一想
如果我们不用剪、拼办法,可不可以用推理论证的方法来说明上面的结论的正确性呢?
已知△ABC,说明∠A+∠B+∠C = 180 ,你有几种方法?说明这个结论成立.
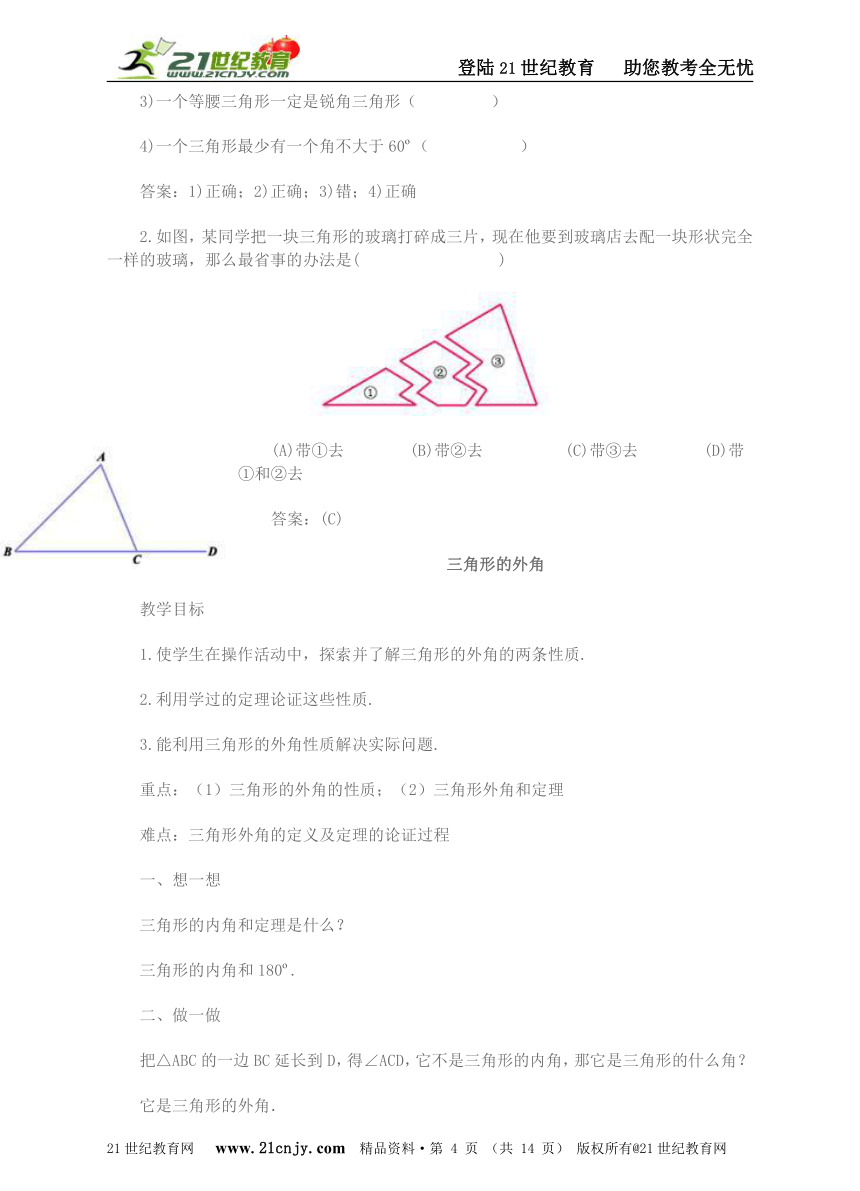
三角形内角和定理:三角形三个内角的和等于180
下面介绍两种说明三角形内角和180 的方法:
已知:ΔABC,说明:∠A+∠B+∠C = 180 .
方法一:
如图①,过点A作DE//BC,
则有∠B =∠DAB,∠C =∠EAC
所以∠A+∠B+∠C =∠A+∠DAB+∠EAC = 180
方法二:
如图②,延长BC,过点C作CD//AB,
则有∠A =∠ACD,∠B =∠DCE
所以∠A+∠B+∠C =∠ACD+∠DCE+∠C = 180
推论:直角三角形的两个锐角互余.
三、例题如图,C岛在A岛的北偏东50 方向,B岛在A岛的北偏东80 方向,C岛在B岛的北偏西40 方向,从C岛看A、B两岛的视角∠ACB是多少度?
分析:A、B、C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个内角;如果能求出∠CAB、∠ABC,就能求出∠ACB
解:∠CAB =∠BAD ∠CAD = 80 50 = 30
由AD//BE,可得∠BAD+∠ABE = 180
所以∠ABE及= 180 ∠BAD = 180 80 = 100 ,∠ABC =∠ABE ∠EBC = 100 40 = 60
在△ABC中,∠ACB = 180 ∠ACB ∠CAB = 180 60 30 = 90
答:从C岛看A、B两岛的视角∠ACB是90 .
补充练习:
1.判断题:
1)三角形中最大的角是70 ,那么这个三角形是锐角三角形( )
2)一个三角形中最多只有一个钝角或直角( )
3)一个等腰三角形一定是锐角三角形( )
4)一个三角形最少有一个角不大于60 ( )
答案:1)正确;2)正确;3)错;4)正确
2.如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是( )
(A)带①去 (B)带②去 (C)带③去 (D)带①和②去
答案:(C)
三角形的外角
教学目标
1.使学生在操作活动中,探索并了解三角形的外角的两条性质.
2.利用学过的定理论证这些性质.
3.能利用三角形的外角性质解决实际问题.
重点:(1)三角形的外角的性质;(2)三角形外角和定理
难点:三角形外角的定义及定理的论证过程
一、想一想
三角形的内角和定理是什么?
三角形的内角和180 .
二、做一做
把△ABC的一边BC延长到D,得∠ACD,它不是三角形的内角,那它是三角形的什么角?
它是三角形的外角.
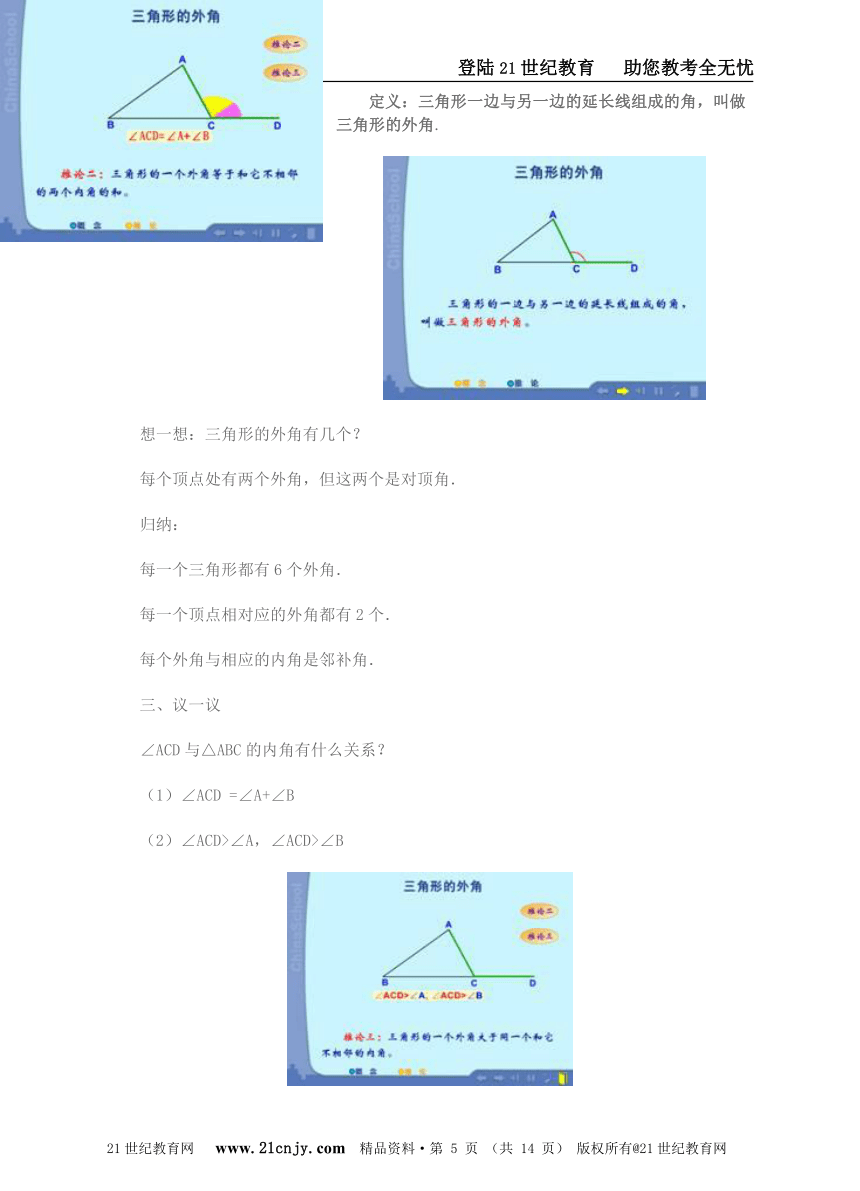
定义:三角形一边与另一边的延长线组成的角,叫做三角形的外角.
想一想:三角形的外角有几个?
每个顶点处有两个外角,但这两个是对顶角.
归纳:
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个.
每个外角与相应的内角是邻补角.
三、议一议
∠ACD与△ABC的内角有什么关系?
(1)∠ACD =∠A+∠B
(2)∠ACD>∠A,∠ACD>∠B
再画△ABC的外角试一试,还会得到这个性质吗?
同学用几何语言叙述这个性质:
三角形的一个外角等于它不相邻的两个内角之和;
三角形的一个外角大于与它不相邻的任何一个内角.
你能用学过的定理说明这些定理的成立吗?
已知:∠ACD是△ABC的外角
说明:
(1)∠ACD =∠A+∠B
(2)∠ACD>∠A,∠ACD>∠B
结合图形给予说明
说明:因为∠ACD是△ABC的外角,根据外角的定义,知∠ACD+∠ACB = 180
又根据三角形内角和定理知∠A+∠B+∠ACB = 180
所以∠ACD =∠A+∠B
显然∠ACD =∠A+∠B>∠A,同时∠ACD =∠A+∠B>∠B
三角形的外角与内角的关系:
1.三角形的一个外角与它相邻的内角互补;
2.三角形的一个外角等于与它不相邻的两个内角的和;
3.三角形的一个外角大于任何一个与它不相邻的内角.
备选题
1)如图,∠1,∠2,∠3是△ABC的不同三个外角,则∠1+∠2+∠3 =
2)三角形的三个外角中最多有 锐角,最多有 个钝角,最多有 个直角
3)△ABC的两个内角的一平分线交于点E,∠A = 52 ,则∠BEC =
4)已知△ABC的∠B,∠C的外角平分线交于点D,∠A = 40 ,那么∠D =
5)在△ABC中∠A等于和它相邻的外角的四分之一,这个外角等于∠B的两倍,那么
∠A = ,∠B = ,∠C =
答案:1)360 ;2)一个、三个、一个;3)116 ;4)70 ;5)36 、72 、72
典型例题
例题:
1.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180
B.240
C.360
D.540
答案:C
说明:因为三角形内角和为180 ,所以∠A+∠C+∠E = 180 ,∠B+∠D+∠F = 180 ,所以∠A+∠B+∠C+∠D+∠E+∠F的度数为360 .
2.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180
B.360
C.540
D.240
答案:B
说明:由三角形内角和为180 ,知∠A+∠B+∠APB = 180 ,∠C+∠D+∠CQD = 180 ,∠E+∠F+∠ERF = 180 ,∠RPQ+∠PQR+∠QRP = 180 ,因为∠APB =∠RPQ,∠CQD =∠PQR,∠ERF =∠QRP,所以∠APB+∠CQD+∠ERF = 180 ;而∠A+∠B+∠C+∠D+∠E+∠F = 180 ∠APB+180 ∠CQD+180 ∠ERF = 540 (∠APB+∠CQD+∠ERF) = 540 180 = 360 ,所以答案为B.
3.一个三角形的三个内角之比为2:3:4,那么这个三角形的最大内角的度数为________.
答案:80
说明:由已知可设这个三角形的三个内角度数为2x,3x,4x,则有2x+3x+4x = 180 ,所以x = 20 ,这样这个三角形的三个内角的度数分别是40 ,60 和80 ,所以这个三角形的最大内角为80 .
4.在△ABC中,∠A = 50 ,点P是∠B、∠C平分线的交点,则∠BPC的度数是( )
A.65
B.115
C.130
D.100
答案:B
说明:不难得到∠ABC+∠ACB = 180 50 = 130 ,BP为∠ABC的平分线,CP为∠ACB的平分线,即∠ABC = 2∠PBC,∠ACB = 2∠PCB,所以∠PBC+∠PCB = (∠ABC+∠ACB)÷2 = 130 ÷2 = 65 ,因此,在ΔBPC中,可求得∠BPC = 180 (∠PBC+∠PCB) = 180 65 = 115 ,所以答案为B.
5.在△ABC中,若∠A =∠B =∠C,求∠C的度数?
答案:∠C = 90
说明:设∠A的度数为x,则根据已知不难得到∠B的度数是2x,∠C的度数是3x;由三角形内角和为180 ,有x+2x+3x = 180 ,解得x = 30 ,这时3x = 90 ,即∠C的度数为90 .
习题一
一、选择题:
1.如果三角形的三个内角的度数比是2:3:4,则它是( )毛
A.锐角三角形 B.钝角三角形 C.直角三角形 D.钝角或直角三角形
2.下列说法正确的是( )
A.三角形的内角中最多有一个锐角 B.三角形的内角中最多有两个锐角
C.三角形的内角中最多有一个直角 D.三角形的内角都大于60°
3.已知三角形的一个内角是另一个内角的,是第三个内角的,则这个三角形各内角的度数分别为( )
A.60°,90°,75° B.48°,72°,60°
C.48°,32°,38° D.40°,50°,90°
4.已知△ABC中,∠A=2(∠B+∠C),则∠A的度数为( )
A.100° B.120° C.140° D.160°
5.已知三角形两个内角的差等于第三个内角,则它是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等边三角形
6.设α,β,γ是某三角形的三个内角,则α+β,β+γ,α+γ 中 ( )
A.有两个锐角、一个钝角 B.有两个钝角、一个锐角
C.至少有两个钝角 D.三个都可能是锐角
7.在△ABC中,∠A=∠B=∠C,则此三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
二、填空题:
1.三角形中,若最大内角等于最小内角的2倍,最大内角又比另一个内角大20 ,则此三角形的最小内角的度数是________.
2.在△ABC中,若∠A+∠B=∠C,则此三角形为_______三角形;若∠A+∠B<∠C,则此三角形是_____三角形.
3.已知等腰三角形的两个内角的度数之比为1:2,则这个等腰三角形的顶角为_______.
4.在△ABC中,∠B,∠C的平分线交于点O,若∠BOC=132 ,则∠A=_______度.
5.如图,已知∠1=20 ,∠2=25 ,∠A=35 ,则∠BDC的度数为________.
三、基础训练:
1.如图,在△ABC中,AD⊥BC于D,AE平分∠BAC(∠C>∠B),
试说明∠EAD=(∠C ∠B).
2.在△ABC中,已知∠B ∠A=5°,∠C ∠B=20°,求三角形各内角的度数.
四、提高训练:
如图所示,已知∠1=∠2,∠3=∠4,∠C=32 ,∠D=28 ,求∠P的度数.
五、探索发现:
如图,将△ABC沿EF折叠,使点C落到点C′处,试探求∠1,∠2与∠C的关系.
六、中考题与竞赛题:
(2001·天津)如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,
∠AFD=158°, 则∠EDF=________度.
答案:
一、1.A 2.C 3.B 4.B 5.C 6.C 7.B
二、1.40° 2.直角 钝角 3.36°或90° 4.84 5.80°
三、1.解:∵AD⊥BC,
∴∠BDA=90 ,
∴∠BAD=90 ∠B,
又∵AE 平分∠BAC,
∴∠BAE=∠BAC=(180 ∠B ∠C),
∴∠EAD=∠BAD ∠BAE
=90 ∠B (180 ∠B ∠C)
=90 ∠B 90 +∠B+∠C
=∠C ∠B
=(∠C ∠B).
2.∠A=50 ,∠B=55 ,∠C=75 .
四、∠P=30°
五、解:∵∠1=180 2∠CEF,∠2=180 2∠CFE,
∴∠1+∠2=360 2(∠CEF+∠CFE)
=360 2(180 ∠C)
=360 360 +2∠C=2∠C.
六、68.毛
习题二
一、选择题:
1.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )毛
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确定
2.如果三角形的一个外角和与它不相邻的两个内角的和为180 ,那么与这个外角相邻的内角的度数为( )
A.30° B.60° C.90° D.120°
3.已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为( )
A.90° B.110° C.100° D.120°
4.已知等腰三角形的一个外角是120 ,则它是( )
A.等腰直角三角形 B.一般的等腰三角形 C.等边三角形 D.等腰钝角三角形
5.如图(1)所示,若∠A=32 ,∠B=45 ,∠C=38 ,则∠DFE等于( )
A.120° B.115° C.110° D.105°
(1) (2) (3)
6.如图(2)所示,在△ABC中,E,F分别在AB,AC上,则下列各式不能成立的是( )
A.∠BOC=∠2+∠6+∠A B.∠2=∠5 ∠A C.∠5=∠1+∠4 D.∠1=∠ABC+∠4
二、填空题:
1.三角形的三个外角中,最多有_______个锐角.
2.如图(3)所示,∠1=_______.
3.如果一个三角形的各内角与一个外角的和是225 ,则与这个外角相邻的内角是____度.
4.已知等腰三角形的一个外角为150 ,则它的底角为_____.
5.如图,∠ABC,∠ACB的内角平分线交于点O,∠ABC 的内角平分线与∠ACB的外角平分线交于点D,∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60 , 则∠BOC=_______,∠D=_____,∠E=________.
6.如图,∠A=50 ,∠B=40 ,∠C=30 ,则∠BDC=________.
三、基础训练:
如图,在△ABC中,∠A=70 ,BO,CO分别平分∠ABC和∠ACB,求∠BOC的度数.
四、提高训练:
如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63 , 求∠DAC的度数.
五、探索发现:
如图,在△ABC中,∠A=α,△ABC的内角平分线或外角平分线交于点P,且∠P=β,试探求下列各图中α与β的关系,并选择一个加以说明.
六、中考题与竞赛题:
(2004·吉林)如图所示,∠CAB的外角等于120 ,∠B等于40 ,则∠C 的度数是_______.
答案:
一、1.C 2.C 3.C 4.C 5.B 6.C
二、1.1 2.120° 3.95 4.30°或75° 5.120° 30° 60° 6.120°
三、∠BOC=125°
四、∠DAC=24°
五、(1)β = 90 +α;(2)β =α;(3)β = 90 α (说明略)
六、80 .毛
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 13 页) 版权所有@21世纪教育网
三角形的内角
教学目标
1.经历实验活动的过程,得出三角形的内角和定理,能用平行线的性质推出这一定理.
2.能应用三角形内角和定理解决一些简单的实际问题.
重点:三角形内角和定理
难点:三角形内角和定理的推理的过程
课前准备
每个学生准备好二个由硬纸片剪出的三角形
教学过程
一、做一做
1)在所准备的三角形硬纸片上标出三个内角的编码.
2)让学生动手把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出∠BCD的度数,可得到∠A+∠B+∠ACB = 180 .
3)把∠B和∠C剪下按图(3)拼在一起,用量角器量一量∠MAN的度数,会得到什么结果?
图(3)
二、想一想
如果我们不用剪、拼办法,可不可以用推理论证的方法来说明上面的结论的正确性呢?
已知△ABC,说明∠A+∠B+∠C = 180 ,你有几种方法?说明这个结论成立.
三角形内角和定理:三角形三个内角的和等于180
下面介绍两种说明三角形内角和180 的方法:
已知:ΔABC,说明:∠A+∠B+∠C = 180 .
方法一:
如图①,过点A作DE//BC,
则有∠B =∠DAB,∠C =∠EAC
所以∠A+∠B+∠C =∠A+∠DAB+∠EAC = 180
方法二:
如图②,延长BC,过点C作CD//AB,
则有∠A =∠ACD,∠B =∠DCE
所以∠A+∠B+∠C =∠ACD+∠DCE+∠C = 180
推论:直角三角形的两个锐角互余.
三、例题如图,C岛在A岛的北偏东50 方向,B岛在A岛的北偏东80 方向,C岛在B岛的北偏西40 方向,从C岛看A、B两岛的视角∠ACB是多少度?
分析:A、B、C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个内角;如果能求出∠CAB、∠ABC,就能求出∠ACB
解:∠CAB =∠BAD ∠CAD = 80 50 = 30
由AD//BE,可得∠BAD+∠ABE = 180
所以∠ABE及= 180 ∠BAD = 180 80 = 100 ,∠ABC =∠ABE ∠EBC = 100 40 = 60
在△ABC中,∠ACB = 180 ∠ACB ∠CAB = 180 60 30 = 90
答:从C岛看A、B两岛的视角∠ACB是90 .
补充练习:
1.判断题:
1)三角形中最大的角是70 ,那么这个三角形是锐角三角形( )
2)一个三角形中最多只有一个钝角或直角( )
3)一个等腰三角形一定是锐角三角形( )
4)一个三角形最少有一个角不大于60 ( )
答案:1)正确;2)正确;3)错;4)正确
2.如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是( )
(A)带①去 (B)带②去 (C)带③去 (D)带①和②去
答案:(C)
三角形的外角
教学目标
1.使学生在操作活动中,探索并了解三角形的外角的两条性质.
2.利用学过的定理论证这些性质.
3.能利用三角形的外角性质解决实际问题.
重点:(1)三角形的外角的性质;(2)三角形外角和定理
难点:三角形外角的定义及定理的论证过程
一、想一想
三角形的内角和定理是什么?
三角形的内角和180 .
二、做一做
把△ABC的一边BC延长到D,得∠ACD,它不是三角形的内角,那它是三角形的什么角?
它是三角形的外角.
定义:三角形一边与另一边的延长线组成的角,叫做三角形的外角.
想一想:三角形的外角有几个?
每个顶点处有两个外角,但这两个是对顶角.
归纳:
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个.
每个外角与相应的内角是邻补角.
三、议一议
∠ACD与△ABC的内角有什么关系?
(1)∠ACD =∠A+∠B
(2)∠ACD>∠A,∠ACD>∠B
再画△ABC的外角试一试,还会得到这个性质吗?
同学用几何语言叙述这个性质:
三角形的一个外角等于它不相邻的两个内角之和;
三角形的一个外角大于与它不相邻的任何一个内角.
你能用学过的定理说明这些定理的成立吗?
已知:∠ACD是△ABC的外角
说明:
(1)∠ACD =∠A+∠B
(2)∠ACD>∠A,∠ACD>∠B
结合图形给予说明
说明:因为∠ACD是△ABC的外角,根据外角的定义,知∠ACD+∠ACB = 180
又根据三角形内角和定理知∠A+∠B+∠ACB = 180
所以∠ACD =∠A+∠B
显然∠ACD =∠A+∠B>∠A,同时∠ACD =∠A+∠B>∠B
三角形的外角与内角的关系:
1.三角形的一个外角与它相邻的内角互补;
2.三角形的一个外角等于与它不相邻的两个内角的和;
3.三角形的一个外角大于任何一个与它不相邻的内角.
备选题
1)如图,∠1,∠2,∠3是△ABC的不同三个外角,则∠1+∠2+∠3 =
2)三角形的三个外角中最多有 锐角,最多有 个钝角,最多有 个直角
3)△ABC的两个内角的一平分线交于点E,∠A = 52 ,则∠BEC =
4)已知△ABC的∠B,∠C的外角平分线交于点D,∠A = 40 ,那么∠D =
5)在△ABC中∠A等于和它相邻的外角的四分之一,这个外角等于∠B的两倍,那么
∠A = ,∠B = ,∠C =
答案:1)360 ;2)一个、三个、一个;3)116 ;4)70 ;5)36 、72 、72
典型例题
例题:
1.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180
B.240
C.360
D.540
答案:C
说明:因为三角形内角和为180 ,所以∠A+∠C+∠E = 180 ,∠B+∠D+∠F = 180 ,所以∠A+∠B+∠C+∠D+∠E+∠F的度数为360 .
2.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180
B.360
C.540
D.240
答案:B
说明:由三角形内角和为180 ,知∠A+∠B+∠APB = 180 ,∠C+∠D+∠CQD = 180 ,∠E+∠F+∠ERF = 180 ,∠RPQ+∠PQR+∠QRP = 180 ,因为∠APB =∠RPQ,∠CQD =∠PQR,∠ERF =∠QRP,所以∠APB+∠CQD+∠ERF = 180 ;而∠A+∠B+∠C+∠D+∠E+∠F = 180 ∠APB+180 ∠CQD+180 ∠ERF = 540 (∠APB+∠CQD+∠ERF) = 540 180 = 360 ,所以答案为B.
3.一个三角形的三个内角之比为2:3:4,那么这个三角形的最大内角的度数为________.
答案:80
说明:由已知可设这个三角形的三个内角度数为2x,3x,4x,则有2x+3x+4x = 180 ,所以x = 20 ,这样这个三角形的三个内角的度数分别是40 ,60 和80 ,所以这个三角形的最大内角为80 .
4.在△ABC中,∠A = 50 ,点P是∠B、∠C平分线的交点,则∠BPC的度数是( )
A.65
B.115
C.130
D.100
答案:B
说明:不难得到∠ABC+∠ACB = 180 50 = 130 ,BP为∠ABC的平分线,CP为∠ACB的平分线,即∠ABC = 2∠PBC,∠ACB = 2∠PCB,所以∠PBC+∠PCB = (∠ABC+∠ACB)÷2 = 130 ÷2 = 65 ,因此,在ΔBPC中,可求得∠BPC = 180 (∠PBC+∠PCB) = 180 65 = 115 ,所以答案为B.
5.在△ABC中,若∠A =∠B =∠C,求∠C的度数?
答案:∠C = 90
说明:设∠A的度数为x,则根据已知不难得到∠B的度数是2x,∠C的度数是3x;由三角形内角和为180 ,有x+2x+3x = 180 ,解得x = 30 ,这时3x = 90 ,即∠C的度数为90 .
习题一
一、选择题:
1.如果三角形的三个内角的度数比是2:3:4,则它是( )毛
A.锐角三角形 B.钝角三角形 C.直角三角形 D.钝角或直角三角形
2.下列说法正确的是( )
A.三角形的内角中最多有一个锐角 B.三角形的内角中最多有两个锐角
C.三角形的内角中最多有一个直角 D.三角形的内角都大于60°
3.已知三角形的一个内角是另一个内角的,是第三个内角的,则这个三角形各内角的度数分别为( )
A.60°,90°,75° B.48°,72°,60°
C.48°,32°,38° D.40°,50°,90°
4.已知△ABC中,∠A=2(∠B+∠C),则∠A的度数为( )
A.100° B.120° C.140° D.160°
5.已知三角形两个内角的差等于第三个内角,则它是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等边三角形
6.设α,β,γ是某三角形的三个内角,则α+β,β+γ,α+γ 中 ( )
A.有两个锐角、一个钝角 B.有两个钝角、一个锐角
C.至少有两个钝角 D.三个都可能是锐角
7.在△ABC中,∠A=∠B=∠C,则此三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
二、填空题:
1.三角形中,若最大内角等于最小内角的2倍,最大内角又比另一个内角大20 ,则此三角形的最小内角的度数是________.
2.在△ABC中,若∠A+∠B=∠C,则此三角形为_______三角形;若∠A+∠B<∠C,则此三角形是_____三角形.
3.已知等腰三角形的两个内角的度数之比为1:2,则这个等腰三角形的顶角为_______.
4.在△ABC中,∠B,∠C的平分线交于点O,若∠BOC=132 ,则∠A=_______度.
5.如图,已知∠1=20 ,∠2=25 ,∠A=35 ,则∠BDC的度数为________.
三、基础训练:
1.如图,在△ABC中,AD⊥BC于D,AE平分∠BAC(∠C>∠B),
试说明∠EAD=(∠C ∠B).
2.在△ABC中,已知∠B ∠A=5°,∠C ∠B=20°,求三角形各内角的度数.
四、提高训练:
如图所示,已知∠1=∠2,∠3=∠4,∠C=32 ,∠D=28 ,求∠P的度数.
五、探索发现:
如图,将△ABC沿EF折叠,使点C落到点C′处,试探求∠1,∠2与∠C的关系.
六、中考题与竞赛题:
(2001·天津)如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,
∠AFD=158°, 则∠EDF=________度.
答案:
一、1.A 2.C 3.B 4.B 5.C 6.C 7.B
二、1.40° 2.直角 钝角 3.36°或90° 4.84 5.80°
三、1.解:∵AD⊥BC,
∴∠BDA=90 ,
∴∠BAD=90 ∠B,
又∵AE 平分∠BAC,
∴∠BAE=∠BAC=(180 ∠B ∠C),
∴∠EAD=∠BAD ∠BAE
=90 ∠B (180 ∠B ∠C)
=90 ∠B 90 +∠B+∠C
=∠C ∠B
=(∠C ∠B).
2.∠A=50 ,∠B=55 ,∠C=75 .
四、∠P=30°
五、解:∵∠1=180 2∠CEF,∠2=180 2∠CFE,
∴∠1+∠2=360 2(∠CEF+∠CFE)
=360 2(180 ∠C)
=360 360 +2∠C=2∠C.
六、68.毛
习题二
一、选择题:
1.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )毛
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确定
2.如果三角形的一个外角和与它不相邻的两个内角的和为180 ,那么与这个外角相邻的内角的度数为( )
A.30° B.60° C.90° D.120°
3.已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为( )
A.90° B.110° C.100° D.120°
4.已知等腰三角形的一个外角是120 ,则它是( )
A.等腰直角三角形 B.一般的等腰三角形 C.等边三角形 D.等腰钝角三角形
5.如图(1)所示,若∠A=32 ,∠B=45 ,∠C=38 ,则∠DFE等于( )
A.120° B.115° C.110° D.105°
(1) (2) (3)
6.如图(2)所示,在△ABC中,E,F分别在AB,AC上,则下列各式不能成立的是( )
A.∠BOC=∠2+∠6+∠A B.∠2=∠5 ∠A C.∠5=∠1+∠4 D.∠1=∠ABC+∠4
二、填空题:
1.三角形的三个外角中,最多有_______个锐角.
2.如图(3)所示,∠1=_______.
3.如果一个三角形的各内角与一个外角的和是225 ,则与这个外角相邻的内角是____度.
4.已知等腰三角形的一个外角为150 ,则它的底角为_____.
5.如图,∠ABC,∠ACB的内角平分线交于点O,∠ABC 的内角平分线与∠ACB的外角平分线交于点D,∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60 , 则∠BOC=_______,∠D=_____,∠E=________.
6.如图,∠A=50 ,∠B=40 ,∠C=30 ,则∠BDC=________.
三、基础训练:
如图,在△ABC中,∠A=70 ,BO,CO分别平分∠ABC和∠ACB,求∠BOC的度数.
四、提高训练:
如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63 , 求∠DAC的度数.
五、探索发现:
如图,在△ABC中,∠A=α,△ABC的内角平分线或外角平分线交于点P,且∠P=β,试探求下列各图中α与β的关系,并选择一个加以说明.
六、中考题与竞赛题:
(2004·吉林)如图所示,∠CAB的外角等于120 ,∠B等于40 ,则∠C 的度数是_______.
答案:
一、1.C 2.C 3.C 4.C 5.B 6.C
二、1.1 2.120° 3.95 4.30°或75° 5.120° 30° 60° 6.120°
三、∠BOC=125°
四、∠DAC=24°
五、(1)β = 90 +α;(2)β =α;(3)β = 90 α (说明略)
六、80 .毛
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 13 页) 版权所有@21世纪教育网
