苏教版高中数学选修3-4 点的轴对称变换
文档属性
| 名称 | 苏教版高中数学选修3-4 点的轴对称变换 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 00:00:00 | ||
图片预览





文档简介
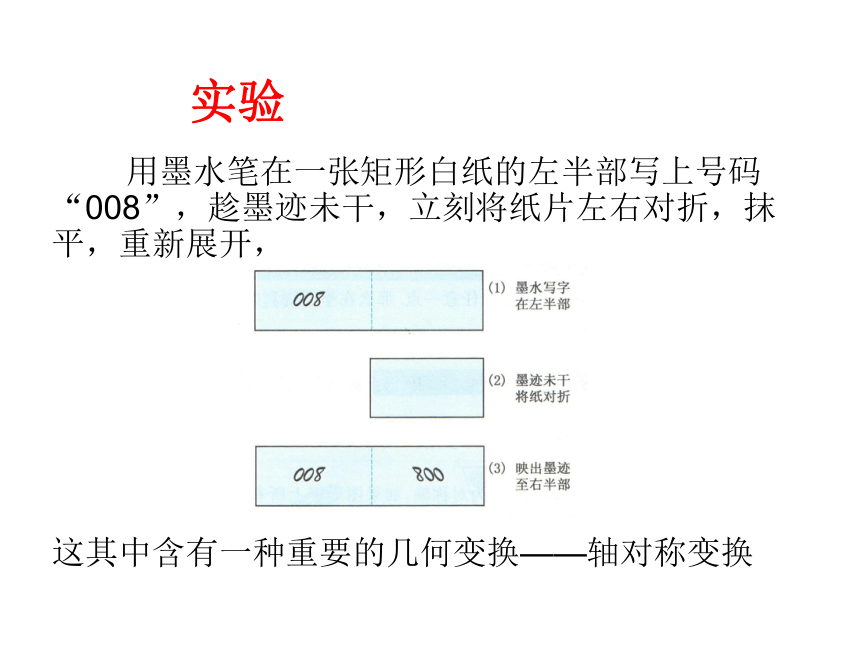
课件17张PPT。点的轴对称变换实验 用墨水笔在一张矩形白纸的左半部写上号码“008”,趁墨迹未干,立刻将纸片左右对折,抹平,重新展开,
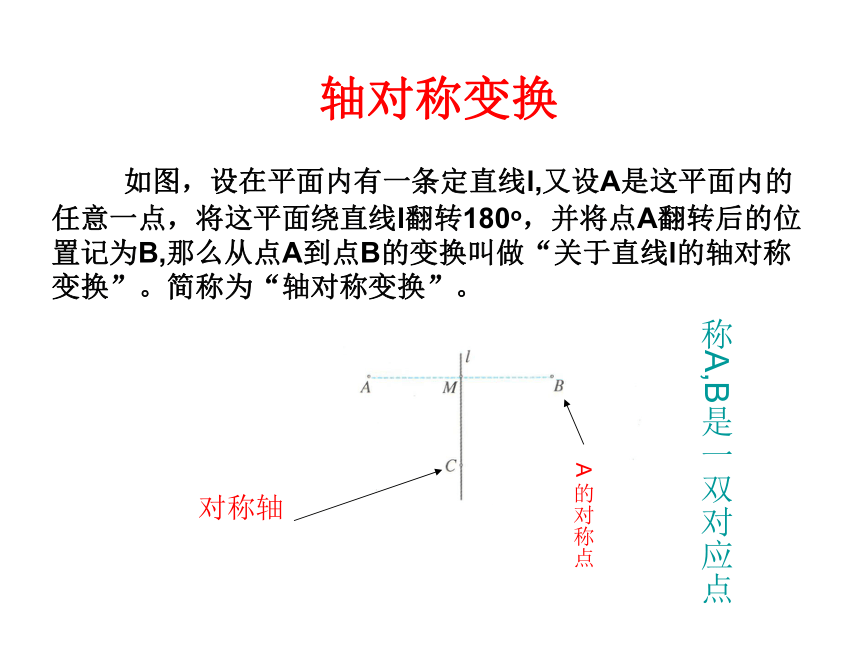
这其中含有一种重要的几何变换——轴对称变换轴对称变换 如图,设在平面内有一条定直线l,又设A是这平面内的任意一点,将这平面绕直线l翻转180o,并将点A翻转后的位置记为B,那么从点A到点B的变换叫做“关于直线l的轴对称变换”。简称为“轴对称变换”。对称轴
A 的对称点称A,B是一双对应点 如果点A不在对称轴上,B是A的对称点,那么A,B分居直线l的两侧,并且AB⊥l;又若AB与l的交点为M,则AM=MB(如上图)。
以上性质可简述为:
在轴对称变换下,任意一双对应点的连线被对称轴垂直平分。轴对称性质 设C是对称轴l上的任意一点,那么在平面绕直线l翻转180以后,点C保持不动。
由此可见:
在轴对称变换下,对称轴上的任意点变成它自己。
剪纸欣赏轴对称作用1.可以通过对称轴的一边从而画出另
一边.?
2.可以通过画对称轴得出的两个图形
全等.?
3.扩展到轴对称的应用以及函数图像
的意义.轴对称应用 传说亚历山大城有一位精通数学和物理 学者,名叫海伦。一天,一位罗马将军专程去拜访他,向他请教一个百思不得解的问题:
军官每天从军营A出发先到河边P处饮马,然后再去河岸同侧的B地去开会,应该怎样走才能使路程最短?1、经典问题:将军饮马1、作点A关于直线的对称点C.
2、此时点C与点B的最短距离是CB.
3、此时点P就是将军饮马的位置.证明:如图,在l上任取一点P1,连结P1A,
P1B,P1C,
因为P1A+P1B=P1C+P1B>BC=PA+PB.
这是根据三角形两边之和大于第三边,所以结论成立.问题本质:
实际上就是“折化直”问题,利用两点之间线段最短.从数学思想的角度来看,实际体现了转化思想,通过什么方法来实现转化思想——轴对称变换.2、在解题中应用 例1 已知点A的坐标为(2x+y-3,x-2y),它关于x轴对称的点A'的坐标为(x+3,y-4),则点A关于y轴对称点的坐标为__________.
解:因为点关于x轴对称的坐标特点是:横坐标相等,纵坐标相反.所以2x+y-3=x+3,x-2y+y-4=0,
解得x=5,y=1,即点A(8,3).
关于y轴对称的点的特征是:横坐标相反,纵坐标相等,因此所求点的坐标是(-8,3). 例2 在如图中,若A到直线L的距离AC是3千米,B到直线L的距离BD是1千米,并且CD的距离4千米,在直线L上找一点P,使PA+PB的值最小,求这个最小值.
解:如图,只要过A1点画直线L的平行线与BD的延长线交于H,在RtΔA1BH中,A1H=4千米,BH=4千米,用勾股定理求得A1B的长度为 千米.即PA+PB的最小值为 千米. 例3 求函数 的最小值.
解:方法(1),把原函数转化为 ,因此可以理解为在x轴上找一个点,使它到点(3,1)和(-3,5)的距离之和最小.
方法(2),如图,分别以PM=3-x,AM=1为边和以PN=x+3,BN=5为边构建使3-x和x+3在同一直线上的两个直角ΔPAM,ΔPBN,两条斜边的长就是PA=
和PB= ,因此,求Y的最小值就
是求PA+PB的最小值,只要利用轴对称性质求出
BA的长,就是Y的最小值.( )1.轴对称变换的定义;
2.轴对称变换的性质;
3.轴对称变换的应用.谢谢指导!
这其中含有一种重要的几何变换——轴对称变换轴对称变换 如图,设在平面内有一条定直线l,又设A是这平面内的任意一点,将这平面绕直线l翻转180o,并将点A翻转后的位置记为B,那么从点A到点B的变换叫做“关于直线l的轴对称变换”。简称为“轴对称变换”。对称轴
A 的对称点称A,B是一双对应点 如果点A不在对称轴上,B是A的对称点,那么A,B分居直线l的两侧,并且AB⊥l;又若AB与l的交点为M,则AM=MB(如上图)。
以上性质可简述为:
在轴对称变换下,任意一双对应点的连线被对称轴垂直平分。轴对称性质 设C是对称轴l上的任意一点,那么在平面绕直线l翻转180以后,点C保持不动。
由此可见:
在轴对称变换下,对称轴上的任意点变成它自己。
剪纸欣赏轴对称作用1.可以通过对称轴的一边从而画出另
一边.?
2.可以通过画对称轴得出的两个图形
全等.?
3.扩展到轴对称的应用以及函数图像
的意义.轴对称应用 传说亚历山大城有一位精通数学和物理 学者,名叫海伦。一天,一位罗马将军专程去拜访他,向他请教一个百思不得解的问题:
军官每天从军营A出发先到河边P处饮马,然后再去河岸同侧的B地去开会,应该怎样走才能使路程最短?1、经典问题:将军饮马1、作点A关于直线的对称点C.
2、此时点C与点B的最短距离是CB.
3、此时点P就是将军饮马的位置.证明:如图,在l上任取一点P1,连结P1A,
P1B,P1C,
因为P1A+P1B=P1C+P1B>BC=PA+PB.
这是根据三角形两边之和大于第三边,所以结论成立.问题本质:
实际上就是“折化直”问题,利用两点之间线段最短.从数学思想的角度来看,实际体现了转化思想,通过什么方法来实现转化思想——轴对称变换.2、在解题中应用 例1 已知点A的坐标为(2x+y-3,x-2y),它关于x轴对称的点A'的坐标为(x+3,y-4),则点A关于y轴对称点的坐标为__________.
解:因为点关于x轴对称的坐标特点是:横坐标相等,纵坐标相反.所以2x+y-3=x+3,x-2y+y-4=0,
解得x=5,y=1,即点A(8,3).
关于y轴对称的点的特征是:横坐标相反,纵坐标相等,因此所求点的坐标是(-8,3). 例2 在如图中,若A到直线L的距离AC是3千米,B到直线L的距离BD是1千米,并且CD的距离4千米,在直线L上找一点P,使PA+PB的值最小,求这个最小值.
解:如图,只要过A1点画直线L的平行线与BD的延长线交于H,在RtΔA1BH中,A1H=4千米,BH=4千米,用勾股定理求得A1B的长度为 千米.即PA+PB的最小值为 千米. 例3 求函数 的最小值.
解:方法(1),把原函数转化为 ,因此可以理解为在x轴上找一个点,使它到点(3,1)和(-3,5)的距离之和最小.
方法(2),如图,分别以PM=3-x,AM=1为边和以PN=x+3,BN=5为边构建使3-x和x+3在同一直线上的两个直角ΔPAM,ΔPBN,两条斜边的长就是PA=
和PB= ,因此,求Y的最小值就
是求PA+PB的最小值,只要利用轴对称性质求出
BA的长,就是Y的最小值.( )1.轴对称变换的定义;
2.轴对称变换的性质;
3.轴对称变换的应用.谢谢指导!
同课章节目录
