苏教版高中数学选修3-4 4.2.2中心对称图形.
文档属性
| 名称 | 苏教版高中数学选修3-4 4.2.2中心对称图形. |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 00:00:00 | ||
图片预览




文档简介
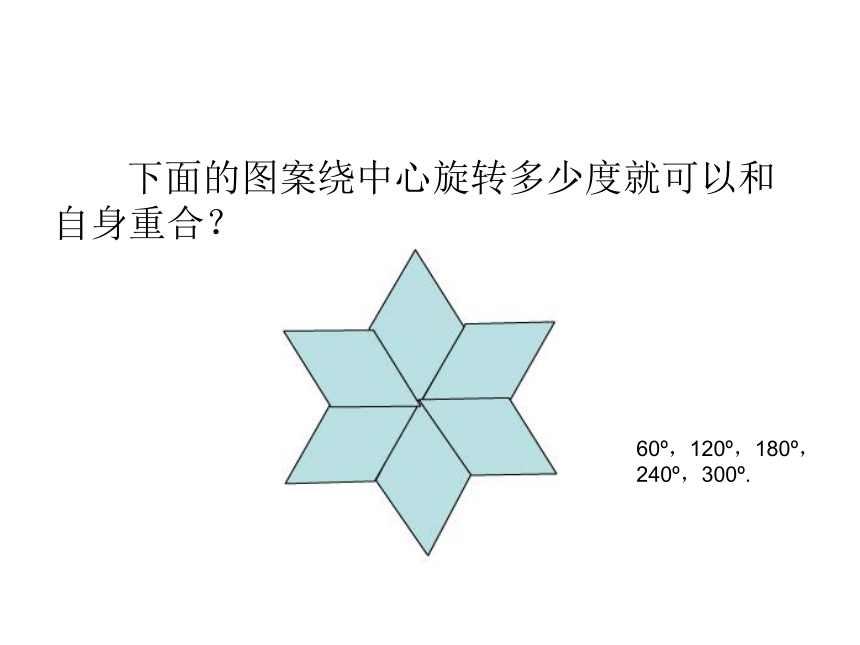
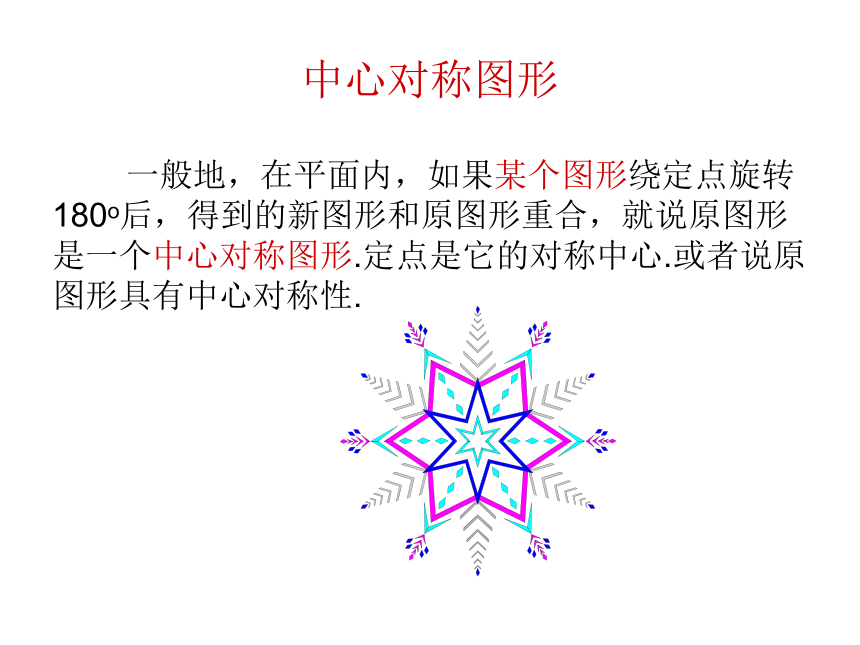
课件14张PPT。§4.2.2 中心对称图形图片欣赏 下面的图案绕中心旋转多少度就可以和自身重合?60o,120o,180o,240o,300o. 设线段AB的中点为O,将这条线段绕点O旋转180o,结果端点A转到B的位置,端点B转到A的位置,整条线段依旧落在A与B之间,与原线段完全重合,图形外貌未改,只不过转了一个身,线段内部各点左右成对地交换场地. 如图,设平行四边形ABCD的对角线交点为O,将它绕点O旋转180o,结果与原平行四边形重合.平行四边形外貌依旧,只不过它的边AB与CD交换了位置,BC与DA交换了位置.中心对称图形 一般地,在平面内,如果某个图形绕定点旋转180o后,得到的新图形和原图形重合,就说原图形是一个中心对称图形.定点是它的对称中心.或者说原图形具有中心对称性. 如图是一幅中心对称图形,O是对称中心,请找出点A绕点O旋转180后的对应点B.
点C的对应点B在哪?怎么找?
你能很快找出点E的对应点F吗?
中心对称的性质——中心对称图形上每一对对应点所连成的线段都被对称中心平分. 举例 线段是一个中心对称图形,对称中心是它的中点;平行四边形也是一个中心对称图形,对称中心是它的对角线交点,线段和平行四边形都具有中心对称性.探索活动—施罗德楼梯 如图中画的楼梯叫做施罗德楼梯(Schroder Stairs)
这幅画很简单,但是很奇妙:如果从右上角往左下角看,会觉得它是楼道里可以拾级而上的普通楼梯;可是,如果从左下角往右上角看,却会发现,图中画着天花板角落里的一段倒挂楼梯形装饰,可望而不可及. 像这样看在眼里能够引起幻觉的图形,叫做视幻图形.在现代面数设计中,被广泛应用来引起观众的兴趣.
下图中,显示了施罗德楼梯的中心对称结构.
想想看:怎样首先画出施罗德楼梯左下角的一篇阶梯墙壁?
怎样利用中心对称,进而画出右上角的阶梯形墙壁?
最后,怎样画出各级楼梯?
按照自己设想的步骤画画看,效果如何?灵活运用1.点的中心对称点的作法
以点O为对称中心,作出点A的中心对称点A'.
点A'即为所求的点.
2.线段的中心对称线段的作法
以点O为对称中心,作出线段AB的对称线段A'B'.谢谢指导!
点C的对应点B在哪?怎么找?
你能很快找出点E的对应点F吗?
中心对称的性质——中心对称图形上每一对对应点所连成的线段都被对称中心平分. 举例 线段是一个中心对称图形,对称中心是它的中点;平行四边形也是一个中心对称图形,对称中心是它的对角线交点,线段和平行四边形都具有中心对称性.探索活动—施罗德楼梯 如图中画的楼梯叫做施罗德楼梯(Schroder Stairs)
这幅画很简单,但是很奇妙:如果从右上角往左下角看,会觉得它是楼道里可以拾级而上的普通楼梯;可是,如果从左下角往右上角看,却会发现,图中画着天花板角落里的一段倒挂楼梯形装饰,可望而不可及. 像这样看在眼里能够引起幻觉的图形,叫做视幻图形.在现代面数设计中,被广泛应用来引起观众的兴趣.
下图中,显示了施罗德楼梯的中心对称结构.
想想看:怎样首先画出施罗德楼梯左下角的一篇阶梯墙壁?
怎样利用中心对称,进而画出右上角的阶梯形墙壁?
最后,怎样画出各级楼梯?
按照自己设想的步骤画画看,效果如何?灵活运用1.点的中心对称点的作法
以点O为对称中心,作出点A的中心对称点A'.
点A'即为所求的点.
2.线段的中心对称线段的作法
以点O为对称中心,作出线段AB的对称线段A'B'.谢谢指导!
同课章节目录
