2016秋北师大版九年级数学上册课件:4.5相似三角形判定定理的证明 (共13张PPT)
文档属性
| 名称 | 2016秋北师大版九年级数学上册课件:4.5相似三角形判定定理的证明 (共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 120.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 19:40:41 | ||
图片预览



文档简介
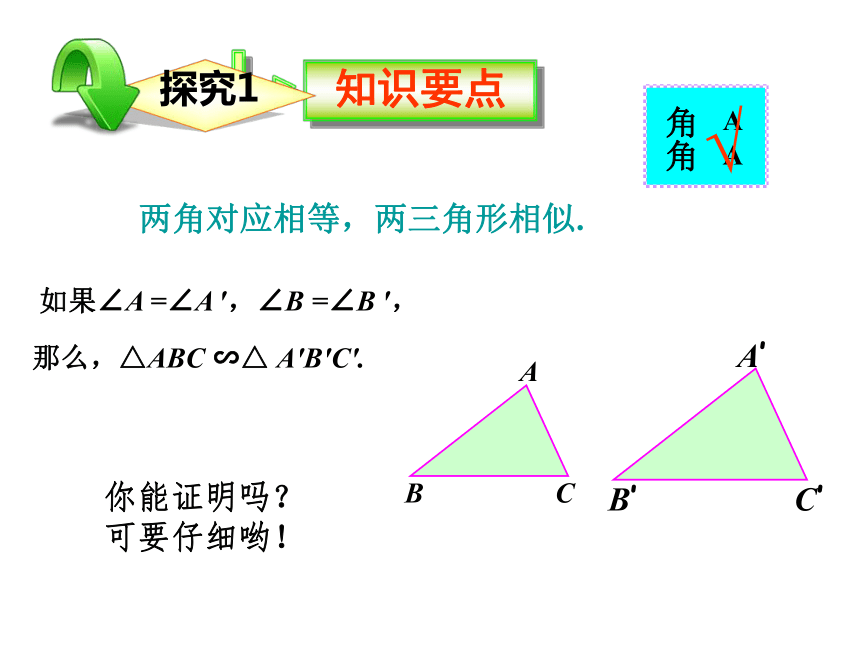
课件13张PPT。相似三角形判定定理的证明? 两角对应相等,两三角形相似.? 三边对应成比例,两三角形相似.相似三角形的判定方法:? 两边对应成比例且夹角相等,两三角形相似.回顾与复习两角对应相等,两三角形相似.那么,△ABC ∽△ A′B′C′.√如果∠A =∠A ′,∠B =∠B ′, 你能证明吗?可要仔细哟!解: ∵ ∠ A= ∠ A,∠ABD=∠C,
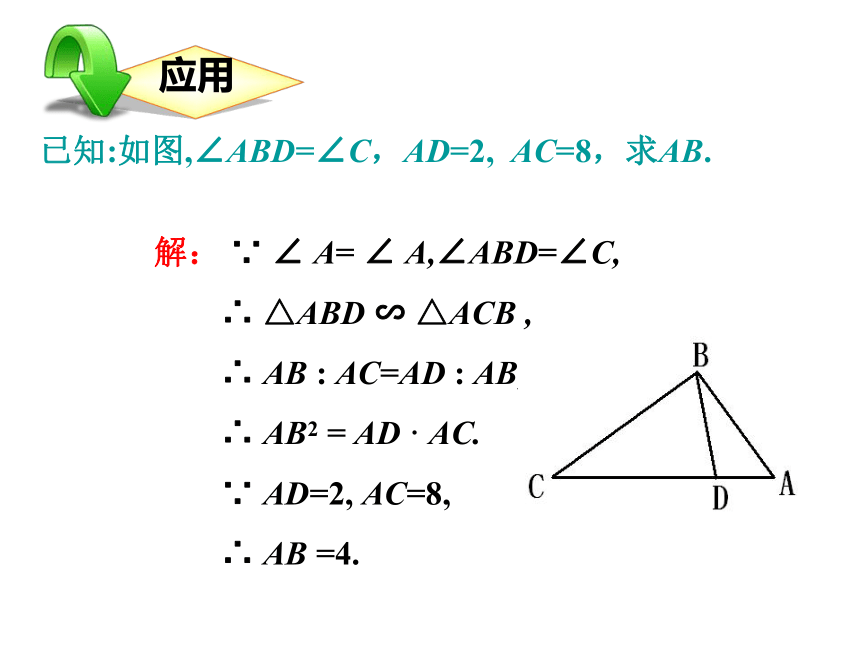
∴ △ABD ∽ △ACB ,
∴ AB : AC=AD : AB,
∴ AB2 = AD · AC.
∵ AD=2, AC=8,
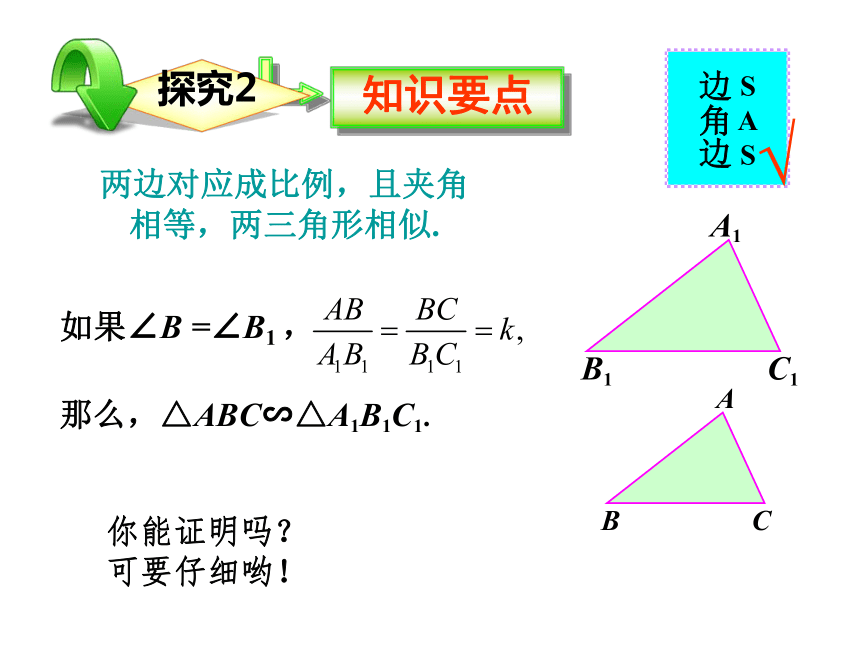
∴ AB =4.已知:如图,∠ABD=∠C,AD=2, AC=8,求AB. 两边对应成比例,且夹角相等,两三角形相似.√那么,△ABC∽△A1B1C1.如果∠B =∠B1 ,你能证明吗?可要仔细哟!不会如果这两个三角形一定会相似吗? 解:(1)∽两个三角形的相似比是多少?已知:如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD= ,求AD的长. 解: AB=6,BC=4,AC=5,CD= 又∠B=∠ACD,
△ABC∽△DCA,
AD=那么,△ABC∽△A′B′C′. 三边对应成比例,两三角形相似.√如果 任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同桌交流一下,看看是否有同样的结论.求证: △ . ∽△DE∴又∴同理 ∴∴∥∽∽∴∽∽例1 弦AB和CD相交于⊙O内一点P.
求证:PA·PB=PC·PD.ABCDPO证明:连接AC、BD.∵∠A、∠D都是CB所对的圆周角,⌒∴ ∠A=∠D.同理: ∠C=∠B.∴△PAC∽△PDB.即PA·PB=PC·PD.新知应用一、相似三角形判定定理的证明1.两角对应相等,两三角形相似.3.两边对应成比例且夹角相等,两三角形相似.二、相似三角形判定定理的应用2.三边对应成比例,两三角形相似.
∴ △ABD ∽ △ACB ,
∴ AB : AC=AD : AB,
∴ AB2 = AD · AC.
∵ AD=2, AC=8,
∴ AB =4.已知:如图,∠ABD=∠C,AD=2, AC=8,求AB. 两边对应成比例,且夹角相等,两三角形相似.√那么,△ABC∽△A1B1C1.如果∠B =∠B1 ,你能证明吗?可要仔细哟!不会如果这两个三角形一定会相似吗? 解:(1)∽两个三角形的相似比是多少?已知:如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD= ,求AD的长. 解: AB=6,BC=4,AC=5,CD= 又∠B=∠ACD,
△ABC∽△DCA,
AD=那么,△ABC∽△A′B′C′. 三边对应成比例,两三角形相似.√如果 任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同桌交流一下,看看是否有同样的结论.求证: △ . ∽△DE∴又∴同理 ∴∴∥∽∽∴∽∽例1 弦AB和CD相交于⊙O内一点P.
求证:PA·PB=PC·PD.ABCDPO证明:连接AC、BD.∵∠A、∠D都是CB所对的圆周角,⌒∴ ∠A=∠D.同理: ∠C=∠B.∴△PAC∽△PDB.即PA·PB=PC·PD.新知应用一、相似三角形判定定理的证明1.两角对应相等,两三角形相似.3.两边对应成比例且夹角相等,两三角形相似.二、相似三角形判定定理的应用2.三边对应成比例,两三角形相似.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
