苏教版高中数学选修3-4 4.4.2变换相乘.
文档属性
| 名称 | 苏教版高中数学选修3-4 4.4.2变换相乘. |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-23 08:45:42 | ||
图片预览






文档简介
课件16张PPT。§ 4.4.2 变换相乘1.连续作多次轴对称变换,有什么样的规律?
2.连续作多次中心对称变换?
3.连续作多次旋转变换?
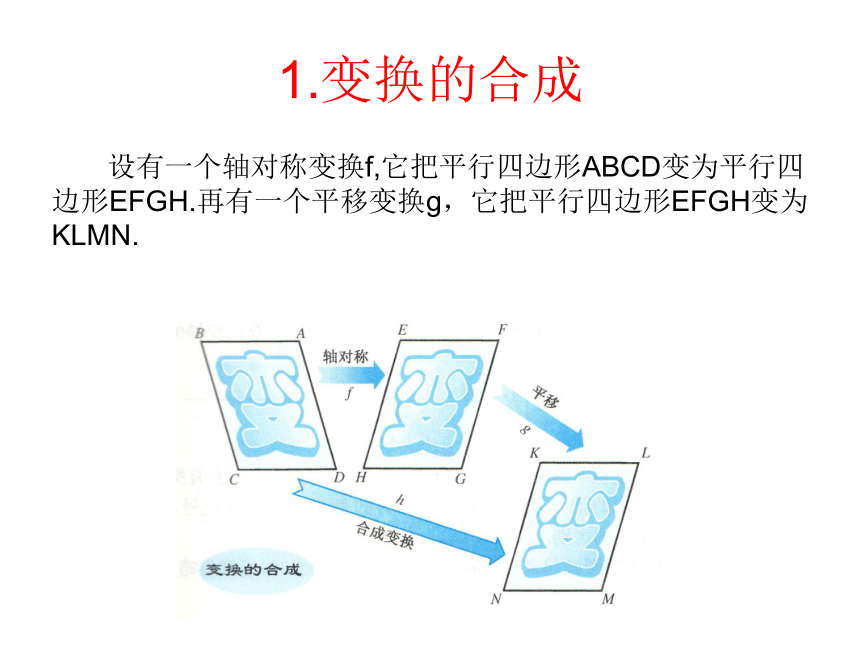
旧知回顾1.变换的合成 设有一个轴对称变换f,它把平行四边形ABCD变为平行四
边形EFGH.再有一个平移变换g,它把平行四边形EFGH变为
KLMN. 这样,顺次作两次变换f和g,从平行四边形ABCD
平行四边形EFGH 平行四边形KLMN
也可以看作从ABCD只经过一个变换h直达最终位置KLMN. 顺次作两个变换f和g,相当于作一个变换h,这样的变换h叫做变换f和g的合成变换.2.术语和记号 “先作变换f,然后作变换g,一变再变,结果等于直接作一个变换h”,可用记号简单表示为
g 。f = h
把合成变换h叫做变换f与变换g的乘积.
求合成变换的操作,叫变换的乘法. 就是仿照“九九八十一”这样的乘法口诀,“一扩再扩”推广成“一变再变”.是小圆圈 若写成 h=g 。f 意思就变成“变换h是由变换f与变换g合成的”.
h=g 。f 可以简写成h=gf.(小圆圈省略)
变换f与它自身的乘积,简写为f2=f 。f.
“一扩再扩”导致两数相乘,“一变再变”导致变换合成,后者是前者的一种推广.
虽然将变换的合成叫做“变换的乘法”,名称也叫“乘法”,含义却有发展,借用旧术语,赋予新含义.3.变换乘积实例汽车掉头
1、汽车向前方右转弯,旋转90o(变换f);
2、汽车向后方左转弯开倒车,旋转90o(变换g);
综合以上两步,汽车实现了在路面上将车身旋转180o(变换h),
这里,汽车掉头的变换h是旋转变换f与g的乘积,即h=gf.4.结合律 设有一连串三个任意变换f,g,h.又设A是平面内任意一点,变换f将A变到点B,变换g将B变到点C,变换h将C变到点D. 还可以看到一个从A到C的变换p,它是变换f与g的乘积(p=gf).还有一个从B到D的乘积q,是变换g与h的乘积(q=hg).
A B D(利用变换f和q,得qf);
A C D(利用变换p和h,得hp);
则有 qf=hp,
而 q=hg,p=gf,
所以 (hg)f=h(gf).
这样就证明了变换的乘法满足结合律:
对于任意三个变换f,g,h,必有(fg)f=h(gf). 任意一串三个变换f,g,h的连乘积,不管其中相邻变换怎样结合,连乘积总是同一个确定的变换l.
记为
l=hgf.
特例,n个相同变换f的连乘积,记为fn.5.逆变换 能将变位后图形中的所有各点全都恢复原位的变换g,叫做原变换f的逆变换.
换句话说,如果变换f的乘积是恒等变换e(gf=e),那么g叫做f的逆变换.记为f-1.
即
g=f-1.例
设变换f是绕点O逆时针旋转60o,那么它的逆变换f-1是绕点O顺时针转60o.
变换f是向南平移1km,那么它的逆变换f-1是向北平移1km.
如果变换f是轴对称,那么f的逆变换f-1就是f自己.
恒等变换e的逆变换还是恒等变换,即
e-1=e.1.变换的合成;
2.术语和记号;
3.结合律:对于任意三个变换f,g,h,必有(fg)f=h(gf).
4.逆变换谢谢指导!
2.连续作多次中心对称变换?
3.连续作多次旋转变换?
旧知回顾1.变换的合成 设有一个轴对称变换f,它把平行四边形ABCD变为平行四
边形EFGH.再有一个平移变换g,它把平行四边形EFGH变为
KLMN. 这样,顺次作两次变换f和g,从平行四边形ABCD
平行四边形EFGH 平行四边形KLMN
也可以看作从ABCD只经过一个变换h直达最终位置KLMN. 顺次作两个变换f和g,相当于作一个变换h,这样的变换h叫做变换f和g的合成变换.2.术语和记号 “先作变换f,然后作变换g,一变再变,结果等于直接作一个变换h”,可用记号简单表示为
g 。f = h
把合成变换h叫做变换f与变换g的乘积.
求合成变换的操作,叫变换的乘法. 就是仿照“九九八十一”这样的乘法口诀,“一扩再扩”推广成“一变再变”.是小圆圈 若写成 h=g 。f 意思就变成“变换h是由变换f与变换g合成的”.
h=g 。f 可以简写成h=gf.(小圆圈省略)
变换f与它自身的乘积,简写为f2=f 。f.
“一扩再扩”导致两数相乘,“一变再变”导致变换合成,后者是前者的一种推广.
虽然将变换的合成叫做“变换的乘法”,名称也叫“乘法”,含义却有发展,借用旧术语,赋予新含义.3.变换乘积实例汽车掉头
1、汽车向前方右转弯,旋转90o(变换f);
2、汽车向后方左转弯开倒车,旋转90o(变换g);
综合以上两步,汽车实现了在路面上将车身旋转180o(变换h),
这里,汽车掉头的变换h是旋转变换f与g的乘积,即h=gf.4.结合律 设有一连串三个任意变换f,g,h.又设A是平面内任意一点,变换f将A变到点B,变换g将B变到点C,变换h将C变到点D. 还可以看到一个从A到C的变换p,它是变换f与g的乘积(p=gf).还有一个从B到D的乘积q,是变换g与h的乘积(q=hg).
A B D(利用变换f和q,得qf);
A C D(利用变换p和h,得hp);
则有 qf=hp,
而 q=hg,p=gf,
所以 (hg)f=h(gf).
这样就证明了变换的乘法满足结合律:
对于任意三个变换f,g,h,必有(fg)f=h(gf). 任意一串三个变换f,g,h的连乘积,不管其中相邻变换怎样结合,连乘积总是同一个确定的变换l.
记为
l=hgf.
特例,n个相同变换f的连乘积,记为fn.5.逆变换 能将变位后图形中的所有各点全都恢复原位的变换g,叫做原变换f的逆变换.
换句话说,如果变换f的乘积是恒等变换e(gf=e),那么g叫做f的逆变换.记为f-1.
即
g=f-1.例
设变换f是绕点O逆时针旋转60o,那么它的逆变换f-1是绕点O顺时针转60o.
变换f是向南平移1km,那么它的逆变换f-1是向北平移1km.
如果变换f是轴对称,那么f的逆变换f-1就是f自己.
恒等变换e的逆变换还是恒等变换,即
e-1=e.1.变换的合成;
2.术语和记号;
3.结合律:对于任意三个变换f,g,h,必有(fg)f=h(gf).
4.逆变换谢谢指导!
同课章节目录
