苏教版高中数学选修3-4 4.5.1空间几何变换.
文档属性
| 名称 | 苏教版高中数学选修3-4 4.5.1空间几何变换. |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-23 00:00:00 | ||
图片预览






文档简介
课件14张PPT。§ 4.5.1 空间几何变换学习了平面图形的对称性,那么空间图形的呢?1.几种常见的空间变换(1)关于平面的对称变换(面反射)
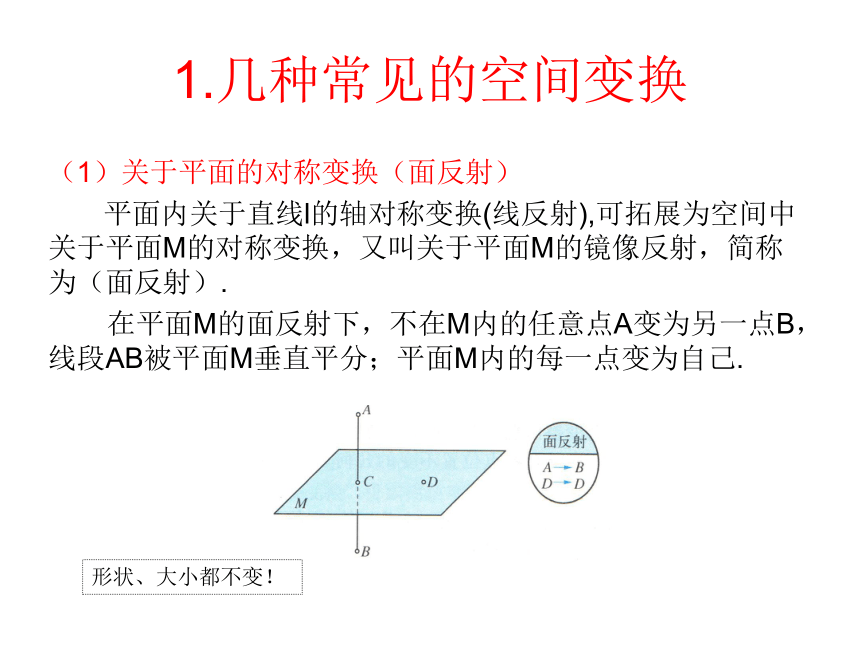
平面内关于直线l的轴对称变换(线反射),可拓展为空间中关于平面M的对称变换,又叫关于平面M的镜像反射,简称为(面反射).
在平面M的面反射下,不在M内的任意点A变为另一点B,线段AB被平面M垂直平分;平面M内的每一点变为自己.
形状、大小都不变!(2)中心对称变换(点反射)
平面内的中心对称变换,扩充为空间里的中心对称变换.
在空间中关于点O(对称中心)的中心对称变换下,不同于O的任意点P变为OP反向延长线上的点Q,使OQ=OP;点O变为它自己.
中心对称变换又叫做点反射.
点反射不改变图形的大小和形状.(3)绕直线的旋转变换
平面内绕一点A的旋转变换,扩展为空间中绕一直线a的旋转变换.
空间中,绕直线a沿某一方向旋转角θ的旋转变换F,限制到每个垂直于a的平面内,是绕垂足沿同一方向旋转角θ的平面旋转f.直线a称为变换F的旋转轴.
典例:房门绕垂直门轴的旋转.
绕直线旋转不改变图形的大小和形状.
(4)空间平移变换
平面内的平移变换,直接扩充为空间中的平移变换.
在空间中,沿着有向线段AB的平移变换将空间任意点P变到一点Q,使有向线段PQ与AB方向相同,长度相等.
空间平移变换不改变图形的形状和大小.(5)恒等变换
平面内的恒等变换可直接扩充到空间情形.
在空间中,保持所有各点位置不变的几何变换叫做恒等变换,记为e.
典例:时钟,设中午12时34分56秒的形状为空间图形甲,半夜12时34分56秒的形状为空间图形乙,那么图形乙中所有各点的位置都与图形甲中对应点的位置相同.因而,从图形甲到图形乙的几何变换是空间中的恒等变换.
一般地,对于绕直线的旋转,如果旋转角θ等于360o的整数倍,那么这样的特殊旋转就成为恒等变换,叫做平凡旋转.
(6)空间运动
平面运动开展为空间运动.
在空间中,如果一个几何变换不改变任意两点间的距离,就把这个变换叫做运动.
面反射、点反射、平移和绕直线旋转都是运动.在空间中,恒等变换也是一种运动,叫做平凡运动.2.空间对称图形 在空间中,如果几何变换f将某图形变换所得的新图形与原图形重合,就说原来的这个图形容许变换f.
例如:3片的风扇叶容许绕轴旋转120o.
几类最常见的空间对称图形是:面对称图形(容许面反射)、中心对称图形(容许点反射)、旋转对称图形(容许非平凡绕直线旋转)、平移对称图形(容许平移).例1 考虑任意平行六面体ABCD-A1B1C1D1,容易证明,它的四条对角AC1,BD1,CA1,DB1相交于统一点O,并且在点O互相平分.所以,关于点O的中心对称变换将这个平行六面体变为它自己,由此可见,任意平行六面体是中心对称图形,对角线交点O是它的对称中心. 例2 在空间中,线段AB是面对称图形,设线段AB的垂直平方面是M,那么关于平面M的面反射把线段AB变成它自己(线段端点A与B交换位置).
例3 二面角是平移对称图形,因为任意二面角容许沿着棱的方向的平移,二面角又是面对称图形,因为关于其分角面的镜像反射将这个二面角变成它自己.
例4 如果四面体的各棱长度互不相等,那么它不是对称图形.
因为它容许的唯一运动是恒等变换.谢谢指导!
平面内关于直线l的轴对称变换(线反射),可拓展为空间中关于平面M的对称变换,又叫关于平面M的镜像反射,简称为(面反射).
在平面M的面反射下,不在M内的任意点A变为另一点B,线段AB被平面M垂直平分;平面M内的每一点变为自己.
形状、大小都不变!(2)中心对称变换(点反射)
平面内的中心对称变换,扩充为空间里的中心对称变换.
在空间中关于点O(对称中心)的中心对称变换下,不同于O的任意点P变为OP反向延长线上的点Q,使OQ=OP;点O变为它自己.
中心对称变换又叫做点反射.
点反射不改变图形的大小和形状.(3)绕直线的旋转变换
平面内绕一点A的旋转变换,扩展为空间中绕一直线a的旋转变换.
空间中,绕直线a沿某一方向旋转角θ的旋转变换F,限制到每个垂直于a的平面内,是绕垂足沿同一方向旋转角θ的平面旋转f.直线a称为变换F的旋转轴.
典例:房门绕垂直门轴的旋转.
绕直线旋转不改变图形的大小和形状.
(4)空间平移变换
平面内的平移变换,直接扩充为空间中的平移变换.
在空间中,沿着有向线段AB的平移变换将空间任意点P变到一点Q,使有向线段PQ与AB方向相同,长度相等.
空间平移变换不改变图形的形状和大小.(5)恒等变换
平面内的恒等变换可直接扩充到空间情形.
在空间中,保持所有各点位置不变的几何变换叫做恒等变换,记为e.
典例:时钟,设中午12时34分56秒的形状为空间图形甲,半夜12时34分56秒的形状为空间图形乙,那么图形乙中所有各点的位置都与图形甲中对应点的位置相同.因而,从图形甲到图形乙的几何变换是空间中的恒等变换.
一般地,对于绕直线的旋转,如果旋转角θ等于360o的整数倍,那么这样的特殊旋转就成为恒等变换,叫做平凡旋转.
(6)空间运动
平面运动开展为空间运动.
在空间中,如果一个几何变换不改变任意两点间的距离,就把这个变换叫做运动.
面反射、点反射、平移和绕直线旋转都是运动.在空间中,恒等变换也是一种运动,叫做平凡运动.2.空间对称图形 在空间中,如果几何变换f将某图形变换所得的新图形与原图形重合,就说原来的这个图形容许变换f.
例如:3片的风扇叶容许绕轴旋转120o.
几类最常见的空间对称图形是:面对称图形(容许面反射)、中心对称图形(容许点反射)、旋转对称图形(容许非平凡绕直线旋转)、平移对称图形(容许平移).例1 考虑任意平行六面体ABCD-A1B1C1D1,容易证明,它的四条对角AC1,BD1,CA1,DB1相交于统一点O,并且在点O互相平分.所以,关于点O的中心对称变换将这个平行六面体变为它自己,由此可见,任意平行六面体是中心对称图形,对角线交点O是它的对称中心. 例2 在空间中,线段AB是面对称图形,设线段AB的垂直平方面是M,那么关于平面M的面反射把线段AB变成它自己(线段端点A与B交换位置).
例3 二面角是平移对称图形,因为任意二面角容许沿着棱的方向的平移,二面角又是面对称图形,因为关于其分角面的镜像反射将这个二面角变成它自己.
例4 如果四面体的各棱长度互不相等,那么它不是对称图形.
因为它容许的唯一运动是恒等变换.谢谢指导!
同课章节目录
