冀教版九年级数学上册同步练习卷《26.1 锐角三角函数(一)》(无答案)
文档属性
| 名称 | 冀教版九年级数学上册同步练习卷《26.1 锐角三角函数(一)》(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 52.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-23 07:34:56 | ||
图片预览

文档简介
《26.1
锐角三角函数(一)》
一、填空题
1.在Rt△ABC中,∠C=90°,AB=,BC=1,则tanB=______.
2.在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,若CD=18,AD=24,则tanB=______.
3.如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,则tanA=______=______,tanB=______=______,tan∠ACD=______,tan∠BCD=______.
4.如图,将以A为直角顶点的等腰直角三角形ABC沿直线BC平移得到△A′B′C′,使点B′与C重合,连接A′B,则tan∠A′BC′的值为______.
5.如果方程x2﹣4x+3=0的两个根分别是Rt△ABC的两条边,△ABC最小的角为A,那么tanA的值为______.
6.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=1,点D在AC上,将△ADB沿直线BD翻折后,将点A落在点E处,如果AD⊥ED,那么线段DE的长为______.
二、选择题
7.在Rt△ABC中,∠C=90°,tanA=,AC=4,则BC等于( )
A.
B.2
C.1
D.
8.在Rt△ABC中,∠C=90°,若各边都扩大了2倍,则tanA的数值( )
A.没有变化
B.扩大了2倍
C.缩小到
D.不能确定
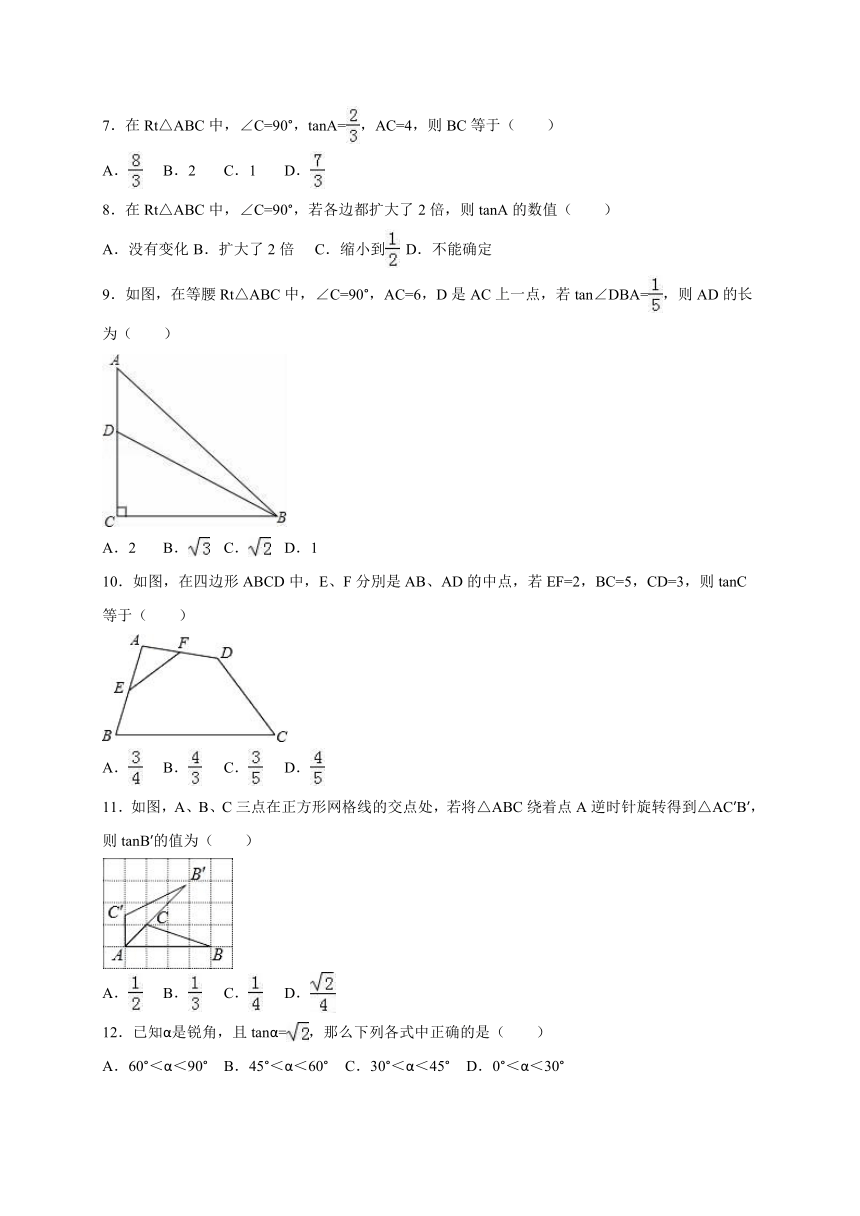
9.如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=,则AD的长为( )
A.2
B.
C.
D.1
10.如图,在四边形ABCD中,E、F分別是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于( )
A.
B.
C.
D.
11.如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( )
A.
B.
C.
D.
12.已知α是锐角,且tanα=,那么下列各式中正确的是( )
A.60°<α<90°
B.45°<α<60°
C.30°<α<45°
D.0°<α<30°
三、解答题
13.(6分)计算:
(1)tan245°+(1﹣)tan60°;
(2).
14.如图①、②分别表示甲、乙两个楼梯.
(1)求tanA、tanD的值;
(2)试比较两个楼梯中哪一个更陡?
15.如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作cotα,即cotα==.根据上述角的余切定义,解下列问题:
(1)cot30°=______;
(2)如图,已知tanA=,其中∠A为锐角,试求cotA的值.
16.如图,已知正方形ABCD的边长为2,若将线段BD绕点B旋转后,点D落在CB的延长线上的D′处,试求tan∠BAD′的值.
17.如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.
(1)求证:AB=DF;
(2)若AD=10,AB=6,求tan∠EDF的值.
18.如图,在Rt△ABC中,∠C=90°,D是BC的中点,DE⊥AB于E,tanB=,且AE=6,求DE的长.
锐角三角函数(一)》
一、填空题
1.在Rt△ABC中,∠C=90°,AB=,BC=1,则tanB=______.
2.在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,若CD=18,AD=24,则tanB=______.
3.如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,则tanA=______=______,tanB=______=______,tan∠ACD=______,tan∠BCD=______.
4.如图,将以A为直角顶点的等腰直角三角形ABC沿直线BC平移得到△A′B′C′,使点B′与C重合,连接A′B,则tan∠A′BC′的值为______.
5.如果方程x2﹣4x+3=0的两个根分别是Rt△ABC的两条边,△ABC最小的角为A,那么tanA的值为______.
6.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=1,点D在AC上,将△ADB沿直线BD翻折后,将点A落在点E处,如果AD⊥ED,那么线段DE的长为______.
二、选择题
7.在Rt△ABC中,∠C=90°,tanA=,AC=4,则BC等于( )
A.
B.2
C.1
D.
8.在Rt△ABC中,∠C=90°,若各边都扩大了2倍,则tanA的数值( )
A.没有变化
B.扩大了2倍
C.缩小到
D.不能确定
9.如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=,则AD的长为( )
A.2
B.
C.
D.1
10.如图,在四边形ABCD中,E、F分別是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于( )
A.
B.
C.
D.
11.如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( )
A.
B.
C.
D.
12.已知α是锐角,且tanα=,那么下列各式中正确的是( )
A.60°<α<90°
B.45°<α<60°
C.30°<α<45°
D.0°<α<30°
三、解答题
13.(6分)计算:
(1)tan245°+(1﹣)tan60°;
(2).
14.如图①、②分别表示甲、乙两个楼梯.
(1)求tanA、tanD的值;
(2)试比较两个楼梯中哪一个更陡?
15.如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作cotα,即cotα==.根据上述角的余切定义,解下列问题:
(1)cot30°=______;
(2)如图,已知tanA=,其中∠A为锐角,试求cotA的值.
16.如图,已知正方形ABCD的边长为2,若将线段BD绕点B旋转后,点D落在CB的延长线上的D′处,试求tan∠BAD′的值.
17.如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.
(1)求证:AB=DF;
(2)若AD=10,AB=6,求tan∠EDF的值.
18.如图,在Rt△ABC中,∠C=90°,D是BC的中点,DE⊥AB于E,tanB=,且AE=6,求DE的长.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
