人教版九年级数学上册同步练习卷《23.3 课题学习 图案设计》(无答案)
文档属性
| 名称 | 人教版九年级数学上册同步练习卷《23.3 课题学习 图案设计》(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 107.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-23 07:36:09 | ||
图片预览



文档简介
23.3
课题学习
图案设计
一、选择题(共5小题)
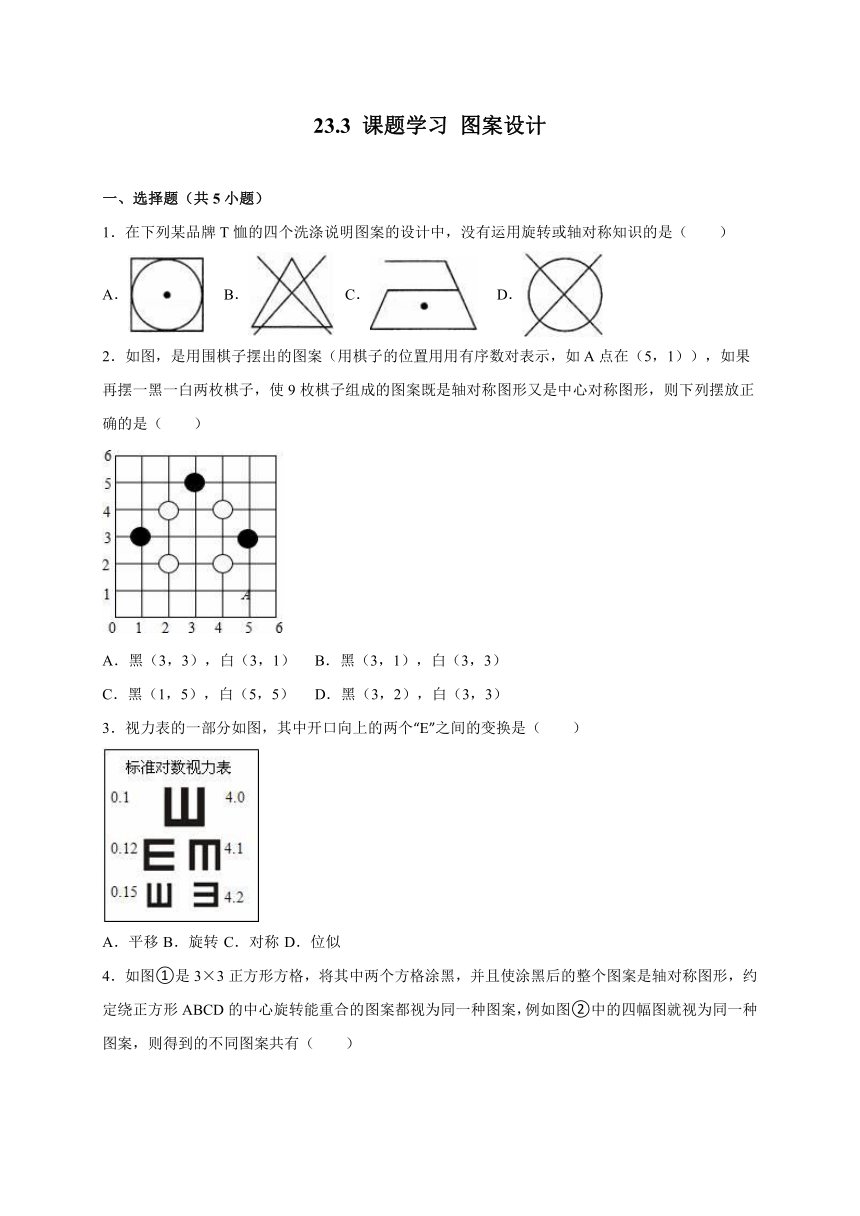
1.在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是( )
A.
B.
C.
D.
2.如图,是用围棋子摆出的图案(用棋子的位置用用有序数对表示,如A点在(5,1)),如果再摆一黑一白两枚棋子,使9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )
A.黑(3,3),白(3,1)
B.黑(3,1),白(3,3)
C.黑(1,5),白(5,5)
D.黑(3,2),白(3,3)
3.视力表的一部分如图,其中开口向上的两个“E”之间的变换是( )
A.平移
B.旋转
C.对称
D.位似
4.如图①是3×3正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,约定绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图②中的四幅图就视为同一种图案,则得到的不同图案共有( )
A.4种
B.5种
C.6种
D.7种
5.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种
B.3种
C.4种
D.5种
二、填空题(共4小题)
6.以如图(1)(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换能得到图(2)的有______(只填序号,多填或错填得0分,少填个酌情给分).
①只要向右平移1个单位;
②先以直线AB为对称轴进行翻折,再向右平移1个单位;
③先绕着点O旋转180°,再向右平移一个单位;
④绕着OB的中点旋转180°即可.
7.如图,是一个4×4的正方形网格,每个小正方形的边长为1.请你在网格中以左上角的三角形为基本图形,通过平移、对称或旋转变换,设计一个精美图案,使其满足:
①既是轴对称图形,又是以点O为对称中心的中心对称图形;
②所作图案用阴影标识,且阴影部分面积为4.
8.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,涂黑的小正方形的序号是______.
9.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有______种.
三、解答题(共6小题)
10.阅读以下材料,并按要求完成相应的任务.
几何中,平行四边形、矩形、菱形、正方形和等腰梯形都是特殊的四边形,大家对于它们的性质都非常熟悉,生活中还有一种特殊的四边形﹣﹣筝形.所谓筝形,它的形状与我们生活中风筝的骨架相似.定义:两组邻边分别相等的四边形,称之为筝形,如图,四边形ABCD是筝形,其中AB=AD,CB=CD判定:①两组邻边分别相等的四边形是筝形②有一条对角线垂直平分另一条对角线的四边形是筝形显然,菱形是特殊的筝形,就一般筝形而言,它与菱形有许多相同点和不同点
如果只研究一般的筝形(不包括菱形),请根据以上材料完成下列任务:
(1)请说出筝形和菱形的相同点和不同点各两条;
(2)请仿照图1的画法,在图2所示的8×8网格中重新设计一个由四个全等的筝形和四个全等的菱形组成的新图案,具体要求如下:
①顶点都在格点上;
②所设计的图案既是轴对称图形又是中心对称图形;
③将新图案中的四个筝形都涂上阴影(建议用一系列平行斜线表示阴影).
11.在数学活动课上,王老师发给每位同学一张半径为6个单位长度的圆形纸板,要求同学们:
(1)从带刻度的三角板、量角器和圆规三种作图工具中任意选取作图工具,把圆形纸板分成面积相等的四部分;
(2)设计的整个图案是某种对称图形.
王老师给出了方案一,请你用所学的知识再设计两种方案,并完成下面的设计报告.
名
称
四等分圆的面积
方
案
方案一
方案二
方案三
选用的工具
带刻度的三角板
画出示意图
简述设计方案
作⊙O两条互相垂直的直径AB、CD,将⊙O的面积分成相等的四份.
指出对称性
既是轴对称图形又是中心对称图形
12.利用对称变换可设计出美丽图案,如图,在方格纸中每一个顶点都在格点上的四边形,且每个小正方形的边长都为1,完成下列问题:
(1)图案设计:先作出四边形关于直线l成轴对称的图形,再将你所作的图形和原四边形绕0点按顺时针旋转90°;
(2)完成上述图案设计后,可知这个图案的面积等于______.
13.如图,已知A(﹣3,﹣3),B(﹣2,﹣1),C(﹣1,﹣2)是直角坐标平面上三点.
(1)请画出△ABC关于原点O对称的△A1B1C1;
(2)请写出点B关于y轴对称的点B2的坐标,若将点B2向上平移h个单位,使其落在△A1B1C1内部,指出h的取值范围.
14.在格纸上按以下要求作图,不用写作法:
(1)作出“小旗子”向右平移6格后的图案;
(2)作出“小旗子”绕O点按逆时针方向旋转90°后的图案.
15.如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).
(1)先将Rt△ABC向左平移5个单位长度,再向下平移1个单位长度得到Rt△A1B1C1,试在图中画出Rt△A1B1C1,并写出点A1的坐标;
(2)再将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2,试在图中画出Rt△A2B2C2,并计算Rt△A1B1C1在上述旋转过程中点C1所经过的路径长.
课题学习
图案设计
一、选择题(共5小题)
1.在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是( )
A.
B.
C.
D.
2.如图,是用围棋子摆出的图案(用棋子的位置用用有序数对表示,如A点在(5,1)),如果再摆一黑一白两枚棋子,使9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )
A.黑(3,3),白(3,1)
B.黑(3,1),白(3,3)
C.黑(1,5),白(5,5)
D.黑(3,2),白(3,3)
3.视力表的一部分如图,其中开口向上的两个“E”之间的变换是( )
A.平移
B.旋转
C.对称
D.位似
4.如图①是3×3正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,约定绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图②中的四幅图就视为同一种图案,则得到的不同图案共有( )
A.4种
B.5种
C.6种
D.7种
5.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种
B.3种
C.4种
D.5种
二、填空题(共4小题)
6.以如图(1)(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换能得到图(2)的有______(只填序号,多填或错填得0分,少填个酌情给分).
①只要向右平移1个单位;
②先以直线AB为对称轴进行翻折,再向右平移1个单位;
③先绕着点O旋转180°,再向右平移一个单位;
④绕着OB的中点旋转180°即可.
7.如图,是一个4×4的正方形网格,每个小正方形的边长为1.请你在网格中以左上角的三角形为基本图形,通过平移、对称或旋转变换,设计一个精美图案,使其满足:
①既是轴对称图形,又是以点O为对称中心的中心对称图形;
②所作图案用阴影标识,且阴影部分面积为4.
8.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,涂黑的小正方形的序号是______.
9.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有______种.
三、解答题(共6小题)
10.阅读以下材料,并按要求完成相应的任务.
几何中,平行四边形、矩形、菱形、正方形和等腰梯形都是特殊的四边形,大家对于它们的性质都非常熟悉,生活中还有一种特殊的四边形﹣﹣筝形.所谓筝形,它的形状与我们生活中风筝的骨架相似.定义:两组邻边分别相等的四边形,称之为筝形,如图,四边形ABCD是筝形,其中AB=AD,CB=CD判定:①两组邻边分别相等的四边形是筝形②有一条对角线垂直平分另一条对角线的四边形是筝形显然,菱形是特殊的筝形,就一般筝形而言,它与菱形有许多相同点和不同点
如果只研究一般的筝形(不包括菱形),请根据以上材料完成下列任务:
(1)请说出筝形和菱形的相同点和不同点各两条;
(2)请仿照图1的画法,在图2所示的8×8网格中重新设计一个由四个全等的筝形和四个全等的菱形组成的新图案,具体要求如下:
①顶点都在格点上;
②所设计的图案既是轴对称图形又是中心对称图形;
③将新图案中的四个筝形都涂上阴影(建议用一系列平行斜线表示阴影).
11.在数学活动课上,王老师发给每位同学一张半径为6个单位长度的圆形纸板,要求同学们:
(1)从带刻度的三角板、量角器和圆规三种作图工具中任意选取作图工具,把圆形纸板分成面积相等的四部分;
(2)设计的整个图案是某种对称图形.
王老师给出了方案一,请你用所学的知识再设计两种方案,并完成下面的设计报告.
名
称
四等分圆的面积
方
案
方案一
方案二
方案三
选用的工具
带刻度的三角板
画出示意图
简述设计方案
作⊙O两条互相垂直的直径AB、CD,将⊙O的面积分成相等的四份.
指出对称性
既是轴对称图形又是中心对称图形
12.利用对称变换可设计出美丽图案,如图,在方格纸中每一个顶点都在格点上的四边形,且每个小正方形的边长都为1,完成下列问题:
(1)图案设计:先作出四边形关于直线l成轴对称的图形,再将你所作的图形和原四边形绕0点按顺时针旋转90°;
(2)完成上述图案设计后,可知这个图案的面积等于______.
13.如图,已知A(﹣3,﹣3),B(﹣2,﹣1),C(﹣1,﹣2)是直角坐标平面上三点.
(1)请画出△ABC关于原点O对称的△A1B1C1;
(2)请写出点B关于y轴对称的点B2的坐标,若将点B2向上平移h个单位,使其落在△A1B1C1内部,指出h的取值范围.
14.在格纸上按以下要求作图,不用写作法:
(1)作出“小旗子”向右平移6格后的图案;
(2)作出“小旗子”绕O点按逆时针方向旋转90°后的图案.
15.如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).
(1)先将Rt△ABC向左平移5个单位长度,再向下平移1个单位长度得到Rt△A1B1C1,试在图中画出Rt△A1B1C1,并写出点A1的坐标;
(2)再将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2,试在图中画出Rt△A2B2C2,并计算Rt△A1B1C1在上述旋转过程中点C1所经过的路径长.
同课章节目录
