用待定系数法求二次函数的解析式
图片预览


文档简介
课件11张PPT。用待定系数法求二次函数的解析式yx课 前 复 习思考二次函数解析式有哪几种表达式? 一般式:y=ax2+bx+c 顶点式:y=a(x-h)2+k
两根式:y=a(x-x1)(x-x2)例题封面例 题 选 讲一般式: y=ax2+bx+c两根式:
y=a(x-x1)(x-x2)顶点式:
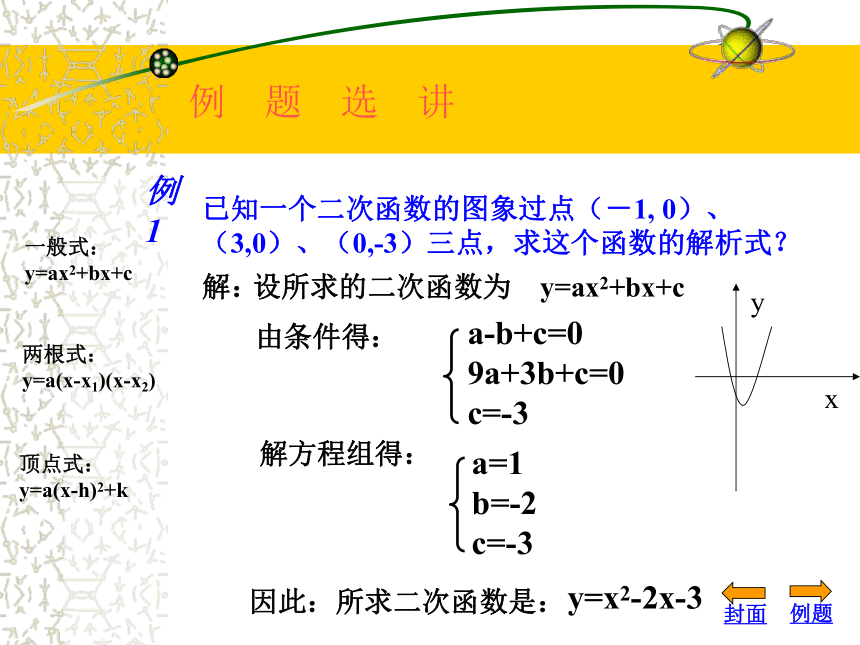
y=a(x-h)2+k解:设所求的二次函数为 y=ax2+bx+c由条件得:a-b+c=0
9a+3b+c=0
c=-3解方程组得:因此:所求二次函数是: a=1
b=-2
c=-3y=x2-2x-3例1例题封面x例 题 选 讲一般式: y=ax2+bx+c两根式:
y=a(x-x1)(x-x2)顶点式:
y=a(x-h)2+k解:设所求的二次函数为y=a(x+1)(x-3) 把 点 ( 0,-3)代入y=a(x+1)(x-3)
得:a(0+1)(0-3)=-3因此:所求二次函数是:y= (x+1)(x-3)
得: a=1即y=x2-2x-3已知一个二次函数的图象过点(-1, 0)、
(3,0)、(0,-3)三点,求这个函数的解析式?y例1例题封面x例 题 选 讲一般式: y=ax2+bx+c两根式:
y=a(x-x1)(x-x2)顶点式:
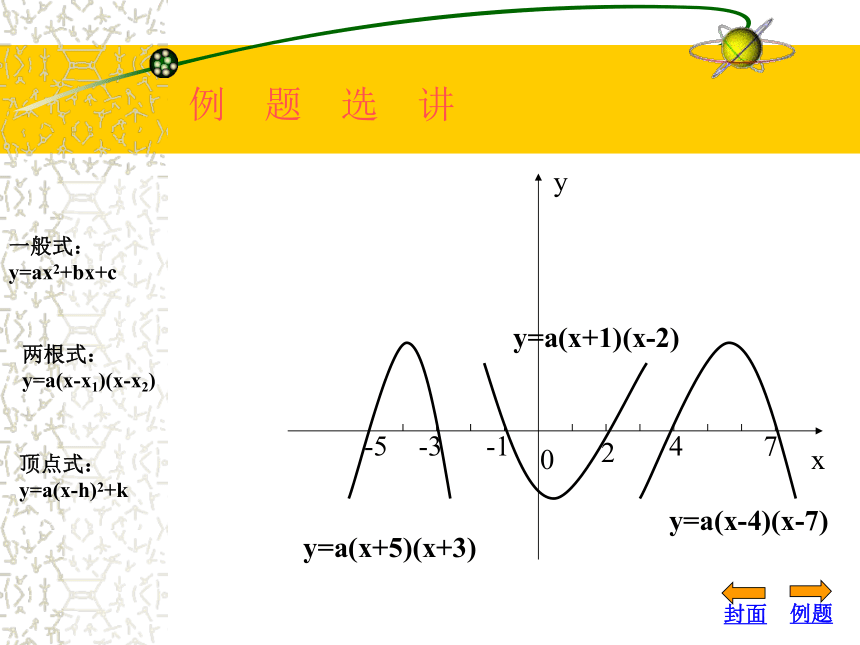
y=a(x-h)2+k例题封面y=a(x+5)(x+3)
y=a(x+1)(x-2)
y=a(x-4)(x-7)
xy0-5-3-1247例 题 选 讲解:设所求的二次函数为 y=a(x+1)2-3由条件得:点( 0,-5 )在抛物线上a-3=-5, 得a=-2故所求的抛物线解析式为 y=-2(x+1)2-3即:y=-2x2-4x-5
一般式: y=ax2+bx+c两根式:
y=a(x-x1)(x-x2)顶点式:
y=a(x-h)2+k例2例题封面例 题 选 讲一般式: y=ax2+bx+c两根式:
y=a(x-x1)(x-x2)顶点式:
y=a(x-h)2+k例题封面
y=a(x+2)2+2y=a(x-3)2+3xy0-5-3-1247-2233y=a(x+2)2-2
一场篮球赛中,小明跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米。 问此球能否投中?3米8米4米4米0投篮问题:03xy(0,3)小明的出手高度为3m时
能将篮球投入篮圈03xy(7,3)y小明朝着篮球架再向前平移1m
后跳起投篮也能将篮球投入篮圈作业布置:补充练习
两根式:y=a(x-x1)(x-x2)例题封面例 题 选 讲一般式: y=ax2+bx+c两根式:
y=a(x-x1)(x-x2)顶点式:
y=a(x-h)2+k解:设所求的二次函数为 y=ax2+bx+c由条件得:a-b+c=0
9a+3b+c=0
c=-3解方程组得:因此:所求二次函数是: a=1
b=-2
c=-3y=x2-2x-3例1例题封面x例 题 选 讲一般式: y=ax2+bx+c两根式:
y=a(x-x1)(x-x2)顶点式:
y=a(x-h)2+k解:设所求的二次函数为y=a(x+1)(x-3) 把 点 ( 0,-3)代入y=a(x+1)(x-3)
得:a(0+1)(0-3)=-3因此:所求二次函数是:y= (x+1)(x-3)
得: a=1即y=x2-2x-3已知一个二次函数的图象过点(-1, 0)、
(3,0)、(0,-3)三点,求这个函数的解析式?y例1例题封面x例 题 选 讲一般式: y=ax2+bx+c两根式:
y=a(x-x1)(x-x2)顶点式:
y=a(x-h)2+k例题封面y=a(x+5)(x+3)
y=a(x+1)(x-2)
y=a(x-4)(x-7)
xy0-5-3-1247例 题 选 讲解:设所求的二次函数为 y=a(x+1)2-3由条件得:点( 0,-5 )在抛物线上a-3=-5, 得a=-2故所求的抛物线解析式为 y=-2(x+1)2-3即:y=-2x2-4x-5
一般式: y=ax2+bx+c两根式:
y=a(x-x1)(x-x2)顶点式:
y=a(x-h)2+k例2例题封面例 题 选 讲一般式: y=ax2+bx+c两根式:
y=a(x-x1)(x-x2)顶点式:
y=a(x-h)2+k例题封面
y=a(x+2)2+2y=a(x-3)2+3xy0-5-3-1247-2233y=a(x+2)2-2
一场篮球赛中,小明跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米。 问此球能否投中?3米8米4米4米0投篮问题:03xy(0,3)小明的出手高度为3m时
能将篮球投入篮圈03xy(7,3)y小明朝着篮球架再向前平移1m
后跳起投篮也能将篮球投入篮圈作业布置:补充练习
