向量减法
图片预览





文档简介
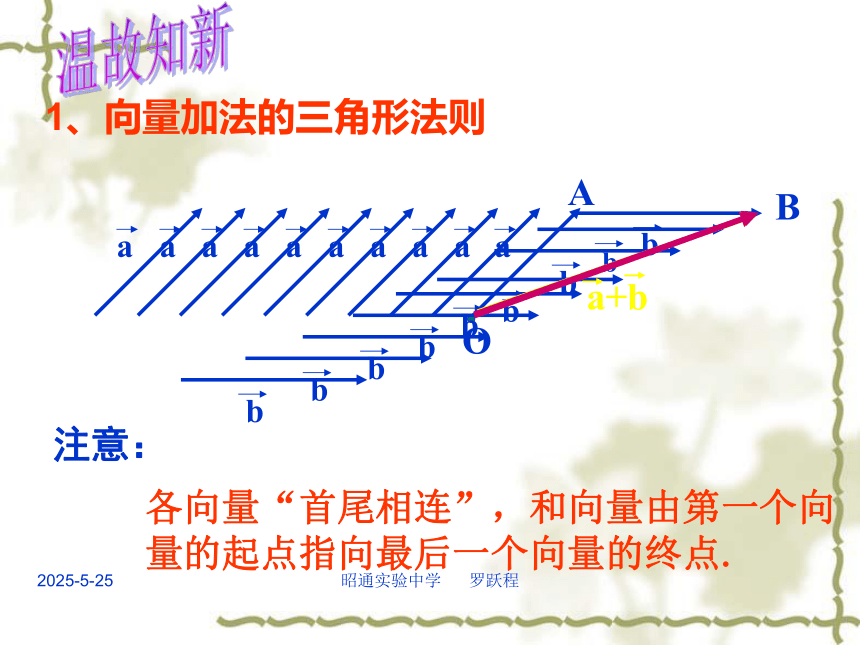
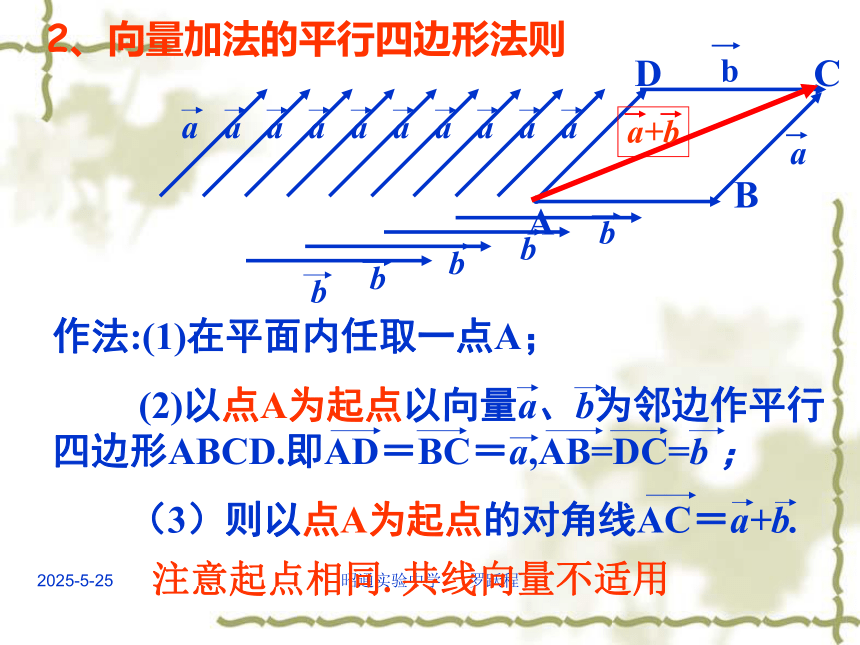
课件21张PPT。2019/3/10昭通实验中学 罗跃程2.2.2向量的减法教而不研则浅研而不教则空欢迎各位领导和老师的到来,你们的到来,是116班全体同学的荣幸。2019/3/10昭通实验中学 罗跃程1、向量加法的三角形法则注意:各向量“首尾相连”,和向量由第一个向量的起点指向最后一个向量的终点.温故知新2019/3/10昭通实验中学 罗跃程2、向量加法的平行四边形法则注意起点相同.共线向量不适用
2019/3/10昭通实验中学 罗跃程走进新课 我们曾经学习过减去一个数等于加上这个数的相反数。前面又学习了向量加法,而加与减是对立统一的两个方面,既然向量可以相加,那自然也可以相减.因此,两个向量如何进行减法运算,就成为研究的必然.
2019/3/10昭通实验中学 罗跃程探究一:向量减法的含义思考2:向量a的相反向量可以怎样表示?
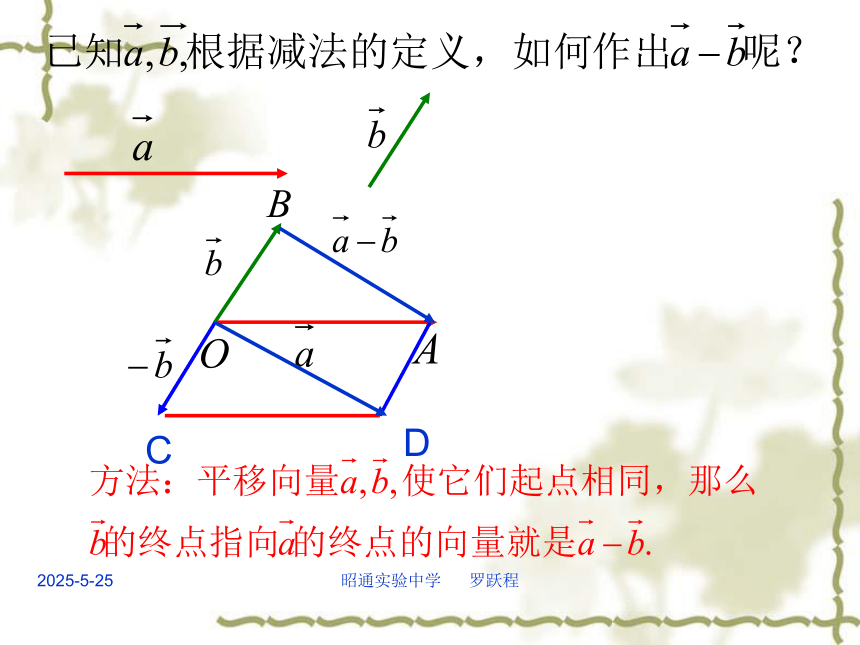
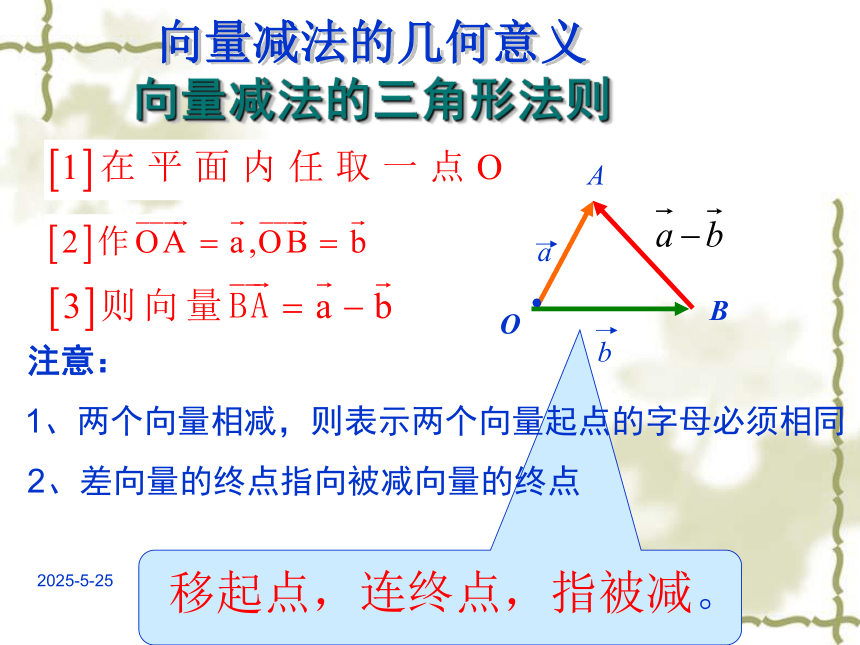
两个相反向量的和向量是什么?-a思考1:什么是相等向量?怎样定义相反向量?大小相等,方向相同的向量,叫相等向量。大小相等,方向相反的向量,叫相反向量。AB 与 BA是否互为相反向量?是(-a)+a=02019/3/10昭通实验中学 罗跃程思考3:-a的相反向量是什么?零向量的相反向量是什么?规定:零向量的相反向量仍是零向量.-(-a)=a2019/3/10昭通实验中学 罗跃程思考4:在实数的运算中,减去一个数等于加上这个数的相反数.据此原理,向量a-b可以怎样理解?求两个向量的差的运算叫做向量的减法.定义:a-b= a +(-b).2019/3/10昭通实验中学 罗跃程CD2019/3/10昭通实验中学 罗跃程向量减法的几何意义 向量减法的三角形法则OAB. 注意:
1、两个向量相减,则表示两个向量起点的字母必须相同
2、差向量的终点指向被减向量的终点移起点,连终点,指被减。2019/3/10昭通实验中学 罗跃程探究(二):向量减法的几何意义思考1:如果向量a与b同向,如何作出向量a-b?思考2:如果向量a与b反向,如何作出向量a-b?2019/3/10昭通实验中学 罗跃程练习2019/3/10昭通实验中学 罗跃程例1:如图,已知向量
求作向量 2019/3/10昭通实验中学 罗跃程OABCD2019/3/10昭通实验中学 罗跃程例3:如图,平行四边形ABCD,AB=a,AD=b,用a、b表示向量AC、DB。ADBCab注意向量的方向,向量AC=a+b,向量DB=a-b变式一:当a, b满足什么条件时,a+b与a?b垂直? 变式二:当a, b满足什么条件时,|a+b| = |a?b|? 变式三:a+b与a?b可能是相等向量吗? 变式四:证明:,并说明什么时候取等号?2019/3/10昭通实验中学 罗跃程2019/3/10昭通实验中学 罗跃程练习2019/3/10昭通实验中学 罗跃程O`2019/3/10昭通实验中学 罗跃程O`return2019/3/10昭通实验中学 罗跃程本节课你学到了什么?相反向量的概念,及其应用;(向量减法的三角形法则);解决向量加法,减法问题,数形结合必不可少.向量减法的定义,及其运算法则;2019/3/10昭通实验中学 罗跃程作业:习题2.2,p91 4.(4),(5),(6),(7). 5, 7, 82019/3/10昭通实验中学 罗跃程谢谢各位老师光临指导!祝同学们学习进步!再见
2019/3/10昭通实验中学 罗跃程走进新课 我们曾经学习过减去一个数等于加上这个数的相反数。前面又学习了向量加法,而加与减是对立统一的两个方面,既然向量可以相加,那自然也可以相减.因此,两个向量如何进行减法运算,就成为研究的必然.
2019/3/10昭通实验中学 罗跃程探究一:向量减法的含义思考2:向量a的相反向量可以怎样表示?
两个相反向量的和向量是什么?-a思考1:什么是相等向量?怎样定义相反向量?大小相等,方向相同的向量,叫相等向量。大小相等,方向相反的向量,叫相反向量。AB 与 BA是否互为相反向量?是(-a)+a=02019/3/10昭通实验中学 罗跃程思考3:-a的相反向量是什么?零向量的相反向量是什么?规定:零向量的相反向量仍是零向量.-(-a)=a2019/3/10昭通实验中学 罗跃程思考4:在实数的运算中,减去一个数等于加上这个数的相反数.据此原理,向量a-b可以怎样理解?求两个向量的差的运算叫做向量的减法.定义:a-b= a +(-b).2019/3/10昭通实验中学 罗跃程CD2019/3/10昭通实验中学 罗跃程向量减法的几何意义 向量减法的三角形法则OAB. 注意:
1、两个向量相减,则表示两个向量起点的字母必须相同
2、差向量的终点指向被减向量的终点移起点,连终点,指被减。2019/3/10昭通实验中学 罗跃程探究(二):向量减法的几何意义思考1:如果向量a与b同向,如何作出向量a-b?思考2:如果向量a与b反向,如何作出向量a-b?2019/3/10昭通实验中学 罗跃程练习2019/3/10昭通实验中学 罗跃程例1:如图,已知向量
求作向量 2019/3/10昭通实验中学 罗跃程OABCD2019/3/10昭通实验中学 罗跃程例3:如图,平行四边形ABCD,AB=a,AD=b,用a、b表示向量AC、DB。ADBCab注意向量的方向,向量AC=a+b,向量DB=a-b变式一:当a, b满足什么条件时,a+b与a?b垂直? 变式二:当a, b满足什么条件时,|a+b| = |a?b|? 变式三:a+b与a?b可能是相等向量吗? 变式四:证明:,并说明什么时候取等号?2019/3/10昭通实验中学 罗跃程2019/3/10昭通实验中学 罗跃程练习2019/3/10昭通实验中学 罗跃程O`2019/3/10昭通实验中学 罗跃程O`return2019/3/10昭通实验中学 罗跃程本节课你学到了什么?相反向量的概念,及其应用;(向量减法的三角形法则);解决向量加法,减法问题,数形结合必不可少.向量减法的定义,及其运算法则;2019/3/10昭通实验中学 罗跃程作业:习题2.2,p91 4.(4),(5),(6),(7). 5, 7, 82019/3/10昭通实验中学 罗跃程谢谢各位老师光临指导!祝同学们学习进步!再见
