北师大版八年级数学上册同步测试《2.6 实数》(无答案)
文档属性
| 名称 | 北师大版八年级数学上册同步测试《2.6 实数》(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 48.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-23 18:41:24 | ||
图片预览

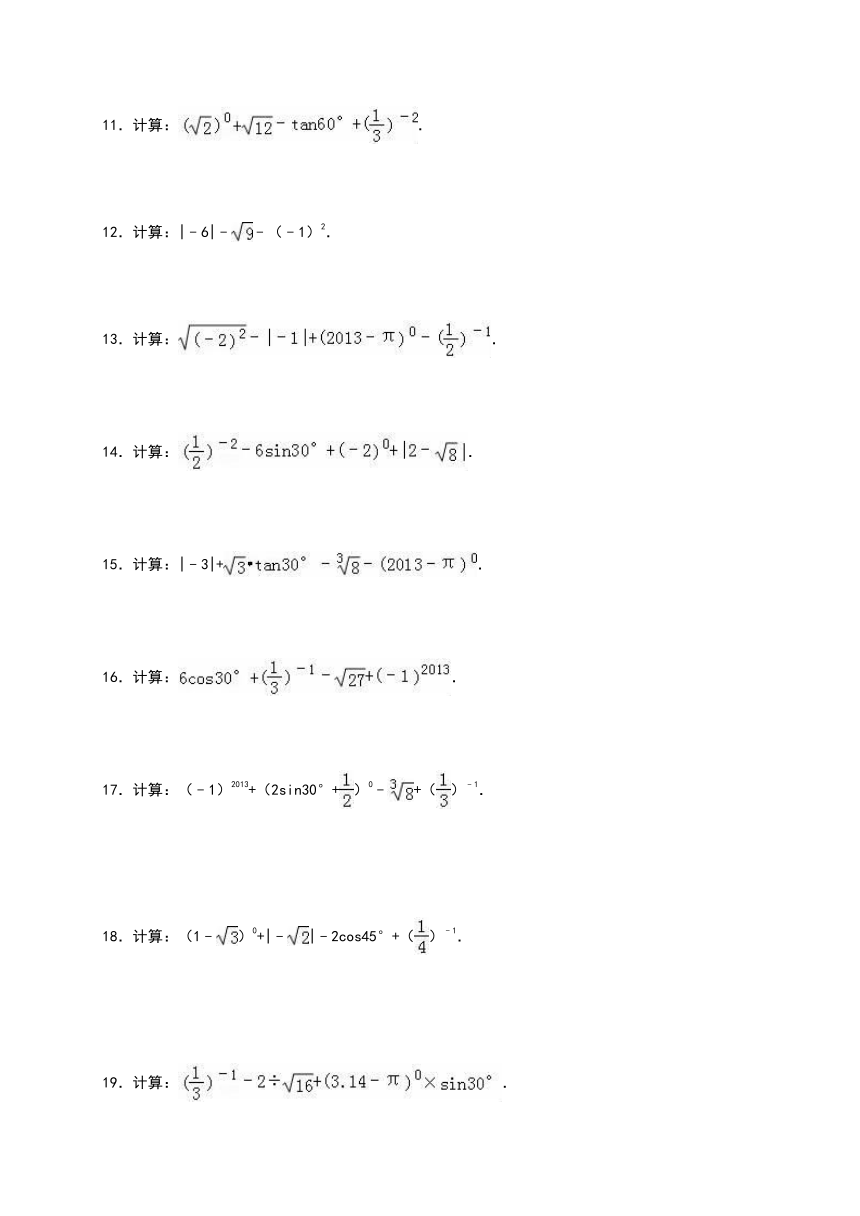
文档简介
2.6
实数
一、填空题
1.我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2 i=(﹣1) i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4n i=(i4)n i=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013的值为______.
2.计算:|1﹣|+﹣(3.14﹣π)0﹣(﹣)﹣1=______.
3.计算:
=______.
4.计算:
=______.
5.对于实数a、b,定义运算 如下:a b=,例如,2 4=2﹣4=.计算[2 2]×[(﹣3) 2]=______.
6.计算:
=______.
二、计算题
7.计算:(﹣2)2﹣()0.
8.计算:(1﹣)0﹣+2sin60°﹣|﹣|
9.计算:|﹣|+(2013﹣)0﹣()﹣1﹣2sin60°.
10.计算:
+|﹣3|﹣(π﹣2013)0.
11.计算:.
12.计算:|﹣6|﹣﹣(﹣1)2.
13.计算:.
14.计算:.
15.计算:|﹣3|+.
16.计算:.
17.计算:(﹣1)2013+(2sin30°+)0﹣+()﹣1.
18.计算:(1﹣)0+|﹣|﹣2cos45°+()﹣1.
19.计算:.
20.计算:.
21.计算:.
22.计算:(﹣3)0﹣﹣(﹣1)2013﹣|﹣2|+(﹣)﹣2.
23.计算;(π﹣2)0++(﹣1)2013﹣()﹣2.
24.计算:20130﹣+2cos60°+(﹣2)
25.计算:.
26.计算:2sin30°+(﹣1)2﹣|2﹣|.
实数
一、填空题
1.我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2 i=(﹣1) i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4n i=(i4)n i=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013的值为______.
2.计算:|1﹣|+﹣(3.14﹣π)0﹣(﹣)﹣1=______.
3.计算:
=______.
4.计算:
=______.
5.对于实数a、b,定义运算 如下:a b=,例如,2 4=2﹣4=.计算[2 2]×[(﹣3) 2]=______.
6.计算:
=______.
二、计算题
7.计算:(﹣2)2﹣()0.
8.计算:(1﹣)0﹣+2sin60°﹣|﹣|
9.计算:|﹣|+(2013﹣)0﹣()﹣1﹣2sin60°.
10.计算:
+|﹣3|﹣(π﹣2013)0.
11.计算:.
12.计算:|﹣6|﹣﹣(﹣1)2.
13.计算:.
14.计算:.
15.计算:|﹣3|+.
16.计算:.
17.计算:(﹣1)2013+(2sin30°+)0﹣+()﹣1.
18.计算:(1﹣)0+|﹣|﹣2cos45°+()﹣1.
19.计算:.
20.计算:.
21.计算:.
22.计算:(﹣3)0﹣﹣(﹣1)2013﹣|﹣2|+(﹣)﹣2.
23.计算;(π﹣2)0++(﹣1)2013﹣()﹣2.
24.计算:20130﹣+2cos60°+(﹣2)
25.计算:.
26.计算:2sin30°+(﹣1)2﹣|2﹣|.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
