人教版八年级数学上册同步测试《12.3 角的平分线的性质》(无答案)
文档属性
| 名称 | 人教版八年级数学上册同步测试《12.3 角的平分线的性质》(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 43.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-23 00:00:00 | ||
图片预览

文档简介
《12.3角的平分线的性质》
一、填空题
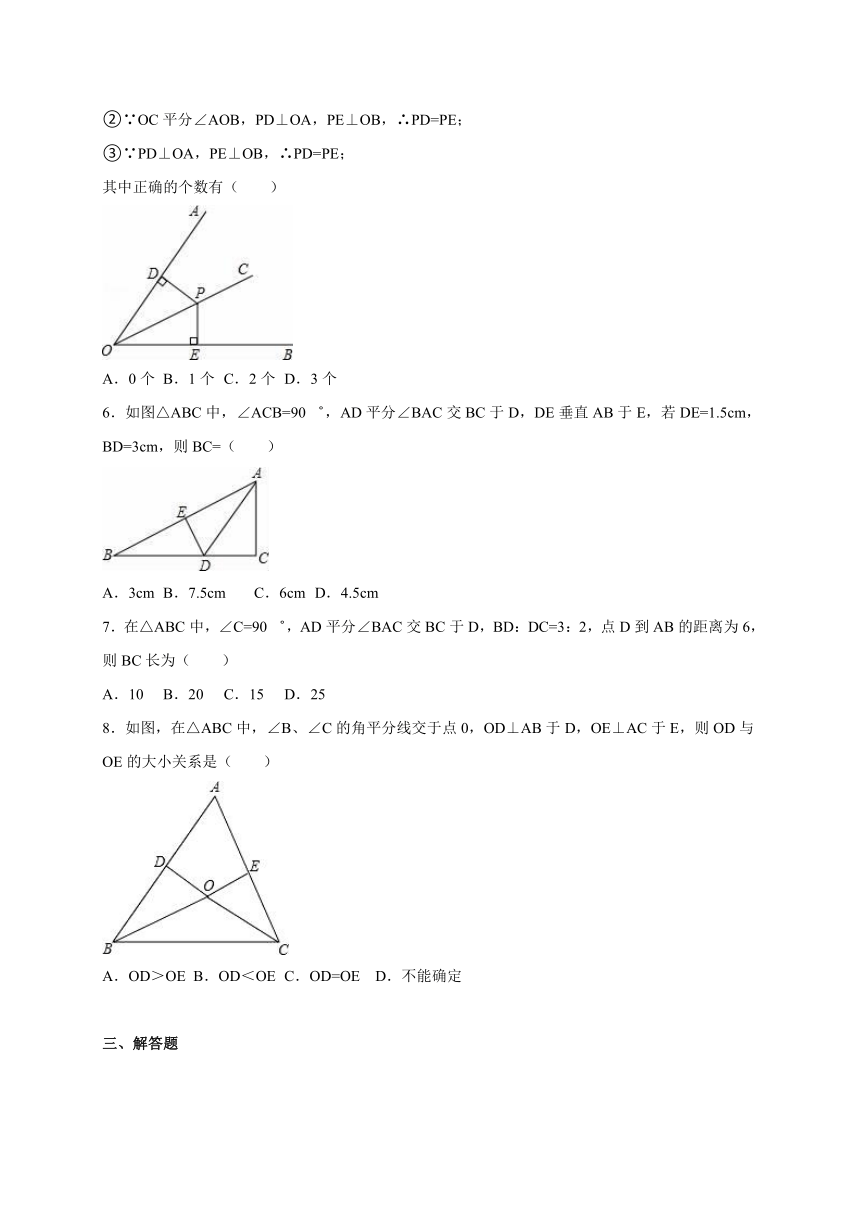
1.如图,∠B=∠D=90゜,根据角平分线性质填空:
(1)若∠1=∠2,则______=______.
(2)若∠3=∠4,则______=______.
2.如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=______.
3.如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则S△ABO:S△BCO:S△CAO等于______.
4.如图,AD是△ABC的角平分线,若AB=2AC.则S△ABD:S△ACD=______.
二、选择题
5.如图,已知点P、D、E分别在OC、OA、OB上,下列推理:
①∵OC平分∠AOB,∴PD=PE;
②∵OC平分∠AOB,PD⊥OA,PE⊥OB,∴PD=PE;
③∵PD⊥OA,PE⊥OB,∴PD=PE;
其中正确的个数有( )
A.0个
B.1个
C.2个
D.3个
6.如图△ABC中,∠ACB=90゜,AD平分∠BAC交BC于D,DE垂直AB于E,若DE=1.5cm,BD=3cm,则BC=( )
A.3cm
B.7.5cm
C.6cm
D.4.5cm
7.在△ABC中,∠C=90゜,AD平分∠BAC交BC于D,BD:DC=3:2,点D到AB的距离为6,则BC长为( )
A.10
B.20
C.15
D.25
8.如图,在△ABC中,∠B、∠C的角平分线交于点0,OD⊥AB于D,OE⊥AC于E,则OD与OE的大小关系是( )
A.OD>OE
B.OD<OE
C.OD=OE
D.不能确定
三、解答题
9.如图,△ABC中,∠C=90゜,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BE=CF,求证:
(1)DE=DC;
(2)BD=DF.
10.如图,四边形ABCD中,AB=AD,CB=CD,点P是AC上一点,PE⊥BC于E,PF⊥CD于F,求证:PE=PF.
11.已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.试说明:PM=PN.
12.如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
13.如图.已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB于R,AB=7,BC=8,AC=9.
(1)求BP、CQ、AR的长.
(2)若BO的延长线交AC于E,CO的延长线交AB于F,若∠A=60゜,求证:OE=OF.
一、填空题
1.如图,∠B=∠D=90゜,根据角平分线性质填空:
(1)若∠1=∠2,则______=______.
(2)若∠3=∠4,则______=______.
2.如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=______.
3.如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则S△ABO:S△BCO:S△CAO等于______.
4.如图,AD是△ABC的角平分线,若AB=2AC.则S△ABD:S△ACD=______.
二、选择题
5.如图,已知点P、D、E分别在OC、OA、OB上,下列推理:
①∵OC平分∠AOB,∴PD=PE;
②∵OC平分∠AOB,PD⊥OA,PE⊥OB,∴PD=PE;
③∵PD⊥OA,PE⊥OB,∴PD=PE;
其中正确的个数有( )
A.0个
B.1个
C.2个
D.3个
6.如图△ABC中,∠ACB=90゜,AD平分∠BAC交BC于D,DE垂直AB于E,若DE=1.5cm,BD=3cm,则BC=( )
A.3cm
B.7.5cm
C.6cm
D.4.5cm
7.在△ABC中,∠C=90゜,AD平分∠BAC交BC于D,BD:DC=3:2,点D到AB的距离为6,则BC长为( )
A.10
B.20
C.15
D.25
8.如图,在△ABC中,∠B、∠C的角平分线交于点0,OD⊥AB于D,OE⊥AC于E,则OD与OE的大小关系是( )
A.OD>OE
B.OD<OE
C.OD=OE
D.不能确定
三、解答题
9.如图,△ABC中,∠C=90゜,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BE=CF,求证:
(1)DE=DC;
(2)BD=DF.
10.如图,四边形ABCD中,AB=AD,CB=CD,点P是AC上一点,PE⊥BC于E,PF⊥CD于F,求证:PE=PF.
11.已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.试说明:PM=PN.
12.如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
13.如图.已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB于R,AB=7,BC=8,AC=9.
(1)求BP、CQ、AR的长.
(2)若BO的延长线交AC于E,CO的延长线交AB于F,若∠A=60゜,求证:OE=OF.
