人教版七年级上册4.2 直线、射线、线段同步练习
文档属性
| 名称 | 人教版七年级上册4.2 直线、射线、线段同步练习 | 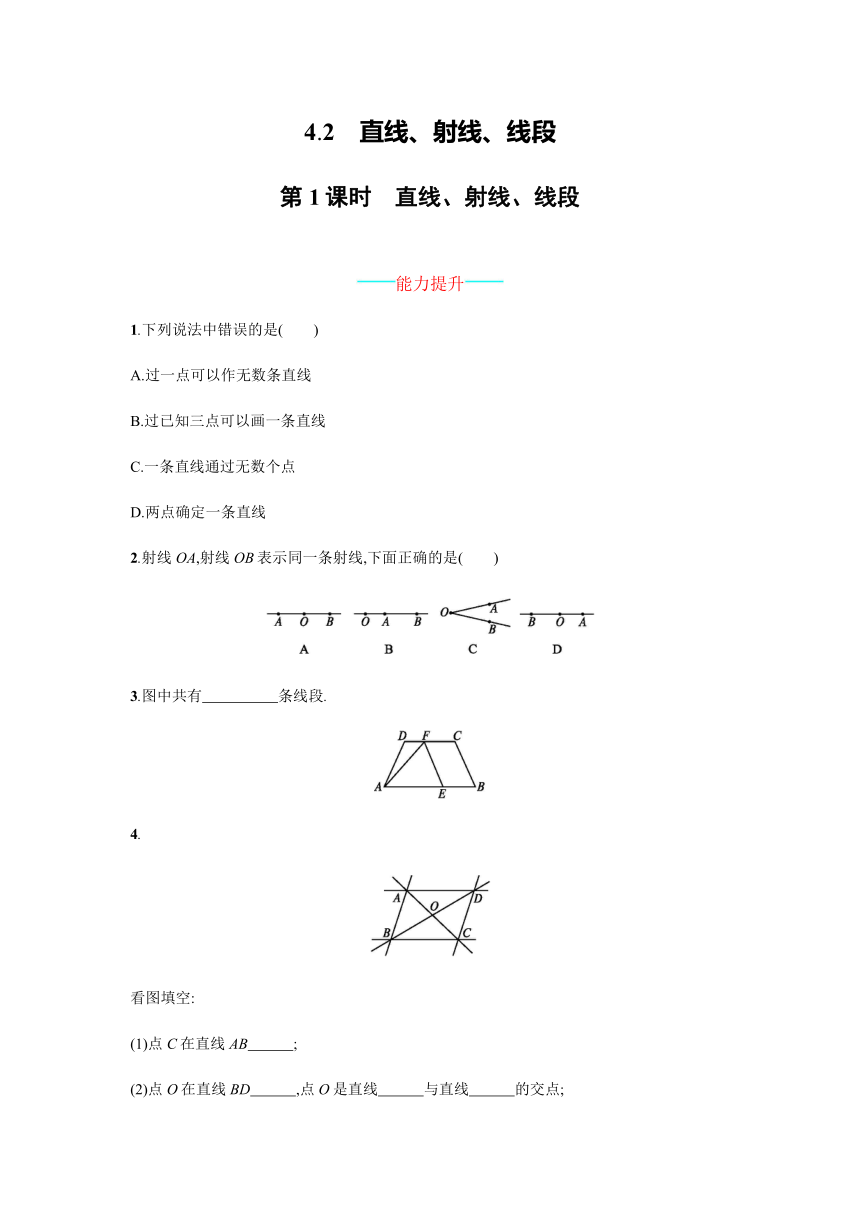 | |
| 格式 | zip | ||
| 文件大小 | 149.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-23 21:03:06 | ||
图片预览





文档简介
4.2 直线、射线、线段
第1课时 直线、射线、线段
能力提升
1.下列说法中错误的是( )
A.过一点可以作无数条直线
B.过已知三点可以画一条直线
C.一条直线通过无数个点
D.两点确定一条直线
2.射线OA,射线OB表示同一条射线,下面正确的是( )
3.图中共有 条线段.
4.
看图填空:
(1)点C在直线AB ;
(2)点O在直线BD ,点O是直线 与直线 的交点;
(3)过点A的直线共有 条,它们是 .
5.
如图所示,在线段AB上任取D,E,C三个点,则这个图中共有 条线段.
6.木工检验木条的边线是否是直的,常常用眼睛从木条的一端向另一端望去,如果看到两个端点及这条边线中的各点都重合于一点,那么这条边线就是直的,你可以同伙伴试一试这种方法,并说一说其中的道理.
7.按下列语句画出图形.
(1)直线l经过A,B,C三点,点C在点A与点B之间;
(2)经过点O的三条直线a,b,c;
(3)两条直线AB与CD相交于点P;
(4)P是直线a外一点,经过点P有一条直线b与直线a相交于点Q.
★8.阅读下表:
线段AB上的点数n(包括A,B两点)
图例
线段总条数N
3
3=2+1
4
6=3+2+1
5
10=4+3+2+1
6
15=5+4+3+2+1
解答下列问题:
(1)根据表中规律猜测线段总数N与线段上的点数n(包括线段两个端点)有什么关系
(2)根据上述关系解决如下实际问题:有一辆客车往返于A,B两地,中途停靠三个站点,如果任意两站间的票价都不同,问:①有多少种不同的票价 ②要准备多少种车票
创新应用
★9.
如图,l1与l2是同一平面内的两条相交直线,它们有一个交点.如果在这个平面内再画第三条直线l3,那么这3条直线最多可有 个交点;如果在这个平面内再画第4条直线l4,那么这4条直线最多可有 个交点.由此,我们可以猜想:在同一平面内,n(n为大于1的整数)条直线最多可有 个交点.(用含n的式子表示)
参考答案
能力提升
1.B 过三点画直线,要看这三点在不在一条直线上,若不在,则无法画出.
2.B 射线自端点向一方无限延伸,因为表示射线时字母有顺序性,即端点字母写在前面,所以点A、点B应在点O的同侧且三点在同一条直线上.
3.10
4.(1)外 (2)上 AC BD (3)3 直线AD、直线AB、直线AC 这类题,必须认真观察图形,弄清各元素的位置关系,用精练、准确的语言表达.
5.10 只要有一个端点不相同,就是不同的线段.
6.解:经过两点有且只有一条直线.
7.解:(1)
(2)
(3)
(4)
8.解:(1)N=1+2+3+…+(n-1)=.
(2)①A,B两地之间有三个站点,说明在这条线段上有5个点,则共有=10条线段,即有10种票价;②由于从A到B和从B到A的车票不同,则要准备10×2=20种车票.
创新应用
9.3 6 通过作图发现:3条直线最多有交点1+2=3(个);4条直线最多有交点1+2+3=6(个);5条直线最多有交点1+2+3+4=10(个)……n条直线最多有交点1+2+3+…+(n-1)=(个).
第2课时 线段的性质
能力提升
1.如图所示,要在直线PQ上找一点C,使PC=3CQ,则点C应在( )
A.P,Q之间
B.点P的左边
C.点Q的右边
D.P,Q之间或在点Q的右边
2.如果线段AB=5
cm,BC=3
cm,那么A,C两点间的距离是( )
A.8
cm
B.2
cm
C.4
cm
D.不能确定
3.C为线段AB的一个三等分点,D为线段AB的中点,若AB的长为6.6
cm,则CD的长为( )
A.0.8
cm
B.1.1
cm
C.3.3
cm
D.4.4
cm
4.如图所示,C是线段AB的中点,D是CB上一点,下列说法中错误的是( )
A.CD=AC-BD
B.CD=BC
C.CD=AB-BD
D.CD=AD-BC
5.下面给出的4条线段中,最长的是( )
A.d
B.c
C.b
D.a
6.已知A,B是数轴上的两点,点A表示的数是-1,且线段AB的长度为6,则点B表示的数是 .
7.已知线段AB=7
cm,在线段AB所在的直线上画线段BC=1
cm,则线段AC= .
8.
如图所示,设A,B,C,D为4个居民小区,现要在四边形ABCD内建一个购物中心,试问把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小 请说明理由.
9.
如图所示,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点.
(1)如果AB=20
cm,AM=6
cm,求NC的长;
(2)如果MN=6
cm,求AB的长.
10.在桌面上放了一个正方体的盒子,如图所示,一只蚂蚁在顶点A处,它要爬到顶点B处找食物,你能帮助蚂蚁设计一条最短的爬行路线吗 要是食物在顶点C处呢
★11.已知线段AB=12
cm,直线AB上有一点C,且BC=6
cm,M是线段AC的中点,求线段AM的长.
创新应用
★12.在同一条公路旁,住着5人,他们在同一家公司上班,如图,不妨设这5人的家分别住在点A,B,D,E,F所示的位置,公司在点C处,若AB=4
km,BC=2
km,CD=3
km,DE=3
km,EF=1
km,他们全部乘出租车上班,车费单位报销.出租车收费标准是:起步价6元(3
km以内,包括3
km),超过3
km超出的部分每千米1.5元(不足1
km,以1
km计算),每辆车能容纳3人.
(1)若他们分别乘出租车去上班,公司应支付车费多少元
(2)如果你是公司经理,你对他们有没有什么建议
参考答案
能力提升
1.D 注意本题中的条件是在直线PQ上找一点C,所以C可以在P,Q之间,也可以在点Q的右侧.
2.D A,B,C三点位置不确定,可能共线,也可能不共线.
3.B
如图,AD=AB=3.3cm,AC=AB=2.2cm,
所以CD=AD-AC=3.3-2.2=1.1(cm).
4.B 5.A
6.-7或5 点B可能在点A的左侧,也有可能在点A的右侧.若点B在点A的左侧,则点B表示的数比点A表示的数小6,此时点B表示的数为-7;若点B在点A的右侧,则点B表示的数比点A表示的数大6,此时点B表示的数为5.
7.8
cm或6
cm 分两种情况:①点C在线段AB内,②点C在线段AB的延长线上.
8.
解:连接AC,BD,交点P即为购物中心的位置.
理由:根据公理“两点之间,线段最短”,要使购物中心到A,B,C,D的距离和最小,购物中心既要在AC上,又要在BD上.
9.解:(1)因为M为AC的中点,
所以MC=AM.
又因为AM=6cm,
所以AC=2×6=12(cm).
因为AB=20cm,
所以BC=AB-AC=20-12=8(cm).
又因为N为BC的中点,
所以NC=BC=4(cm).
(2)因为M为AC的中点,所以MC=AM.
因为N为BC的中点,所以CN=BN.
所以AB=AC+BC=2(MC+CN)=2MN=2×6=12(cm).
10.解:如图所示,是该正方体的侧面展开图.食物在B处时的最短路线为线段AB,食物在C处时的最短路线为线段AC.
11.解:(1)当点C在线段AB上时,如图①,
图①
因为M是AC的中点,
所以AM=AC.
又因为AC=AB-BC,AB=12cm,BC=6cm,
所以AM=(AB-BC)=×(12-6)=3(cm).
(2)当点C在线段AB的延长线上时,如图②,
图②
因为M是AC的中点,
所以AM=AC.
又因为AC=AB+BC,AB=12cm,BC=6cm,
所以AM=AC=(AB+BC)=×(12+6)=9(cm).故AM的长度为3cm或9cm.
创新应用
12.解:(1)在A处乘车的车费为6+(4+2-3)×1.5=10.5(元);
在B处乘车的车费为6元;
在D处乘车的车费为6元;
在E处乘车的车费为6+(3+3-3)×1.5=10.5(元);
在F处乘车的车费为6+(1+3+3-3)×1.5=12(元),合计45元.
(2)A,B同乘一辆车,从A开出,D,E,F同乘一辆车,从F开出,合计22.5元.
第1课时 直线、射线、线段
能力提升
1.下列说法中错误的是( )
A.过一点可以作无数条直线
B.过已知三点可以画一条直线
C.一条直线通过无数个点
D.两点确定一条直线
2.射线OA,射线OB表示同一条射线,下面正确的是( )
3.图中共有 条线段.
4.
看图填空:
(1)点C在直线AB ;
(2)点O在直线BD ,点O是直线 与直线 的交点;
(3)过点A的直线共有 条,它们是 .
5.
如图所示,在线段AB上任取D,E,C三个点,则这个图中共有 条线段.
6.木工检验木条的边线是否是直的,常常用眼睛从木条的一端向另一端望去,如果看到两个端点及这条边线中的各点都重合于一点,那么这条边线就是直的,你可以同伙伴试一试这种方法,并说一说其中的道理.
7.按下列语句画出图形.
(1)直线l经过A,B,C三点,点C在点A与点B之间;
(2)经过点O的三条直线a,b,c;
(3)两条直线AB与CD相交于点P;
(4)P是直线a外一点,经过点P有一条直线b与直线a相交于点Q.
★8.阅读下表:
线段AB上的点数n(包括A,B两点)
图例
线段总条数N
3
3=2+1
4
6=3+2+1
5
10=4+3+2+1
6
15=5+4+3+2+1
解答下列问题:
(1)根据表中规律猜测线段总数N与线段上的点数n(包括线段两个端点)有什么关系
(2)根据上述关系解决如下实际问题:有一辆客车往返于A,B两地,中途停靠三个站点,如果任意两站间的票价都不同,问:①有多少种不同的票价 ②要准备多少种车票
创新应用
★9.
如图,l1与l2是同一平面内的两条相交直线,它们有一个交点.如果在这个平面内再画第三条直线l3,那么这3条直线最多可有 个交点;如果在这个平面内再画第4条直线l4,那么这4条直线最多可有 个交点.由此,我们可以猜想:在同一平面内,n(n为大于1的整数)条直线最多可有 个交点.(用含n的式子表示)
参考答案
能力提升
1.B 过三点画直线,要看这三点在不在一条直线上,若不在,则无法画出.
2.B 射线自端点向一方无限延伸,因为表示射线时字母有顺序性,即端点字母写在前面,所以点A、点B应在点O的同侧且三点在同一条直线上.
3.10
4.(1)外 (2)上 AC BD (3)3 直线AD、直线AB、直线AC 这类题,必须认真观察图形,弄清各元素的位置关系,用精练、准确的语言表达.
5.10 只要有一个端点不相同,就是不同的线段.
6.解:经过两点有且只有一条直线.
7.解:(1)
(2)
(3)
(4)
8.解:(1)N=1+2+3+…+(n-1)=.
(2)①A,B两地之间有三个站点,说明在这条线段上有5个点,则共有=10条线段,即有10种票价;②由于从A到B和从B到A的车票不同,则要准备10×2=20种车票.
创新应用
9.3 6 通过作图发现:3条直线最多有交点1+2=3(个);4条直线最多有交点1+2+3=6(个);5条直线最多有交点1+2+3+4=10(个)……n条直线最多有交点1+2+3+…+(n-1)=(个).
第2课时 线段的性质
能力提升
1.如图所示,要在直线PQ上找一点C,使PC=3CQ,则点C应在( )
A.P,Q之间
B.点P的左边
C.点Q的右边
D.P,Q之间或在点Q的右边
2.如果线段AB=5
cm,BC=3
cm,那么A,C两点间的距离是( )
A.8
cm
B.2
cm
C.4
cm
D.不能确定
3.C为线段AB的一个三等分点,D为线段AB的中点,若AB的长为6.6
cm,则CD的长为( )
A.0.8
cm
B.1.1
cm
C.3.3
cm
D.4.4
cm
4.如图所示,C是线段AB的中点,D是CB上一点,下列说法中错误的是( )
A.CD=AC-BD
B.CD=BC
C.CD=AB-BD
D.CD=AD-BC
5.下面给出的4条线段中,最长的是( )
A.d
B.c
C.b
D.a
6.已知A,B是数轴上的两点,点A表示的数是-1,且线段AB的长度为6,则点B表示的数是 .
7.已知线段AB=7
cm,在线段AB所在的直线上画线段BC=1
cm,则线段AC= .
8.
如图所示,设A,B,C,D为4个居民小区,现要在四边形ABCD内建一个购物中心,试问把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小 请说明理由.
9.
如图所示,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点.
(1)如果AB=20
cm,AM=6
cm,求NC的长;
(2)如果MN=6
cm,求AB的长.
10.在桌面上放了一个正方体的盒子,如图所示,一只蚂蚁在顶点A处,它要爬到顶点B处找食物,你能帮助蚂蚁设计一条最短的爬行路线吗 要是食物在顶点C处呢
★11.已知线段AB=12
cm,直线AB上有一点C,且BC=6
cm,M是线段AC的中点,求线段AM的长.
创新应用
★12.在同一条公路旁,住着5人,他们在同一家公司上班,如图,不妨设这5人的家分别住在点A,B,D,E,F所示的位置,公司在点C处,若AB=4
km,BC=2
km,CD=3
km,DE=3
km,EF=1
km,他们全部乘出租车上班,车费单位报销.出租车收费标准是:起步价6元(3
km以内,包括3
km),超过3
km超出的部分每千米1.5元(不足1
km,以1
km计算),每辆车能容纳3人.
(1)若他们分别乘出租车去上班,公司应支付车费多少元
(2)如果你是公司经理,你对他们有没有什么建议
参考答案
能力提升
1.D 注意本题中的条件是在直线PQ上找一点C,所以C可以在P,Q之间,也可以在点Q的右侧.
2.D A,B,C三点位置不确定,可能共线,也可能不共线.
3.B
如图,AD=AB=3.3cm,AC=AB=2.2cm,
所以CD=AD-AC=3.3-2.2=1.1(cm).
4.B 5.A
6.-7或5 点B可能在点A的左侧,也有可能在点A的右侧.若点B在点A的左侧,则点B表示的数比点A表示的数小6,此时点B表示的数为-7;若点B在点A的右侧,则点B表示的数比点A表示的数大6,此时点B表示的数为5.
7.8
cm或6
cm 分两种情况:①点C在线段AB内,②点C在线段AB的延长线上.
8.
解:连接AC,BD,交点P即为购物中心的位置.
理由:根据公理“两点之间,线段最短”,要使购物中心到A,B,C,D的距离和最小,购物中心既要在AC上,又要在BD上.
9.解:(1)因为M为AC的中点,
所以MC=AM.
又因为AM=6cm,
所以AC=2×6=12(cm).
因为AB=20cm,
所以BC=AB-AC=20-12=8(cm).
又因为N为BC的中点,
所以NC=BC=4(cm).
(2)因为M为AC的中点,所以MC=AM.
因为N为BC的中点,所以CN=BN.
所以AB=AC+BC=2(MC+CN)=2MN=2×6=12(cm).
10.解:如图所示,是该正方体的侧面展开图.食物在B处时的最短路线为线段AB,食物在C处时的最短路线为线段AC.
11.解:(1)当点C在线段AB上时,如图①,
图①
因为M是AC的中点,
所以AM=AC.
又因为AC=AB-BC,AB=12cm,BC=6cm,
所以AM=(AB-BC)=×(12-6)=3(cm).
(2)当点C在线段AB的延长线上时,如图②,
图②
因为M是AC的中点,
所以AM=AC.
又因为AC=AB+BC,AB=12cm,BC=6cm,
所以AM=AC=(AB+BC)=×(12+6)=9(cm).故AM的长度为3cm或9cm.
创新应用
12.解:(1)在A处乘车的车费为6+(4+2-3)×1.5=10.5(元);
在B处乘车的车费为6元;
在D处乘车的车费为6元;
在E处乘车的车费为6+(3+3-3)×1.5=10.5(元);
在F处乘车的车费为6+(1+3+3-3)×1.5=12(元),合计45元.
(2)A,B同乘一辆车,从A开出,D,E,F同乘一辆车,从F开出,合计22.5元.
