4.1.1立体图形与平面图形同步练习
文档属性
| 名称 | 4.1.1立体图形与平面图形同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 306.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-25 15:17:30 | ||
图片预览


文档简介
第四章 几何图形初步
4.1 几何图形
4.1.1 立体图形与平面图形
第1课时 几何图形
能力提升
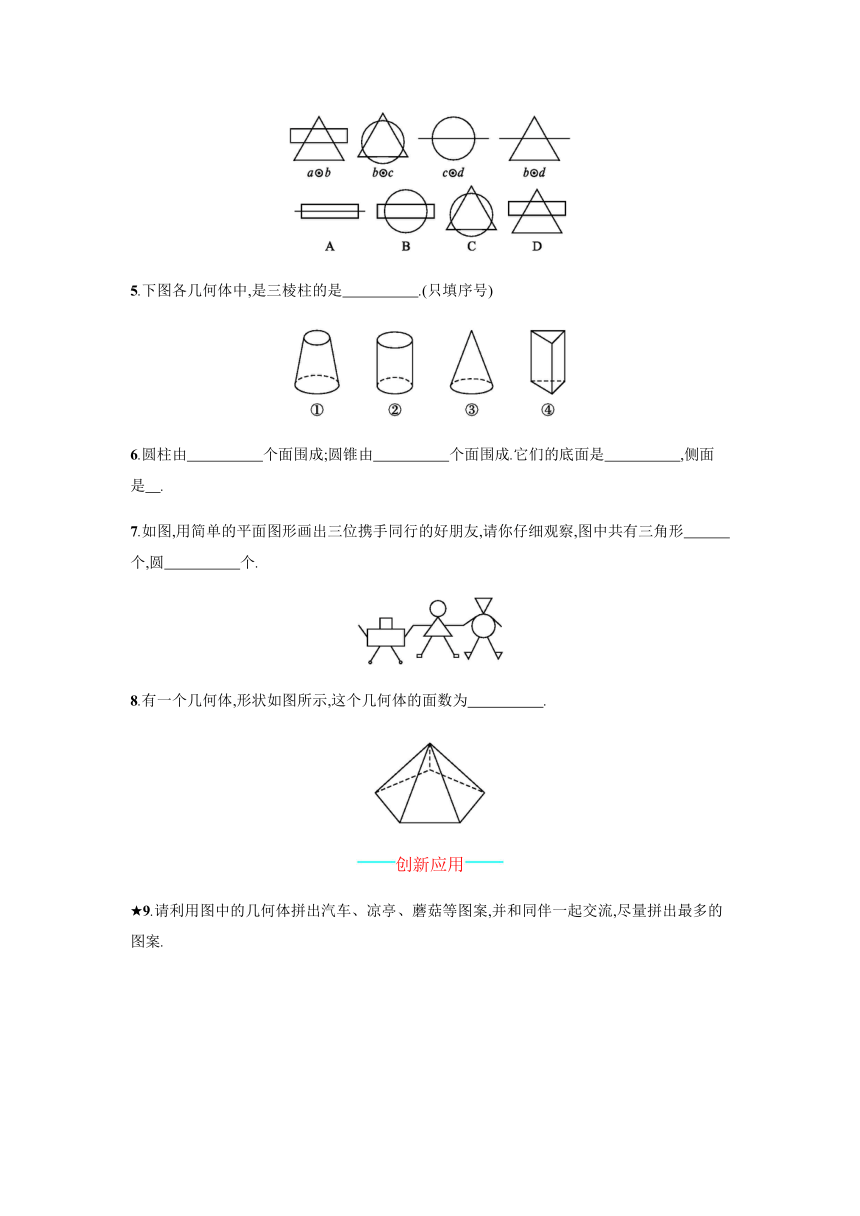
1.下列所列举的物体,与圆锥的形状类似的是( )
A.足球
B.字典
C.易拉罐
D.标枪的尖头
2.下列图形属于柱体的是( )
3.在如图所示的几何体中,由四个面围成的几何体是
( )
4.下列第一行所示的四个图形,每个图形均是由四种简单的图形a,b,c,d(圆、直线、三角形、长方形)中的两种组成.例如由a,b组成的图形记作a☉b,那么由此可知,下面第二行的图中可以记作a☉d的是
( )
5.下图各几何体中,是三棱柱的是 .(只填序号)
6.圆柱由 个面围成;圆锥由 个面围成.它们的底面是 ,侧面是 .
7.如图,用简单的平面图形画出三位携手同行的好朋友,请你仔细观察,图中共有三角形 个,圆 个.
8.有一个几何体,形状如图所示,这个几何体的面数为 .
创新应用
★9.请利用图中的几何体拼出汽车、凉亭、蘑菇等图案,并和同伴一起交流,尽量拼出最多的图案.
参考答案
能力提升
1.D 2.C
3.C A有五个面;B有三个面;C有四个面;D有三个面,故选C.
4.A 根据题意,知a代表长方形,d代表直线,所以记作a☉d的图形是长方形和直线的组合,故选A.
5.④
6.3 2 平面 曲面
7.4 4
8.6
创新应用
9.分析:本题是开放性试题,只要所给答案合理即可.
解:答案不唯一,如图.
第2课时 几何图形的三种形状图与展开图
能力提升
1.下列四个图中,是三棱锥的表面展开图的是( )
2.下列图形经过折叠,能围成圆锥的是( )
3.
将右面正方体的平面展开图重新折成正方体后,“共”字对面的字是( )
A.阖
B.家
C.幸
D.福
4.骰子是一种特殊的数字立方体(如图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
5.下图是从不同方向看某一几何体得到的平面图形,则这个几何体是 .
6.根据下列多面体的平面展开图,填写多面体的名称:
(1) ,(2) ,(3) .
7.将下图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去 .(填序号)
8.
如图,画出所给几何体的从正面看、左面看和上面看得到的图形.
创新应用
★9.如图是火箭腾空的立体图形(火箭圆柱底面的周长不等于圆柱的高),请你画出火箭的平面展开图.
★10.如图,水平放置的长方体的底面是边长为2和4的长方形,从左边看该长方体,得到的图形的面积是6,试求该长方体的体积.
参考答案
能力提升
1.B 三棱锥的四个面都是三角形,还要能围成一个立体图形,可排除C,D;而A不能围成立体图形,故选B.
2.B 3.C
4.C 根据题意,骰子的平面展开图共有六个面,其中面“1”与面“6”相对,面“4”与面“3”相对,面“2”与面“5”相对.所以只有C中的相对两个面上的点数与立体图形一致.
5.圆柱
6.(1)长方体 (2)三棱柱 (3)三棱锥
7.1或2或6
8.解:
创新应用
9.解:
10.解:由题意知长方体的高为3,则体积为4×2×3=24.
4.1 几何图形
4.1.1 立体图形与平面图形
第1课时 几何图形
能力提升
1.下列所列举的物体,与圆锥的形状类似的是( )
A.足球
B.字典
C.易拉罐
D.标枪的尖头
2.下列图形属于柱体的是( )
3.在如图所示的几何体中,由四个面围成的几何体是
( )
4.下列第一行所示的四个图形,每个图形均是由四种简单的图形a,b,c,d(圆、直线、三角形、长方形)中的两种组成.例如由a,b组成的图形记作a☉b,那么由此可知,下面第二行的图中可以记作a☉d的是
( )
5.下图各几何体中,是三棱柱的是 .(只填序号)
6.圆柱由 个面围成;圆锥由 个面围成.它们的底面是 ,侧面是 .
7.如图,用简单的平面图形画出三位携手同行的好朋友,请你仔细观察,图中共有三角形 个,圆 个.
8.有一个几何体,形状如图所示,这个几何体的面数为 .
创新应用
★9.请利用图中的几何体拼出汽车、凉亭、蘑菇等图案,并和同伴一起交流,尽量拼出最多的图案.
参考答案
能力提升
1.D 2.C
3.C A有五个面;B有三个面;C有四个面;D有三个面,故选C.
4.A 根据题意,知a代表长方形,d代表直线,所以记作a☉d的图形是长方形和直线的组合,故选A.
5.④
6.3 2 平面 曲面
7.4 4
8.6
创新应用
9.分析:本题是开放性试题,只要所给答案合理即可.
解:答案不唯一,如图.
第2课时 几何图形的三种形状图与展开图
能力提升
1.下列四个图中,是三棱锥的表面展开图的是( )
2.下列图形经过折叠,能围成圆锥的是( )
3.
将右面正方体的平面展开图重新折成正方体后,“共”字对面的字是( )
A.阖
B.家
C.幸
D.福
4.骰子是一种特殊的数字立方体(如图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
5.下图是从不同方向看某一几何体得到的平面图形,则这个几何体是 .
6.根据下列多面体的平面展开图,填写多面体的名称:
(1) ,(2) ,(3) .
7.将下图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去 .(填序号)
8.
如图,画出所给几何体的从正面看、左面看和上面看得到的图形.
创新应用
★9.如图是火箭腾空的立体图形(火箭圆柱底面的周长不等于圆柱的高),请你画出火箭的平面展开图.
★10.如图,水平放置的长方体的底面是边长为2和4的长方形,从左边看该长方体,得到的图形的面积是6,试求该长方体的体积.
参考答案
能力提升
1.B 三棱锥的四个面都是三角形,还要能围成一个立体图形,可排除C,D;而A不能围成立体图形,故选B.
2.B 3.C
4.C 根据题意,骰子的平面展开图共有六个面,其中面“1”与面“6”相对,面“4”与面“3”相对,面“2”与面“5”相对.所以只有C中的相对两个面上的点数与立体图形一致.
5.圆柱
6.(1)长方体 (2)三棱柱 (3)三棱锥
7.1或2或6
8.解:
创新应用
9.解:
10.解:由题意知长方体的高为3,则体积为4×2×3=24.
