四川省2017高考数学复习备考:考纲分析+考题研究+备考策略(共100张PPT)
文档属性
| 名称 | 四川省2017高考数学复习备考:考纲分析+考题研究+备考策略(共100张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-25 21:36:31 | ||
图片预览







文档简介
课件100张PPT。发挥集体智慧
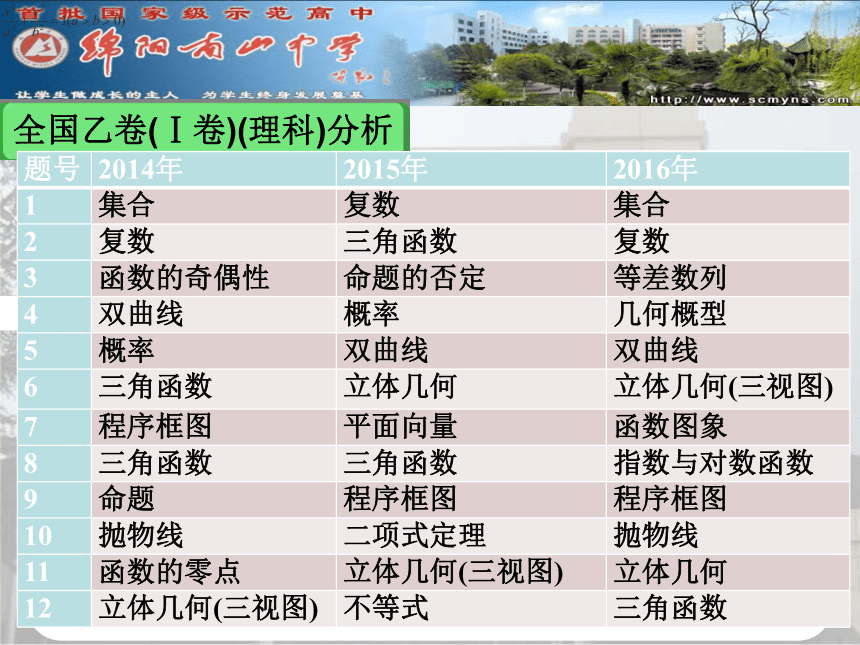
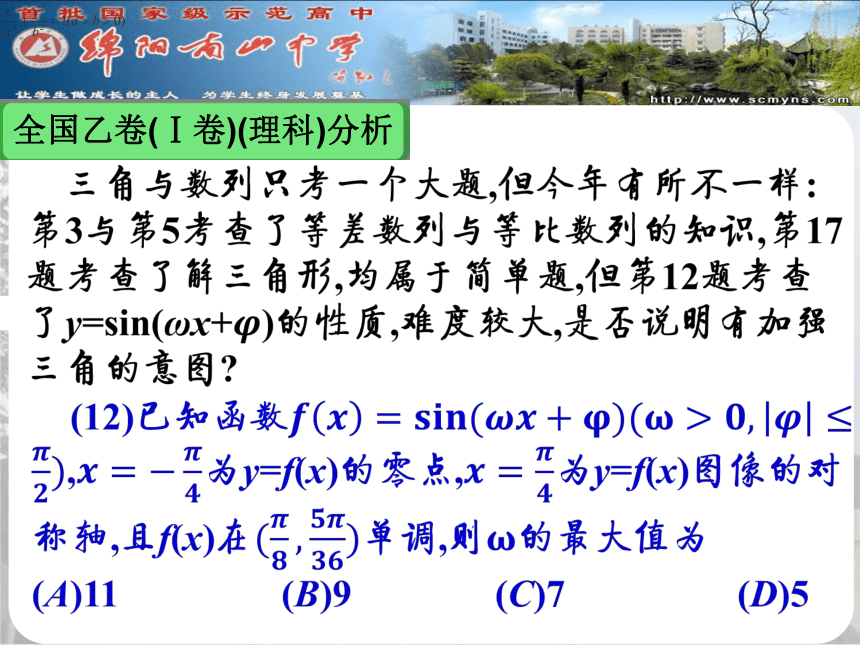
创建高效团队全国乙卷(Ⅰ卷)(理科)分析全国乙卷(Ⅰ卷)(理科)分析全国乙卷(Ⅰ卷)(理科)分析新增的不同于往年的考点:
第4题考查平时关注较少的几何概型:?全国乙卷(Ⅰ卷)(理科)分析第16题考查了应用型的线性规划:
某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为 元.
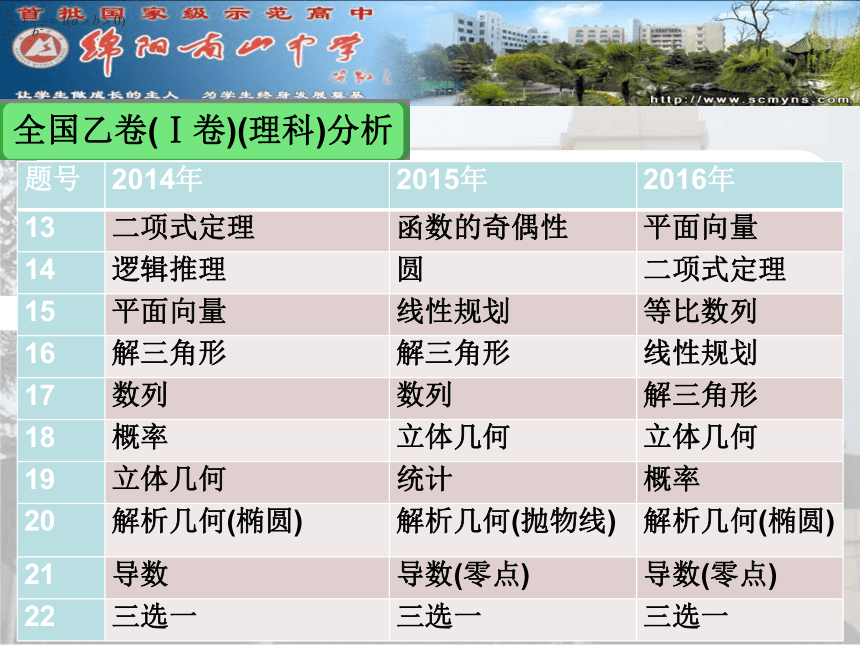
全国乙卷(Ⅰ卷)(理科)分析??全国乙卷(Ⅰ卷)(理科)分析二.立足基础,梯度合理
选择题前6个,属于简单试题,后面4个属于中档试题,最后两个难度较大,填空题前三个是简单题,最后一个需要很强的阅读提取信息的能力、建模和准确作图的能力,属于难题.
只要学生基石功扎实,17,18,19,20题第一问是较简单的基础题,20题第2问与21题有一定的难度,有较好的区分度.全国乙卷(Ⅰ卷)(理科)分析三.能力立意,适度创新
今年的试卷.对很多都要求学生有很好的思维能力,特别是创新意识的考查有所增加.
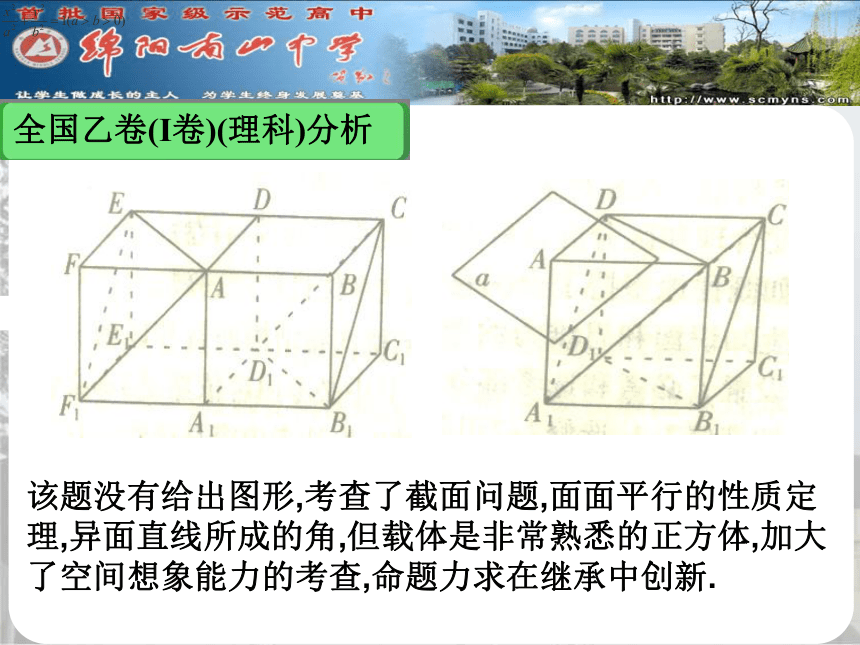
如第11题:?全国乙卷(Ⅰ卷)(理科)分析该题没有给出图形,考查了截面问题,面面平行的性质定理,异面直线所成的角,但载体是非常熟悉的正方体,加大了空间想象能力的考查,命题力求在继承中创新.全国乙卷(Ⅰ卷)(理科)分析 第4题与必修13第136页例1很相似,第16题线性规划与必修1第87页的引例如出一辙,是一个整点问题.
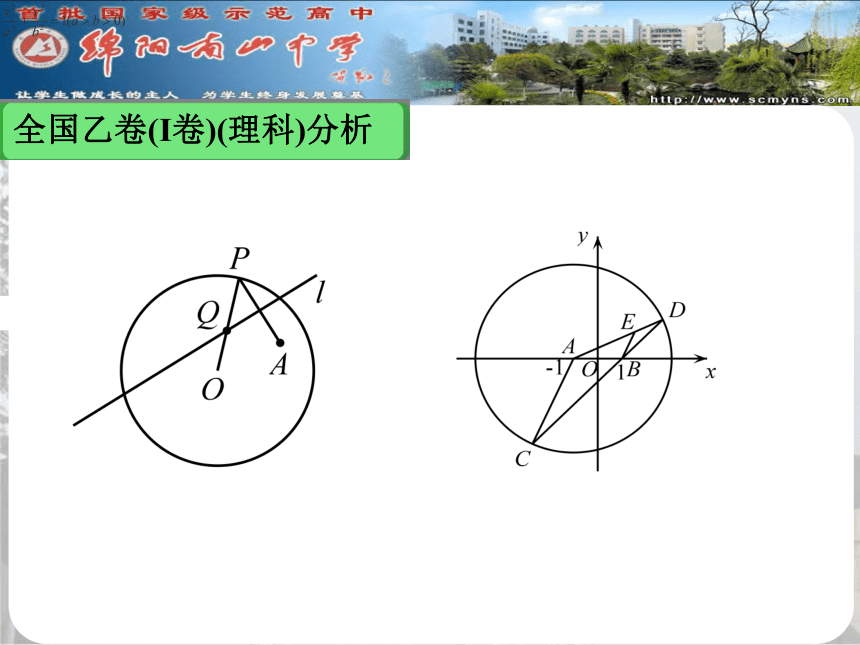
课本选修2-1第49页的习题:
圆O的半径为r,A是圆内一定点,P是圆上一动点,线段PA的垂直平分线与PO交于点Q,当点P在圆上运动时,点Q的轨迹是什么?为什么?全国乙卷(Ⅰ卷)(理科)分析?全国乙卷(Ⅰ卷)(理科)分析全国乙卷(Ⅰ卷)(理科)分析五.突出思想,注重通法
(3)已知等差数列{an}前9项的和为27,a10=8,则a100=
(A)100 (B)99 (C)98 (D)97?全国甲卷(Ⅱ卷理科)分析全国甲卷(Ⅱ卷)分析1.注意基础,平实近人
选择题前9个,填空题前3个与解答题前三个与选做题都是由基本知识、基本方法和常见材料构成.
2.立德树人,贴近实际
理科(5)
如图,小明从街道的E处出发,
先到F处与小红会合,再一起到
位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )
(A)24 (B)18 (C) 12 (D)9
全国甲卷(Ⅱ卷)分析?全国甲卷(Ⅱ卷)分析理科(8)与文科(9)
中国古代有计算多项式值的
秦九韶算法,下图是实现该算法
的程序框图.执行该程序框图,
若输入的x=2,n=2,依次输入的
为2,2,5,则输出的 ( )
(A)7 (B)12 (C)17 (D)34全国甲卷(Ⅱ卷)分析文科(18) 某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
(Ⅰ)记A为事件:“一续保人本年度的保费不高于基本保费”.求P(A)的估计值;
(Ⅱ)记B为事件:“一续保人本年 度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;
(Ⅲ)求续保人本年度的平均保费估计值.
全国甲卷(Ⅱ卷)分析3.体现差异,文理联姻
相对简单的题,全卷有6个题是相同的试题,相对较难的试题往往成为血缘题或姐妹题,全卷不同的题有13道.
4.依据课标,重视教材
引导我们要重视教材的学习,而不是考什么才学什么,而是学了什么才考什么,学了不一定考,不学也可能考,考的一定是学过的,不考的也可能是要求学的.让学生多一些知识的积累,多一些视野,多一些思考,多一些智慧和力量.全国甲卷(Ⅱ卷)分析 课标中要求:通过阅读中国古代数学中的算法案例,体会中国古代数学对世界数学发展的贡献.今年文科与理科都考查了秦九韶算法.
课标中说:了解随机数的意义,能运用模拟方法(包括计算器产生随机数来进行模拟)估计概率,初步体会几何概型的意义.教材中也有利用这种方法计算圆周率的例题.这要求教师改变教学方式,落实课标要求,回归教材,规避教辅资料.全国甲卷(Ⅱ卷)分析?全国甲卷(Ⅱ卷)分析5.回避套路,强调能力
一类题没在公理、没有原理、没有运算、没有成熟的解题套路,需要的是学生的逻辑推理能力.这种通过所学基础知识,获得解决问题的方法并能运用之解决生活实际中遇到的问题,正是我们希望学生所具有的能力.全国甲卷(Ⅱ卷)分析文科(16)与理科(15)
有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是 .全国甲卷(Ⅱ卷)分析2014年全国Ⅰ卷,文科与理科14题:
甲、乙、丙三位同学被问到是否去过A,B,C三个城市时,
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市;
丙说:我们三人去过同一个城市.
由此可判断乙去过的城市为 .全国甲卷(Ⅱ卷)分析6.易题求新,难题重质
17.(理科)
Sn为等差数列{an}的前n项和,且a1=1,S7=28,记bn=[lgan],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg99]=1.
(Ⅰ)求b1,b11,b101;
(Ⅱ)求数列{bn}的前1 000项和.全国甲卷(Ⅱ卷)分析17.(文科)
等差数列{an}中,a3+a4=4,a5+a7=6.
(Ⅰ)求{an}的通项公式;
(Ⅱ) 设bn=[an],求数列{bn}的前10项和,其中[x]表示不超过x的最大整数,如[0.9]=0,[2.6]=2.这本是两个难度较小的试题,但在学生熟悉的数列中巧妙地引入高斯函数,突然使此题摆脱了平庸.全国甲卷(Ⅱ卷)分析全国甲卷(Ⅱ卷)分析7.注意素养,考查思想
全卷注重对数学核心素养的考查,除对数学抽象、逻辑推理、直观想象、数学运算、数据分析、数学建模等六个核心素养的考查外,特别对数学思想与方法进行了考查.如:全国甲卷(Ⅱ卷)分析?解答 由f(-x)=2-f(x)马上构造一个函数f(x)=x+1即可.
这是典型的特殊与一般的思想的应用.若数形结合能力好的学生立即可得到函数f(x)关于点(0,1)对称.全国甲卷(Ⅱ卷)分析?全国甲卷(Ⅱ卷)分析理科20与文科21题第一问,利用数形结合很容易看到AM与AN的对称性,从而问题很好解决.全国甲卷(Ⅱ卷)分析备课组的一些做法一.加强集合备课,任务分工明确.备课组的一些做法一.加强集合备课,任务分工明确.备课组的一些做法一.加强集合备课,任务分工明确.备课组的一些做法一.加强集合备课,任务分工明确.南山中学2017级高三
数学纠错卡备课组的一些做法二. 集体备课模式(以数列为例)一.考纲要求
1.了解数列的概念与几种表示法
2.理解、掌握等差、等比数列的概念通项公式与前n项和公式
3.能在具体的情境中识别数列的等差关系或等比关系
4.能用等差、等比数列的相关知识解决相应的实际问题
5.了解等差数列与一次函数的关系、等比数列的指数函数的关系2. 集体备课的模式(以数列为例)备课组的一些做法备课组的一些做法二. 集体备课模式(以数列为例)3.知识网络备课组的一些做法4. 全国卷近年考题类型?备课组的一些做法?4. 全国卷近年考题类型备课组的一些做法二.等差数列、等比数列的相关公式及其性质的考查
例5 (2016年全国Ⅱ卷,理科17题)Sn为等差数列{an}的前n项和,且a1=1,S7=28,记bn=[lgan],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg99]=1.
(Ⅰ)求b1,b11,b101;
(Ⅱ)求数列{bn}的前1 000项和.
例6 (2016年全国Ⅱ卷,文科第17题)等差数列{an}中,a3+a4=4,a5+a7=6.
(Ⅰ)求{an}的通项公式;
(Ⅱ) 设bn=[an],求数列{bn}的前10项和,其中[x]表示不超过x的最大整数,如[0.9]=0,[2.6]=2.4. 全国卷近年考题类型备课组的一些做法三.运用累差叠加法、错位相减法、裂项法求和4. 全国卷近年考题类型备课组的一些做法三.运用累差叠加法、错位相减法、裂项法求和4. 全国卷近年考题类型备课组的一些做法四.Sn与an关系的运用4. 全国卷近年考题类型备课组的一些做法四.Sn与an关系的运用4. 全国卷近年考题类型备课组的一些做法五.数列与函数、不等式结合例(2013年Ⅱ卷,理科第16题)等差数列{an}的前n项和为Sn ,已知S10=0,S15 =25,则nSn 的最小值为________.?4. 全国卷近年考题类型备课组的一些做法五.数列与函数、不等式结合??4. 全国卷近年考题类型备课组的一些做法备课组的一些做法5.高考导航 文科以等差、等比数列为主,侧重考查运算求解能力,理科以一般数列为主,并要求将其转化为等差、等比数列,侧重考查逻辑思维能力.
考查方式:一般是两道选填题或一道解答题,10~12分,大部份以中等题或容易题出现.若无解答题,一般在选填中将其设置为较难题.
备课组的一些做法5.高考导航 1、?等差、等比数列的通项公式、求和公式及性质是高考考查的重点,主要以选择题、填空题的形式出现在试题中,难度属中、低档,但解题方法灵活多样,掌握了一定的技巧,可以又快又准地完成,有利于区分出不同层次的学生。?
2、?解答题多是等差数列、等比数列与函数、不等式、方程、解析几何相联系的综合题,考查思维能力,解决问题的能力及综合运用数学思想方法的能力,综合性较强,难度一般不会太大。?
3、?数列的证明题是近年高考命题的又一大趋势,着重考察逻辑推理能力和综合运用知识解决问题的能力
4 、数列有关的应用题在高考题中经常出现,特别是数列建模问题,多与现实生活中的“增长率”及“贷款利率”等问题有关,常在客观题或解答题中出现。
?备课组的一些做法5.高考导航? 5、数列是考查探索能力、创新能力的极好素材,新颖、灵活的新试题经常出自数列。?
6、数列的求和和与数列的通项公式是研究数列的两个重要方面,本单元中公式主要涉及这两个方面,它们之间的关系一直是高考命题的热点,要充分重视,理解它们之间的转化与化归。
? 7、从解题思想方法的规律着眼,主要有:
①方程思想的应用,利用公式列方程(组),例如等差、等比数列中的“知三求二”问题;
②函数思想方法的应用、图像、单调性、最值等问题;③待定系数法、分类讨论等方法的应用.备课组的一些做法6.单元重点与难点重点:
数列通项公式的意义及求法, an与Sn的关系及应用;等差数列的判断,通项公式、
前n项和公式、等差数列的性质应用;等比数列的判断,通项公式和前n项和的公式以及等比数列的有关性质的应用.?
难点:
等比与等差的交汇知识,通项公式的求法,数列求和。备课组的一些做法7.考试方向预测?2.用数列知识解决实际问题,考查应用能力;
3.将数列与三角、或函数的奇偶性或导数结合;
4.将数列与常用逻辑用语结合;
5.构建新的数列,与函数、不等式等内容结合,设计有梯度的设问,以考查创新意识.三 .题组训练与小专题结合解答下列各题: 1.已知 ,若函数 有3个零点,
则实数m的取值范围是_______.2.f(x)是定义在R上的偶函数,对任意 ,都有f(x-2)=f(x+2),
且当 时, .若在区间(-2,6]内关于x的方程
恰有3个不同的实数根,
则实数a的取值范围是( )3. 已知 ,且函数 有且仅有两个零点,则实数a的取值范围是________.4.若函数 在区间 内有零点,则实数a的取值范围是________.?三 .题组训练与小专题结合??三 .题组训练与小专题结合???三 .题组训练与小专题结合??三 .题组训练与小专题结合??三 .题组训练与小专题结合四.分专题进行研究熟记常见结论,速解周期考题 结论1 若f(x+a)=f(x+b),则f(x)的一个周期是|a-b|.结论2 若f(x+a)=-f(x),则f(x)的一个周期是2|a|.结论3若 ,则f(x)的一个周期是2|a|.结论4若函数y=f(x)图像同时关于点A(a,c)和点B(b,c)成中心对称(a≠b),则y=f(x)的一个周期是2|a-b|.结论5 若函数y=f(x)图像同时关于直线x=a和直线x=b成轴对称(a≠b),则y=f(x)的一个周期是2|a-b|.结论6若函数y=f(x)图像既关于点A(a,c)成中心对称又关于直线x=b成轴对称(a≠b),则y=f(x)的一个周期是4|a-b|.结论7 若f(x)=f(x+a)+f(x-a),则y=f(x)的一个周期是6|a|.例6(2014新课标卷Ⅰ文科第21题)
设函数 曲线y=f(x)在点(1,f(1))处的切线斜率为0.
(Ⅱ)若存在x0≥1,使得 f(x0)< ,求a的取值范围.例7(2014浙江第21题)已知函数f(x)=x3+3|x-a|(a>0).若f(x)在[-1,1]上的最小值记为g(a).
(Ⅰ)求g(a);
(Ⅱ)证明:当x∈[-1,1]时,恒有f(x)≤g(a)+4.例8 (2013年新课标1理科)已知函数
,若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(Ⅱ)若x≥-2时,f(x)≤kg(x),求k的取值范围.存在、任意相关的恒成立问题四.分专题进行研究设c是常数,D、I分别表示函数f(x)或g(x)的定义域或其某一子集,则在中学数学内容内有下列结论: 存在、任意相关的恒成立问题四.分专题进行研究设c是常数,D、I分别表示函数f(x)或g(x)的定义域或其某一子集,则在中学数学内容内有下列结论: 4. 恒成立5. 恒成立6. 使得 成立存在、任意相关的恒成立问题四.分专题进行研究?解答 由f(x1)≤g(x2)得:于是f(x1)max≤c, c≤g(x2)max,故f(x1)max≤g(x2)max.c存在、任意相关的恒成立问题四.分专题进行研究单调性相关的恒成立问题?四.分专题进行研究?围绕核心问题,使用微单元教学椭圆C: 的离心率为 ,长轴端点与短轴端点间的距离为 .
(Ⅰ)求椭圆的方程;
(Ⅱ)过点D(0,4)的直线l与椭圆C交于两点E、F,
①设B(0, ),若|BE|=|BF|,求直线l的斜率;
②若|DE|= |DF|,求 的取值范围;
③A是椭圆的右顶点,且∠EAF的角平分线是x轴,求直线l的斜率;四.分专题进行研究④以线段OE、OF为邻边作平行四边形OEFP,其中顶点P在椭圆C上,O为坐标原点,求O到直线l的距离;
⑤若以EF为直径的圆过原点,求直线l的斜率;
⑥点M为直线 与椭圆C在第一象限的交点,平行于OM的直线l与交椭圆于点A、B两点,求证直线MA、MB与x轴始终围成一个等腰三角形;
⑦你还能提出哪些类似问题?四.分专题进行研究围绕核心问题,使用微单元教学概括以上问题的求解过程,填写下表:|BE|=|BF|等腰三角形、三线合一 kEFkBN=-1 (N是EF中点)∠EAF的角平分线是x轴直线AE、AF关于x轴对称kAE+kAF=0四.分专题进行研究围绕核心问题,使用微单元教学概括以上问题的求解过程,填写下表:以线段OE、OF为邻边作平行四边形OEFP,其中顶点P在椭圆C上直线MA、MB与x轴始终围成一个等腰三角形直线MA、MB关于
x=xM对称kMA+kMB=0以EF为直径的圆过原点四.分专题进行研究围绕核心问题,使用微单元教学五.研究高考题,与高考接轨1. 的图象与性质定义域为R,值域为 ,增区间为 ,减区间为 . 2014年天津理科20题,即是以此题为背景而编制的试题:已知函数 .已知函数y=f(x)有两个零点x1,x2且x1(Ⅰ)求a的取值范围;
(Ⅱ)证明: 随着a的减小而增大;
(Ⅲ)证明:x1+x2随着a的减小而增大. 2014年高考山东理科20题:2. 的图象与性质定义域为 ,值域为 .
当x>0时,在x=1时取得最小值e.
增区间为 ,减区间为 .设函数 (k为常数,e是自然对数的底数).
(Ⅰ)当k≤0时,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围. 五.研究高考题,与高考接轨3. 的图象与性质定义域为R,值域为 ,当x=-1时,
增区间为 ,减区间为 . 4. 的图象与性质定义域为R+,值域为 ,当x=e时,
增区间为 ,减区间为 . 五.研究高考题,与高考接轨5. 的图象与性质定义域为 ,值域为 .
当x>1时,在x=e时取得最小值e.
增区间为 ,减区间为 .6. 的图象与性质定义域为 ,值域为
当 时,
增区间为 ,减区间为五.研究高考题,与高考接轨7. 也可以研究更为一般的函数:
的性质. 2014年全国Ⅰ卷理科21题:
设函数 ,曲线y=f(x)在点(1,f(1))处的切线为y=e(x-1)+2.
(Ⅰ)求a,b;
(Ⅱ)证明:f(x)>1.五.研究高考题,与高考接轨函数y=f(x)在x=x0取得极值,y=f(x)的图象与直线y=h有两个交点x1、x2,由于y=f(x)在x=x0两侧的曲率不同,则有 ,怎样比较x0与 的大小或比较x02与x1x2的大小.这样的现象我们称之为极值点的偏移问题,这种问题在高考试题中经常见到.五.研究高考题,与高考接轨题型之一:与x1+x2相关例1 (2013年湖南文科21题):已知函数
(Ⅰ)求f(x)的单调区间;
(Ⅱ)证明:当f(x1)=f(x2) (x1≠x2)时,x1+x2<0.例2 (2011年辽宁理科21题)已知函数f(x)=lnx-ax2+(2-a)x.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)设a>0,证明:当 时,
(Ⅲ)若函数的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
证明:例3 (2015天府大联考9月Ⅱ卷21题)(理科) ,其中a≠0.
(Ⅲ)若存在两个异号实根x1,x2,求证:x1+x2>0.五.研究高考题,与高考接轨题型之一:与x1+x2相关?五.研究高考题,与高考接轨题型之一:与x1+x2相关结论:不难发现,都是先证关于极值点x0对称的两个函数值f(x+x0)与f(x0-x)的大小关系,于是一般地:
(1)构造一元差函数F(x)=f(x+x0)-f(x0-x);
(2)对求导,确定其单调性;
(3)结合F(0)=0,判断F(x)的符号,从而确定f(x+x0)与f(x0-x)的大小关系;
(4)由f(x1)=f(x2)=f(x0-(x0-x2))>0(或<0)f(x0+(x0-x2)),
得到f(x1)>(或0)f(2x0-x2);
(5)结合f(x)的单调性得到x1>(或<0)2x0-x2,即 >(或<)x0.五.研究高考题,与高考接轨例4 (2014天津理科20)设f(x)=x-aex (a∈R),x∈R.已知函数y=f(x)有两个零点x1,x2,且x1(Ⅲ)证明:x1+x2随着a的减小而增大. 题型之二: 与 相关例5(2015天府大联考9月Ⅱ卷21题)已知函数f(x)=xlnx (x>0),g(x)= ,点A(x1,y1),B(x2,y2),C(x3,y3) 为曲线y=g(x)上的三点,且0(Ⅱ)设直线AB的斜率为k,若 ,试证明五.研究高考题,与高考接轨例6 设f(x)=lnx-mx (m∈R),已知函数y=f(x)有两个零点x1,x2,且x1x2>e2.六.培养学生解题意识,提升思维的品质已知函数 ,求f(x)的单调区间. 解答 ,下面进行讨论. (1) a<0时;(2) a=0时;(3) a>0时;又分02进行讨论.2014四川高考文理科21题:
已知函数
其中,e=2.71828…为自然对数的底数.
(Ⅰ)设g(x)是函数f(x)的导函数,求函数g(x)在区间
[0,1]上的最小值.六.培养学生解题意识,提升思维的品质我解答完所有问题了吗?是否做了最后的检查?方程有解函数恒增为恒为减求函数的定义域,看参数的取值范围求导,令导数 在,则函数有增有减构建思路,分类作答方程有解还是无解不在,则函数恒增或恒减分析解析式特征先不急于求 明确做什么?能否直接判断导函数的正负怎样画草图?图象有无上界或下界?若方程无解根在定义域内吗??七.回归教材,重视例习题的研究七.回归教材,重视例习题的研究 高考命题源于教材,高于教材,回归教材的目的就是要寻源,教材是很好的母题库,几乎每一道高考试题都可以在教材中找到源头.?解法的探究? 中点弦是解析几何中的一类典型试题,可以很好地训练学生数形结合的思想、整体代换的思想,以及设而不求、点差法等处理问题的基本运算技巧.
试题内涵的拓展应用 如果我们能够在这道题的基础上再添加平时在考试中热门的几何元素,如三角形的面积问题,三角形的重心、对称问题,那就能拓展成高考题了.?试题内涵的拓展应用(Ⅲ)利用(Ⅱ)所揭示的椭圆几何性质,用作图方法找出下面给定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.
试题内涵的拓展应用?试题内涵的拓展应用设此椭圆的右顶点为Q,若直线l与椭圆交于A、B两点.如果△AQB的重心恰好是点G(0,-1),求直线l的方程.
试题内涵的拓展应用?链接高考? 通过对一道教材题目的探究可以看出,数学研究是永无止境的,一定要沉下心,多探究,用心去体会教材与高考试题间的联系,这对于提升课堂复习效率是大有裨益的.
3、回归教材,注重例习题的价值 例5 已知经过椭圆 的右焦点F2作垂直于 轴的直线AB,交椭圆于A、B两点,F1是椭圆的左焦点.
(Ⅰ)求△AF1B 的周长;
(Ⅱ)如果AB不垂直于 轴,△AF1B 的周长有变化吗?为什么?七.回归教材,重视例习题的研究例6 (2012年四川高考15题)椭圆 的左焦点F,直线 x=m与 椭圆交于A、B两点,当△AFB 的周长最大时,△AFB的面积是_____ . 例7 设点A(-5,0), B(5,0),直线AM,BM的斜率之积是 ,求动点M的轨迹方程. 设点A(-5,0), B(5,0),直线AM,BM的斜率之积是 ,求动点M的轨迹方程.七.回归教材,重视例习题的研究结论1 一动点与两定点连线的斜率之积为常数 .则
当 且 时,动点的轨迹是椭圆;
当 时,动点的轨迹是双曲线;
当 时,动点的轨迹是圆. (以上轨迹要去掉两定点) 结论2 设A、B是椭圆 的左、右顶点,其坐标为(-a,0)、(a,0),M是椭圆上异于A、B两点的任意点,则七.回归教材,重视例习题的研究结论3 设A、B是双曲线 的左右顶点,其坐标为(-a,0)、(a,0),M是椭圆上异于A、B两点的任意点,则结论4 设A、B是椭圆 上的两点,且点A、B关于原点对称,M是椭圆上异于A、B两点的任意点,则七.回归教材,重视例习题的研究结论5 设A、B是双曲线 上的两点,且点A、B关于原点对称,M是双曲线上异于A、B两点的任意点,则?七.回归教材,重视例习题的研究例9 (2011年江苏18题)如图,在平面直角坐标系xoy中,M、N分别是椭圆 的顶点,过坐标原点的直线交椭圆于P、A
两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k.
(Ⅰ)当直线PA平分线段MN时,求k的值;
(Ⅱ)当k=2时,求点P到直线AB的距离d;
(Ⅲ)对任意k>0,求证:PA⊥PB.揭示 (Ⅲ)由上面的结论知, ,经过简单的运算即可证得PA⊥PB.七.回归教材,重视例习题的研究谢谢!Thank you !
创建高效团队全国乙卷(Ⅰ卷)(理科)分析全国乙卷(Ⅰ卷)(理科)分析全国乙卷(Ⅰ卷)(理科)分析新增的不同于往年的考点:
第4题考查平时关注较少的几何概型:?全国乙卷(Ⅰ卷)(理科)分析第16题考查了应用型的线性规划:
某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为 元.
全国乙卷(Ⅰ卷)(理科)分析??全国乙卷(Ⅰ卷)(理科)分析二.立足基础,梯度合理
选择题前6个,属于简单试题,后面4个属于中档试题,最后两个难度较大,填空题前三个是简单题,最后一个需要很强的阅读提取信息的能力、建模和准确作图的能力,属于难题.
只要学生基石功扎实,17,18,19,20题第一问是较简单的基础题,20题第2问与21题有一定的难度,有较好的区分度.全国乙卷(Ⅰ卷)(理科)分析三.能力立意,适度创新
今年的试卷.对很多都要求学生有很好的思维能力,特别是创新意识的考查有所增加.
如第11题:?全国乙卷(Ⅰ卷)(理科)分析该题没有给出图形,考查了截面问题,面面平行的性质定理,异面直线所成的角,但载体是非常熟悉的正方体,加大了空间想象能力的考查,命题力求在继承中创新.全国乙卷(Ⅰ卷)(理科)分析 第4题与必修13第136页例1很相似,第16题线性规划与必修1第87页的引例如出一辙,是一个整点问题.
课本选修2-1第49页的习题:
圆O的半径为r,A是圆内一定点,P是圆上一动点,线段PA的垂直平分线与PO交于点Q,当点P在圆上运动时,点Q的轨迹是什么?为什么?全国乙卷(Ⅰ卷)(理科)分析?全国乙卷(Ⅰ卷)(理科)分析全国乙卷(Ⅰ卷)(理科)分析五.突出思想,注重通法
(3)已知等差数列{an}前9项的和为27,a10=8,则a100=
(A)100 (B)99 (C)98 (D)97?全国甲卷(Ⅱ卷理科)分析全国甲卷(Ⅱ卷)分析1.注意基础,平实近人
选择题前9个,填空题前3个与解答题前三个与选做题都是由基本知识、基本方法和常见材料构成.
2.立德树人,贴近实际
理科(5)
如图,小明从街道的E处出发,
先到F处与小红会合,再一起到
位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )
(A)24 (B)18 (C) 12 (D)9
全国甲卷(Ⅱ卷)分析?全国甲卷(Ⅱ卷)分析理科(8)与文科(9)
中国古代有计算多项式值的
秦九韶算法,下图是实现该算法
的程序框图.执行该程序框图,
若输入的x=2,n=2,依次输入的
为2,2,5,则输出的 ( )
(A)7 (B)12 (C)17 (D)34全国甲卷(Ⅱ卷)分析文科(18) 某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
(Ⅰ)记A为事件:“一续保人本年度的保费不高于基本保费”.求P(A)的估计值;
(Ⅱ)记B为事件:“一续保人本年 度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;
(Ⅲ)求续保人本年度的平均保费估计值.
全国甲卷(Ⅱ卷)分析3.体现差异,文理联姻
相对简单的题,全卷有6个题是相同的试题,相对较难的试题往往成为血缘题或姐妹题,全卷不同的题有13道.
4.依据课标,重视教材
引导我们要重视教材的学习,而不是考什么才学什么,而是学了什么才考什么,学了不一定考,不学也可能考,考的一定是学过的,不考的也可能是要求学的.让学生多一些知识的积累,多一些视野,多一些思考,多一些智慧和力量.全国甲卷(Ⅱ卷)分析 课标中要求:通过阅读中国古代数学中的算法案例,体会中国古代数学对世界数学发展的贡献.今年文科与理科都考查了秦九韶算法.
课标中说:了解随机数的意义,能运用模拟方法(包括计算器产生随机数来进行模拟)估计概率,初步体会几何概型的意义.教材中也有利用这种方法计算圆周率的例题.这要求教师改变教学方式,落实课标要求,回归教材,规避教辅资料.全国甲卷(Ⅱ卷)分析?全国甲卷(Ⅱ卷)分析5.回避套路,强调能力
一类题没在公理、没有原理、没有运算、没有成熟的解题套路,需要的是学生的逻辑推理能力.这种通过所学基础知识,获得解决问题的方法并能运用之解决生活实际中遇到的问题,正是我们希望学生所具有的能力.全国甲卷(Ⅱ卷)分析文科(16)与理科(15)
有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是 .全国甲卷(Ⅱ卷)分析2014年全国Ⅰ卷,文科与理科14题:
甲、乙、丙三位同学被问到是否去过A,B,C三个城市时,
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市;
丙说:我们三人去过同一个城市.
由此可判断乙去过的城市为 .全国甲卷(Ⅱ卷)分析6.易题求新,难题重质
17.(理科)
Sn为等差数列{an}的前n项和,且a1=1,S7=28,记bn=[lgan],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg99]=1.
(Ⅰ)求b1,b11,b101;
(Ⅱ)求数列{bn}的前1 000项和.全国甲卷(Ⅱ卷)分析17.(文科)
等差数列{an}中,a3+a4=4,a5+a7=6.
(Ⅰ)求{an}的通项公式;
(Ⅱ) 设bn=[an],求数列{bn}的前10项和,其中[x]表示不超过x的最大整数,如[0.9]=0,[2.6]=2.这本是两个难度较小的试题,但在学生熟悉的数列中巧妙地引入高斯函数,突然使此题摆脱了平庸.全国甲卷(Ⅱ卷)分析全国甲卷(Ⅱ卷)分析7.注意素养,考查思想
全卷注重对数学核心素养的考查,除对数学抽象、逻辑推理、直观想象、数学运算、数据分析、数学建模等六个核心素养的考查外,特别对数学思想与方法进行了考查.如:全国甲卷(Ⅱ卷)分析?解答 由f(-x)=2-f(x)马上构造一个函数f(x)=x+1即可.
这是典型的特殊与一般的思想的应用.若数形结合能力好的学生立即可得到函数f(x)关于点(0,1)对称.全国甲卷(Ⅱ卷)分析?全国甲卷(Ⅱ卷)分析理科20与文科21题第一问,利用数形结合很容易看到AM与AN的对称性,从而问题很好解决.全国甲卷(Ⅱ卷)分析备课组的一些做法一.加强集合备课,任务分工明确.备课组的一些做法一.加强集合备课,任务分工明确.备课组的一些做法一.加强集合备课,任务分工明确.备课组的一些做法一.加强集合备课,任务分工明确.南山中学2017级高三
数学纠错卡备课组的一些做法二. 集体备课模式(以数列为例)一.考纲要求
1.了解数列的概念与几种表示法
2.理解、掌握等差、等比数列的概念通项公式与前n项和公式
3.能在具体的情境中识别数列的等差关系或等比关系
4.能用等差、等比数列的相关知识解决相应的实际问题
5.了解等差数列与一次函数的关系、等比数列的指数函数的关系2. 集体备课的模式(以数列为例)备课组的一些做法备课组的一些做法二. 集体备课模式(以数列为例)3.知识网络备课组的一些做法4. 全国卷近年考题类型?备课组的一些做法?4. 全国卷近年考题类型备课组的一些做法二.等差数列、等比数列的相关公式及其性质的考查
例5 (2016年全国Ⅱ卷,理科17题)Sn为等差数列{an}的前n项和,且a1=1,S7=28,记bn=[lgan],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg99]=1.
(Ⅰ)求b1,b11,b101;
(Ⅱ)求数列{bn}的前1 000项和.
例6 (2016年全国Ⅱ卷,文科第17题)等差数列{an}中,a3+a4=4,a5+a7=6.
(Ⅰ)求{an}的通项公式;
(Ⅱ) 设bn=[an],求数列{bn}的前10项和,其中[x]表示不超过x的最大整数,如[0.9]=0,[2.6]=2.4. 全国卷近年考题类型备课组的一些做法三.运用累差叠加法、错位相减法、裂项法求和4. 全国卷近年考题类型备课组的一些做法三.运用累差叠加法、错位相减法、裂项法求和4. 全国卷近年考题类型备课组的一些做法四.Sn与an关系的运用4. 全国卷近年考题类型备课组的一些做法四.Sn与an关系的运用4. 全国卷近年考题类型备课组的一些做法五.数列与函数、不等式结合例(2013年Ⅱ卷,理科第16题)等差数列{an}的前n项和为Sn ,已知S10=0,S15 =25,则nSn 的最小值为________.?4. 全国卷近年考题类型备课组的一些做法五.数列与函数、不等式结合??4. 全国卷近年考题类型备课组的一些做法备课组的一些做法5.高考导航 文科以等差、等比数列为主,侧重考查运算求解能力,理科以一般数列为主,并要求将其转化为等差、等比数列,侧重考查逻辑思维能力.
考查方式:一般是两道选填题或一道解答题,10~12分,大部份以中等题或容易题出现.若无解答题,一般在选填中将其设置为较难题.
备课组的一些做法5.高考导航 1、?等差、等比数列的通项公式、求和公式及性质是高考考查的重点,主要以选择题、填空题的形式出现在试题中,难度属中、低档,但解题方法灵活多样,掌握了一定的技巧,可以又快又准地完成,有利于区分出不同层次的学生。?
2、?解答题多是等差数列、等比数列与函数、不等式、方程、解析几何相联系的综合题,考查思维能力,解决问题的能力及综合运用数学思想方法的能力,综合性较强,难度一般不会太大。?
3、?数列的证明题是近年高考命题的又一大趋势,着重考察逻辑推理能力和综合运用知识解决问题的能力
4 、数列有关的应用题在高考题中经常出现,特别是数列建模问题,多与现实生活中的“增长率”及“贷款利率”等问题有关,常在客观题或解答题中出现。
?备课组的一些做法5.高考导航? 5、数列是考查探索能力、创新能力的极好素材,新颖、灵活的新试题经常出自数列。?
6、数列的求和和与数列的通项公式是研究数列的两个重要方面,本单元中公式主要涉及这两个方面,它们之间的关系一直是高考命题的热点,要充分重视,理解它们之间的转化与化归。
? 7、从解题思想方法的规律着眼,主要有:
①方程思想的应用,利用公式列方程(组),例如等差、等比数列中的“知三求二”问题;
②函数思想方法的应用、图像、单调性、最值等问题;③待定系数法、分类讨论等方法的应用.备课组的一些做法6.单元重点与难点重点:
数列通项公式的意义及求法, an与Sn的关系及应用;等差数列的判断,通项公式、
前n项和公式、等差数列的性质应用;等比数列的判断,通项公式和前n项和的公式以及等比数列的有关性质的应用.?
难点:
等比与等差的交汇知识,通项公式的求法,数列求和。备课组的一些做法7.考试方向预测?2.用数列知识解决实际问题,考查应用能力;
3.将数列与三角、或函数的奇偶性或导数结合;
4.将数列与常用逻辑用语结合;
5.构建新的数列,与函数、不等式等内容结合,设计有梯度的设问,以考查创新意识.三 .题组训练与小专题结合解答下列各题: 1.已知 ,若函数 有3个零点,
则实数m的取值范围是_______.2.f(x)是定义在R上的偶函数,对任意 ,都有f(x-2)=f(x+2),
且当 时, .若在区间(-2,6]内关于x的方程
恰有3个不同的实数根,
则实数a的取值范围是( )3. 已知 ,且函数 有且仅有两个零点,则实数a的取值范围是________.4.若函数 在区间 内有零点,则实数a的取值范围是________.?三 .题组训练与小专题结合??三 .题组训练与小专题结合???三 .题组训练与小专题结合??三 .题组训练与小专题结合??三 .题组训练与小专题结合四.分专题进行研究熟记常见结论,速解周期考题 结论1 若f(x+a)=f(x+b),则f(x)的一个周期是|a-b|.结论2 若f(x+a)=-f(x),则f(x)的一个周期是2|a|.结论3若 ,则f(x)的一个周期是2|a|.结论4若函数y=f(x)图像同时关于点A(a,c)和点B(b,c)成中心对称(a≠b),则y=f(x)的一个周期是2|a-b|.结论5 若函数y=f(x)图像同时关于直线x=a和直线x=b成轴对称(a≠b),则y=f(x)的一个周期是2|a-b|.结论6若函数y=f(x)图像既关于点A(a,c)成中心对称又关于直线x=b成轴对称(a≠b),则y=f(x)的一个周期是4|a-b|.结论7 若f(x)=f(x+a)+f(x-a),则y=f(x)的一个周期是6|a|.例6(2014新课标卷Ⅰ文科第21题)
设函数 曲线y=f(x)在点(1,f(1))处的切线斜率为0.
(Ⅱ)若存在x0≥1,使得 f(x0)< ,求a的取值范围.例7(2014浙江第21题)已知函数f(x)=x3+3|x-a|(a>0).若f(x)在[-1,1]上的最小值记为g(a).
(Ⅰ)求g(a);
(Ⅱ)证明:当x∈[-1,1]时,恒有f(x)≤g(a)+4.例8 (2013年新课标1理科)已知函数
,若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(Ⅱ)若x≥-2时,f(x)≤kg(x),求k的取值范围.存在、任意相关的恒成立问题四.分专题进行研究设c是常数,D、I分别表示函数f(x)或g(x)的定义域或其某一子集,则在中学数学内容内有下列结论: 存在、任意相关的恒成立问题四.分专题进行研究设c是常数,D、I分别表示函数f(x)或g(x)的定义域或其某一子集,则在中学数学内容内有下列结论: 4. 恒成立5. 恒成立6. 使得 成立存在、任意相关的恒成立问题四.分专题进行研究?解答 由f(x1)≤g(x2)得:于是f(x1)max≤c, c≤g(x2)max,故f(x1)max≤g(x2)max.c存在、任意相关的恒成立问题四.分专题进行研究单调性相关的恒成立问题?四.分专题进行研究?围绕核心问题,使用微单元教学椭圆C: 的离心率为 ,长轴端点与短轴端点间的距离为 .
(Ⅰ)求椭圆的方程;
(Ⅱ)过点D(0,4)的直线l与椭圆C交于两点E、F,
①设B(0, ),若|BE|=|BF|,求直线l的斜率;
②若|DE|= |DF|,求 的取值范围;
③A是椭圆的右顶点,且∠EAF的角平分线是x轴,求直线l的斜率;四.分专题进行研究④以线段OE、OF为邻边作平行四边形OEFP,其中顶点P在椭圆C上,O为坐标原点,求O到直线l的距离;
⑤若以EF为直径的圆过原点,求直线l的斜率;
⑥点M为直线 与椭圆C在第一象限的交点,平行于OM的直线l与交椭圆于点A、B两点,求证直线MA、MB与x轴始终围成一个等腰三角形;
⑦你还能提出哪些类似问题?四.分专题进行研究围绕核心问题,使用微单元教学概括以上问题的求解过程,填写下表:|BE|=|BF|等腰三角形、三线合一 kEFkBN=-1 (N是EF中点)∠EAF的角平分线是x轴直线AE、AF关于x轴对称kAE+kAF=0四.分专题进行研究围绕核心问题,使用微单元教学概括以上问题的求解过程,填写下表:以线段OE、OF为邻边作平行四边形OEFP,其中顶点P在椭圆C上直线MA、MB与x轴始终围成一个等腰三角形直线MA、MB关于
x=xM对称kMA+kMB=0以EF为直径的圆过原点四.分专题进行研究围绕核心问题,使用微单元教学五.研究高考题,与高考接轨1. 的图象与性质定义域为R,值域为 ,增区间为 ,减区间为 . 2014年天津理科20题,即是以此题为背景而编制的试题:已知函数 .已知函数y=f(x)有两个零点x1,x2且x1
(Ⅱ)证明: 随着a的减小而增大;
(Ⅲ)证明:x1+x2随着a的减小而增大. 2014年高考山东理科20题:2. 的图象与性质定义域为 ,值域为 .
当x>0时,在x=1时取得最小值e.
增区间为 ,减区间为 .设函数 (k为常数,e是自然对数的底数).
(Ⅰ)当k≤0时,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围. 五.研究高考题,与高考接轨3. 的图象与性质定义域为R,值域为 ,当x=-1时,
增区间为 ,减区间为 . 4. 的图象与性质定义域为R+,值域为 ,当x=e时,
增区间为 ,减区间为 . 五.研究高考题,与高考接轨5. 的图象与性质定义域为 ,值域为 .
当x>1时,在x=e时取得最小值e.
增区间为 ,减区间为 .6. 的图象与性质定义域为 ,值域为
当 时,
增区间为 ,减区间为五.研究高考题,与高考接轨7. 也可以研究更为一般的函数:
的性质. 2014年全国Ⅰ卷理科21题:
设函数 ,曲线y=f(x)在点(1,f(1))处的切线为y=e(x-1)+2.
(Ⅰ)求a,b;
(Ⅱ)证明:f(x)>1.五.研究高考题,与高考接轨函数y=f(x)在x=x0取得极值,y=f(x)的图象与直线y=h有两个交点x1、x2,由于y=f(x)在x=x0两侧的曲率不同,则有 ,怎样比较x0与 的大小或比较x02与x1x2的大小.这样的现象我们称之为极值点的偏移问题,这种问题在高考试题中经常见到.五.研究高考题,与高考接轨题型之一:与x1+x2相关例1 (2013年湖南文科21题):已知函数
(Ⅰ)求f(x)的单调区间;
(Ⅱ)证明:当f(x1)=f(x2) (x1≠x2)时,x1+x2<0.例2 (2011年辽宁理科21题)已知函数f(x)=lnx-ax2+(2-a)x.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)设a>0,证明:当 时,
(Ⅲ)若函数的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
证明:例3 (2015天府大联考9月Ⅱ卷21题)(理科) ,其中a≠0.
(Ⅲ)若存在两个异号实根x1,x2,求证:x1+x2>0.五.研究高考题,与高考接轨题型之一:与x1+x2相关?五.研究高考题,与高考接轨题型之一:与x1+x2相关结论:不难发现,都是先证关于极值点x0对称的两个函数值f(x+x0)与f(x0-x)的大小关系,于是一般地:
(1)构造一元差函数F(x)=f(x+x0)-f(x0-x);
(2)对求导,确定其单调性;
(3)结合F(0)=0,判断F(x)的符号,从而确定f(x+x0)与f(x0-x)的大小关系;
(4)由f(x1)=f(x2)=f(x0-(x0-x2))>0(或<0)f(x0+(x0-x2)),
得到f(x1)>(或0)f(2x0-x2);
(5)结合f(x)的单调性得到x1>(或<0)2x0-x2,即 >(或<)x0.五.研究高考题,与高考接轨例4 (2014天津理科20)设f(x)=x-aex (a∈R),x∈R.已知函数y=f(x)有两个零点x1,x2,且x1
已知函数
其中,e=2.71828…为自然对数的底数.
(Ⅰ)设g(x)是函数f(x)的导函数,求函数g(x)在区间
[0,1]上的最小值.六.培养学生解题意识,提升思维的品质我解答完所有问题了吗?是否做了最后的检查?方程有解函数恒增为恒为减求函数的定义域,看参数的取值范围求导,令导数 在,则函数有增有减构建思路,分类作答方程有解还是无解不在,则函数恒增或恒减分析解析式特征先不急于求 明确做什么?能否直接判断导函数的正负怎样画草图?图象有无上界或下界?若方程无解根在定义域内吗??七.回归教材,重视例习题的研究七.回归教材,重视例习题的研究 高考命题源于教材,高于教材,回归教材的目的就是要寻源,教材是很好的母题库,几乎每一道高考试题都可以在教材中找到源头.?解法的探究? 中点弦是解析几何中的一类典型试题,可以很好地训练学生数形结合的思想、整体代换的思想,以及设而不求、点差法等处理问题的基本运算技巧.
试题内涵的拓展应用 如果我们能够在这道题的基础上再添加平时在考试中热门的几何元素,如三角形的面积问题,三角形的重心、对称问题,那就能拓展成高考题了.?试题内涵的拓展应用(Ⅲ)利用(Ⅱ)所揭示的椭圆几何性质,用作图方法找出下面给定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.
试题内涵的拓展应用?试题内涵的拓展应用设此椭圆的右顶点为Q,若直线l与椭圆交于A、B两点.如果△AQB的重心恰好是点G(0,-1),求直线l的方程.
试题内涵的拓展应用?链接高考? 通过对一道教材题目的探究可以看出,数学研究是永无止境的,一定要沉下心,多探究,用心去体会教材与高考试题间的联系,这对于提升课堂复习效率是大有裨益的.
3、回归教材,注重例习题的价值 例5 已知经过椭圆 的右焦点F2作垂直于 轴的直线AB,交椭圆于A、B两点,F1是椭圆的左焦点.
(Ⅰ)求△AF1B 的周长;
(Ⅱ)如果AB不垂直于 轴,△AF1B 的周长有变化吗?为什么?七.回归教材,重视例习题的研究例6 (2012年四川高考15题)椭圆 的左焦点F,直线 x=m与 椭圆交于A、B两点,当△AFB 的周长最大时,△AFB的面积是_____ . 例7 设点A(-5,0), B(5,0),直线AM,BM的斜率之积是 ,求动点M的轨迹方程. 设点A(-5,0), B(5,0),直线AM,BM的斜率之积是 ,求动点M的轨迹方程.七.回归教材,重视例习题的研究结论1 一动点与两定点连线的斜率之积为常数 .则
当 且 时,动点的轨迹是椭圆;
当 时,动点的轨迹是双曲线;
当 时,动点的轨迹是圆. (以上轨迹要去掉两定点) 结论2 设A、B是椭圆 的左、右顶点,其坐标为(-a,0)、(a,0),M是椭圆上异于A、B两点的任意点,则七.回归教材,重视例习题的研究结论3 设A、B是双曲线 的左右顶点,其坐标为(-a,0)、(a,0),M是椭圆上异于A、B两点的任意点,则结论4 设A、B是椭圆 上的两点,且点A、B关于原点对称,M是椭圆上异于A、B两点的任意点,则七.回归教材,重视例习题的研究结论5 设A、B是双曲线 上的两点,且点A、B关于原点对称,M是双曲线上异于A、B两点的任意点,则?七.回归教材,重视例习题的研究例9 (2011年江苏18题)如图,在平面直角坐标系xoy中,M、N分别是椭圆 的顶点,过坐标原点的直线交椭圆于P、A
两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k.
(Ⅰ)当直线PA平分线段MN时,求k的值;
(Ⅱ)当k=2时,求点P到直线AB的距离d;
(Ⅲ)对任意k>0,求证:PA⊥PB.揭示 (Ⅲ)由上面的结论知, ,经过简单的运算即可证得PA⊥PB.七.回归教材,重视例习题的研究谢谢!Thank you !
同课章节目录
