18.2勾股定理的逆定理1
文档属性
| 名称 | 18.2勾股定理的逆定理1 |  | |
| 格式 | rar | ||
| 文件大小 | 338.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-11 19:52:00 | ||
图片预览





文档简介
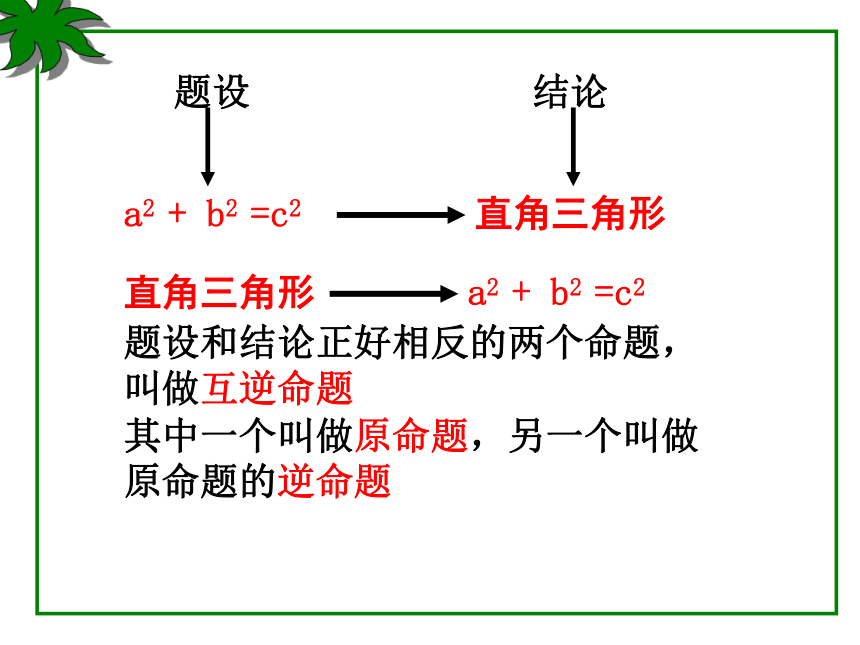
课件24张PPT。勾股定理的逆定理题设:直角三角形的两直角边长分别为a、b,斜边长为c结论:a2+b2=c2命题:题设和结论正好相反的两个命题, 叫做互逆命题其中一个叫做原命题,另一个叫做
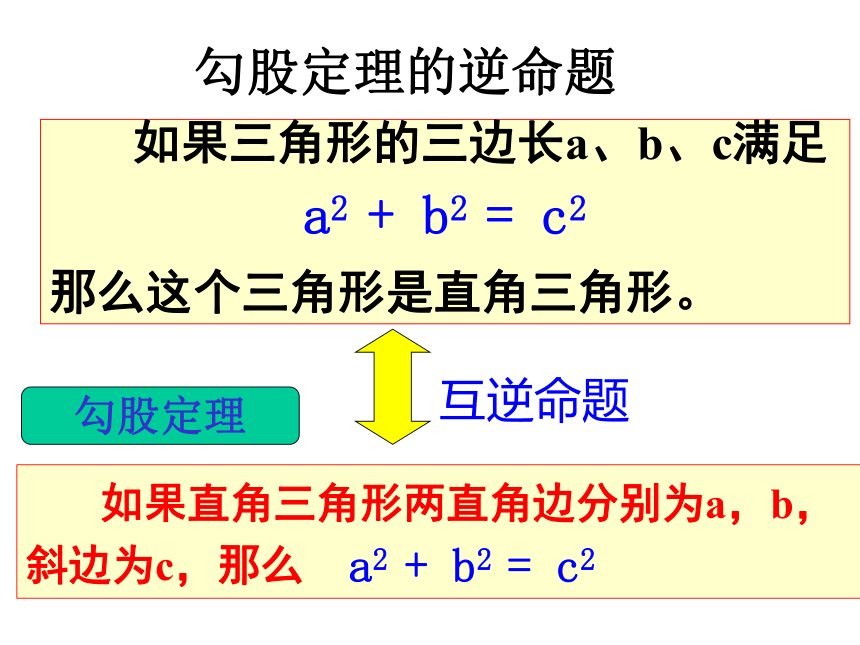
原命题的逆命题 勾股定理的逆命题勾股定理互逆命题(1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的平方相等.
(3)如果两个实数相等,那么它们的绝对值相等.
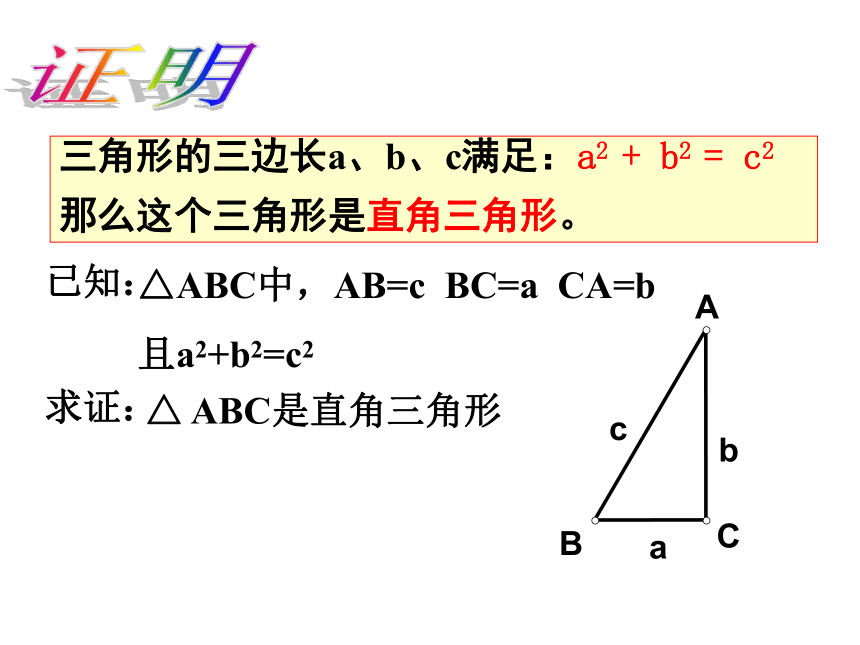
(4)全等三角形的对应角相等.说出下列命题的逆命题.这些命题的逆命题成立吗?逆命题: 内错角相等,两条直线平行. 逆命题:如果两个实数的平方相等,那么这两个实数相等. 逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 逆命题:对应角相等的两个三角形是全等三角形. 感悟: 原命题成立时, 逆命题有时成立, 有时不成立一个命题是真命题,它逆命题却不一定是真命题.成立不成立不成立不成立 古埃及人把一根绳子打上等距离的13个结,然后把第1个结和第13个结用木桩钉在一起,再分别用木桩把第4个结和第8个结钉牢(拉直绳子)。三角形的三边有什么关系呢?探索新知你能猜想出其中的数学道理吗?证明三角形的三边长a、b、c满足:a2 + b2 = c2
那么这个三角形是直角三角形。已知:△ABC中,AB=c BC=a CA=b
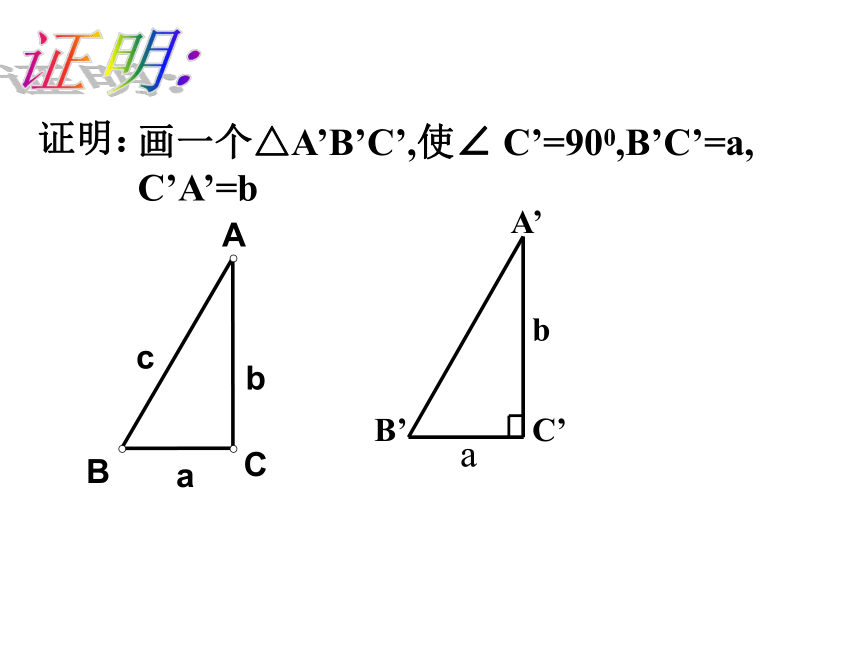
且a2+b2=c2求证:△ ABC是直角三角形证明:画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=bC’A’B’ab证明:勾股定理的逆命题勾股定理互逆命题(逆定理)(互逆定理)驶向胜利的彼岸定理与逆定理我们已经学习了一些互逆的定理,如:
勾股定理及其逆定理,
两直线平行,内错角相等;内错角相等,两直线平行.想一想:
互逆命题与互逆定理有何关系?如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.三角形的三边长a、b、c满足:a2 + b2 = c2
那么这个三角形是直角三角形。知识驿站勾股定理逆定理例1 判断由a、b、c组成的三角形是不是直角三角形:
(1) a=15 , b =8 , c=17(2) a=13 , b =15 , c=14分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方。应用新知1、工厂生产的产品都有一定的规格要求,如图所示:该模板中的AB、BC 相交成直角才符合规定。你能测出这个零件是否合格呢?(身边
只有刻度尺) 2、下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ; 像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数. 3、如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。24平方米
4、 已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
S四边形ABCD=36应用拓展:如图:边长为4的正方形ABCD中,F是DC的中
点,且CE= BC,则AF⊥EF,试说明理由解:连接AE
∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC∴根据勾股定理,在
Rt△ADF,AF2=AD2+DF2=20
Rt△EFC,EF2=EC2+FC2=5
Rt△ABE,AE2=AB2+BE2=25∴AD=4,DF=2,FC=2,EC=1∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EF分析:先来判断a,b,c三边哪条最长,可以代m,n为满足条件的特殊值来试,m=5,n=4.则a=9,b=40,c=41,c最大。∴△ABC是直角三角形(一)选择题: 练 习 1.在已知下列三组长度的线段中,不能构
成直角三角形的是 ( )
(A)5、12、13 (B)2、3、
(C)4、7、5 (D)1、 、 C (一)选择题: 练 习 2.下列命题中,假命题是 ( )
(A)三个角的度数之比为1 : 3 : 4的三角形是直角三角形
(B)三个角的度数之比为1 : : 2的三角形是直角三角形
(C)三边长度之比为1 : : 2的三角形是直角三角形
(D)三边长度之比为 : : 2的三角形是直角三角形 B 1.如果△ABC的三边分别为a、b、c且满足
a2+b2+c2+50=6a+8b+10c,
判定△ABC的形状. (二)解答题: 练 习 这个三角形是直角三角形. 小游戏3、以小组为单位,每位同学自己找一组
勾股数,那一组找的最快最多就算获胜。加油谈谈这节课你的收获吧!
原命题的逆命题 勾股定理的逆命题勾股定理互逆命题(1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的平方相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应角相等.说出下列命题的逆命题.这些命题的逆命题成立吗?逆命题: 内错角相等,两条直线平行. 逆命题:如果两个实数的平方相等,那么这两个实数相等. 逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 逆命题:对应角相等的两个三角形是全等三角形. 感悟: 原命题成立时, 逆命题有时成立, 有时不成立一个命题是真命题,它逆命题却不一定是真命题.成立不成立不成立不成立 古埃及人把一根绳子打上等距离的13个结,然后把第1个结和第13个结用木桩钉在一起,再分别用木桩把第4个结和第8个结钉牢(拉直绳子)。三角形的三边有什么关系呢?探索新知你能猜想出其中的数学道理吗?证明三角形的三边长a、b、c满足:a2 + b2 = c2
那么这个三角形是直角三角形。已知:△ABC中,AB=c BC=a CA=b
且a2+b2=c2求证:△ ABC是直角三角形证明:画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=bC’A’B’ab证明:勾股定理的逆命题勾股定理互逆命题(逆定理)(互逆定理)驶向胜利的彼岸定理与逆定理我们已经学习了一些互逆的定理,如:
勾股定理及其逆定理,
两直线平行,内错角相等;内错角相等,两直线平行.想一想:
互逆命题与互逆定理有何关系?如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.三角形的三边长a、b、c满足:a2 + b2 = c2
那么这个三角形是直角三角形。知识驿站勾股定理逆定理例1 判断由a、b、c组成的三角形是不是直角三角形:
(1) a=15 , b =8 , c=17(2) a=13 , b =15 , c=14分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方。应用新知1、工厂生产的产品都有一定的规格要求,如图所示:该模板中的AB、BC 相交成直角才符合规定。你能测出这个零件是否合格呢?(身边
只有刻度尺) 2、下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ; 像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数. 3、如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。24平方米
4、 已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
S四边形ABCD=36应用拓展:如图:边长为4的正方形ABCD中,F是DC的中
点,且CE= BC,则AF⊥EF,试说明理由解:连接AE
∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC∴根据勾股定理,在
Rt△ADF,AF2=AD2+DF2=20
Rt△EFC,EF2=EC2+FC2=5
Rt△ABE,AE2=AB2+BE2=25∴AD=4,DF=2,FC=2,EC=1∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EF分析:先来判断a,b,c三边哪条最长,可以代m,n为满足条件的特殊值来试,m=5,n=4.则a=9,b=40,c=41,c最大。∴△ABC是直角三角形(一)选择题: 练 习 1.在已知下列三组长度的线段中,不能构
成直角三角形的是 ( )
(A)5、12、13 (B)2、3、
(C)4、7、5 (D)1、 、 C (一)选择题: 练 习 2.下列命题中,假命题是 ( )
(A)三个角的度数之比为1 : 3 : 4的三角形是直角三角形
(B)三个角的度数之比为1 : : 2的三角形是直角三角形
(C)三边长度之比为1 : : 2的三角形是直角三角形
(D)三边长度之比为 : : 2的三角形是直角三角形 B 1.如果△ABC的三边分别为a、b、c且满足
a2+b2+c2+50=6a+8b+10c,
判定△ABC的形状. (二)解答题: 练 习 这个三角形是直角三角形. 小游戏3、以小组为单位,每位同学自己找一组
勾股数,那一组找的最快最多就算获胜。加油谈谈这节课你的收获吧!
