数学五年级上青岛版5.10回顾整理—多边形的面积课件(27张)
文档属性
| 名称 | 数学五年级上青岛版5.10回顾整理—多边形的面积课件(27张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-24 20:15:00 | ||
图片预览


文档简介
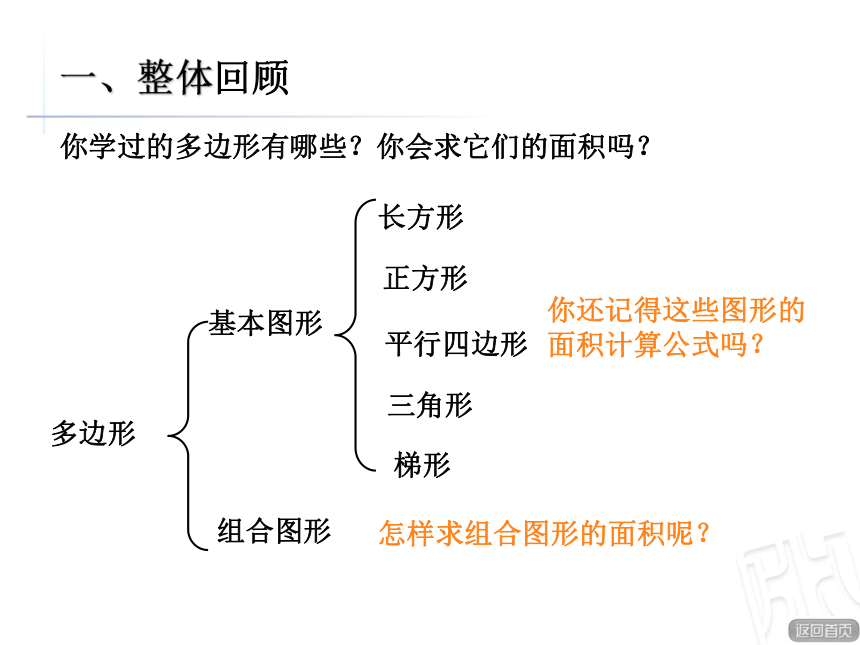
课件27张PPT。Nz基本图形一、整体回顾
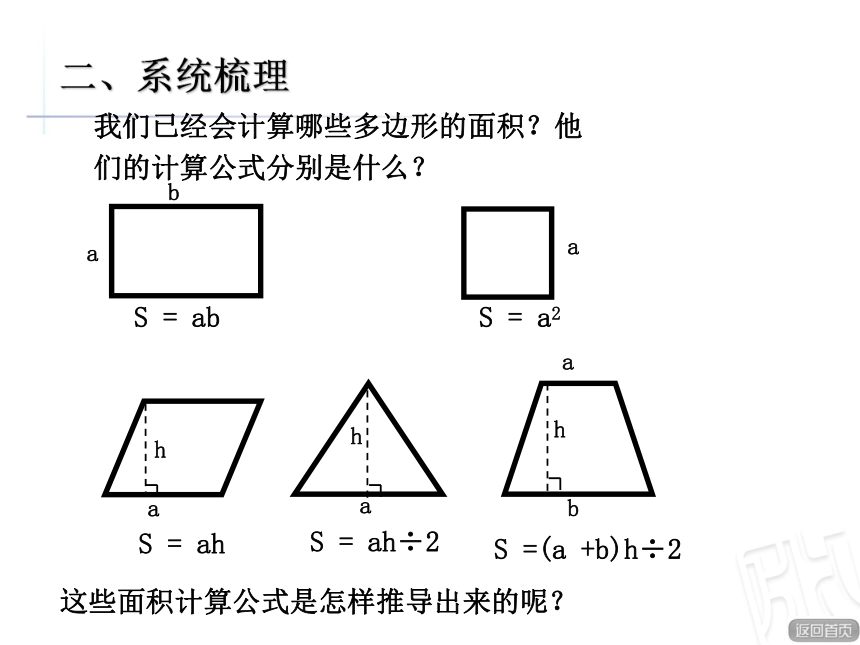
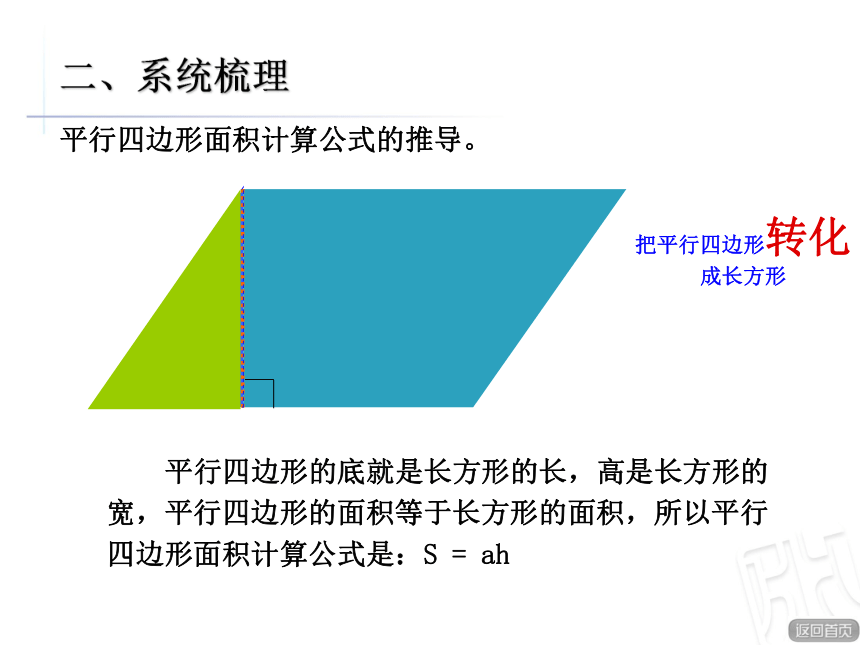
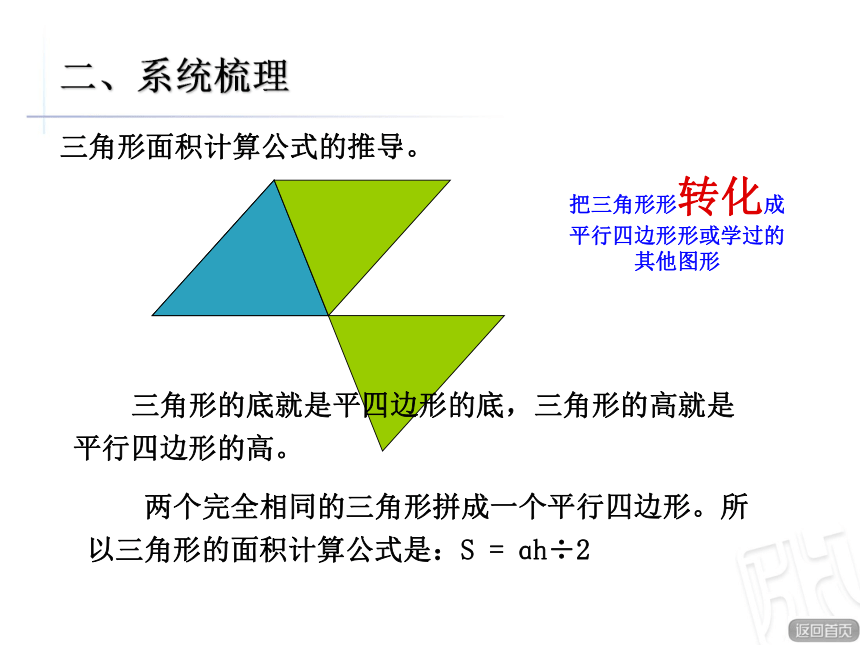
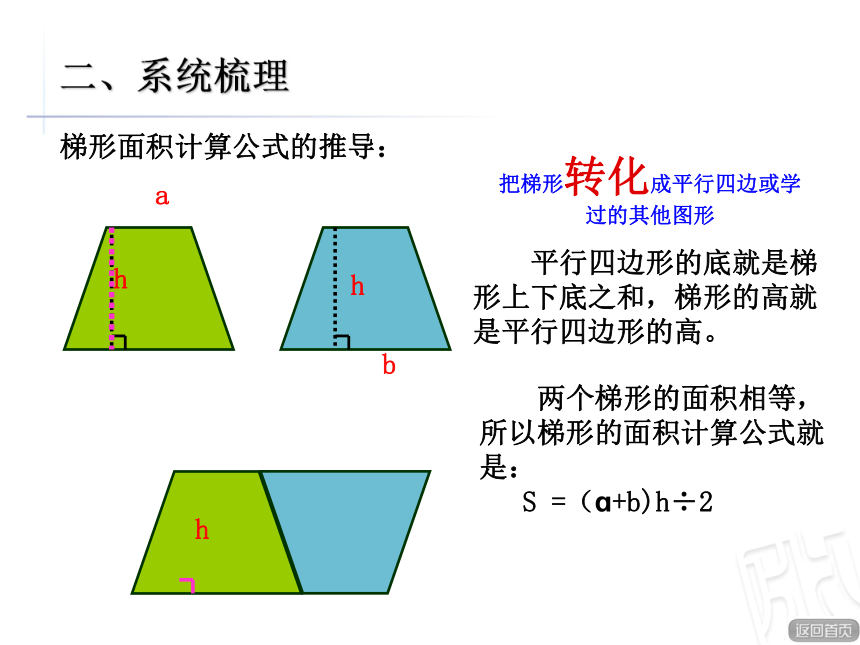
多边形组合图形长方形正方形平行四边形三角形梯形你学过的多边形有哪些?你会求它们的面积吗?你还记得这些图形的面积计算公式吗?怎样求组合图形的面积呢?我们已经会计算哪些多边形的面积?他们的计算公式分别是什么?baS = ab aS = a2haS = ah S =(a +b)h÷2 abhahS = ah÷2 二、系统梳理这些面积计算公式是怎样推导出来的呢?长方形和正方形面积计算公式的推导。ɑbS= ab 一个正方形的面积是1平方厘米,长方形一共有b行,a列。所以长方形的面积计算公式是:S = ab。二、系统梳理 正方形是特殊的长方形,当a = b时,正方形的面积计算公式是:S = a2数方格的方法平行四边形面积计算公式的推导。 平行四边形的底就是长方形的长,高是长方形的宽,平行四边形的面积等于长方形的面积,所以平行四边形面积计算公式是:S = ah 二、系统梳理把平行四边形转化成长方形三角形面积计算公式的推导。 三角形的底就是平四边形的底,三角形的高就是平行四边形的高。二、系统梳理 两个完全相同的三角形拼成一个平行四边形。所以三角形的面积计算公式是:S = ɑh÷2 把三角形形转化成平行四边形形或学过的其他图形abhhh梯形面积计算公式的推导: 平行四边形的底就是梯形上下底之和,梯形的高就是平行四边形的高。二、系统梳理 两个梯形的面积相等,所以梯形的面积计算公式就是:
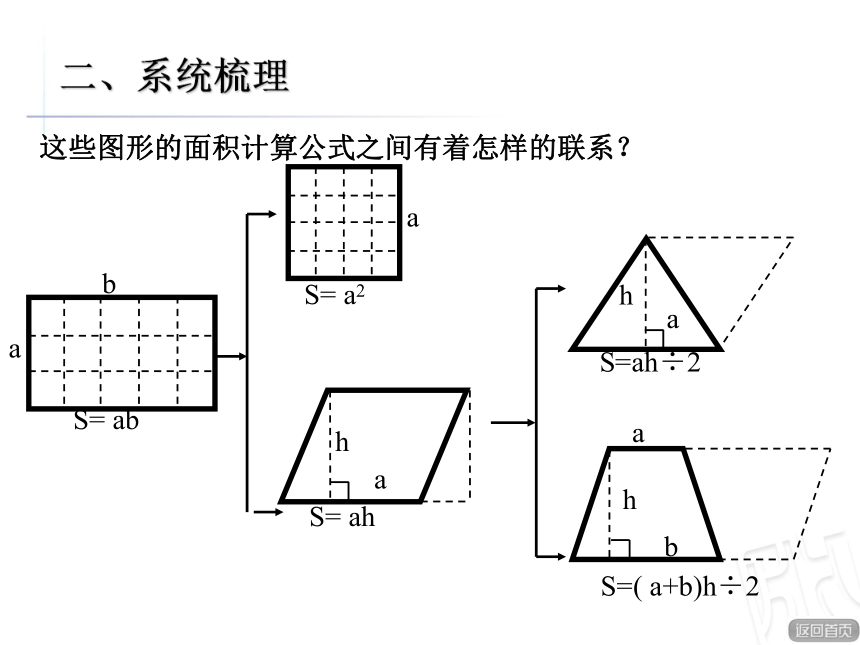
S =(ɑ+b)h÷2把梯形转化成平行四边或学过的其他图形这些图形的面积计算公式之间有着怎样的联系?二、系统梳理
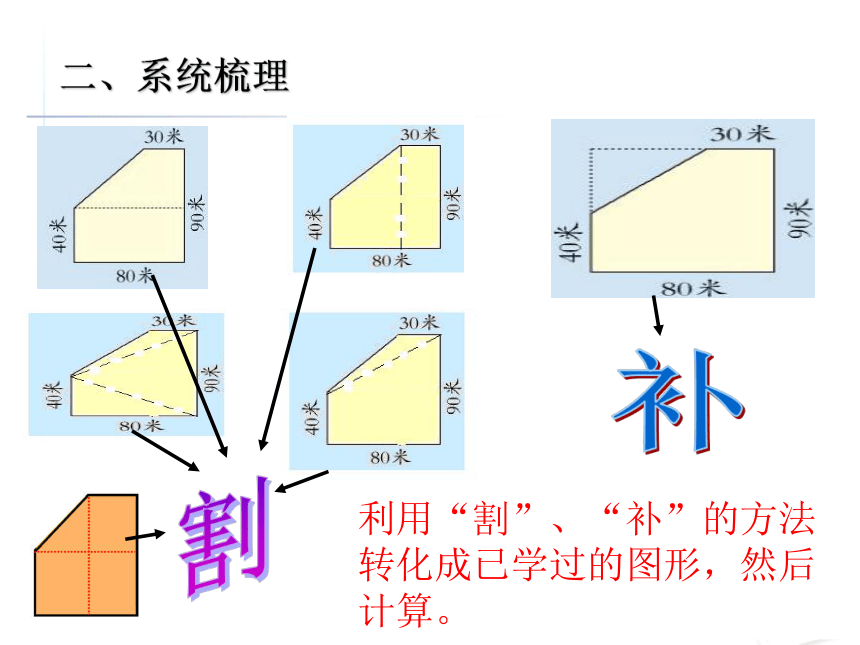
割补利用“割”、“补”的方法转化成已学过的图形,然后计算。二、系统梳理现在大家回忆一下我们是怎样来计算组合图形的面积的?用割补法计算组合图形面积时要注意:要根据图形的特点,确定是用“割”还是用“补”的方法,“割”或“补”后的图形都应是规范图形,而且“割”或“补”的平面图形越少越好,容易计算, “割”我们用加法算,“补”我们用减法计算。 二、系统梳理(1)三角形面积是平行四边形面积的一半。( ) ×三角形的面积是与它等底等高的平行四边形的面积的一半。细心判断三、基本练习(2)两个面积相等的梯形一定能拼成一个平行四边形。 ( )×三、基本练习(3)两个三角形的高相等,它们的面积就相等。 ( )×三、基本练习1.求下列图形的面积(单位cm)。三、基本练习2.2×4÷2= 8.8÷2= 4.43.8×7= 26.6(20+60)×20÷2= 80×10= 80065×50= 3250(cm2)(cm2)(cm2)(cm2)三、基本练习1432844.93543.2三、基本练习在下面的方格纸中画出一个平行四边形和一个梯形,
使它们的面积和已知三角形的面积相等。
(图中的每一个正方形边长1cm)四、综合应用解:设梯形的高为x米。
(3+7)x ÷2=20
10x ÷2x2=20x2
10x=40
10x ÷10=40 ÷10
X=4
答:梯形的高为4米。
求x的值四、综合应用2002004004000400080001.下面图形可以割补成哪些图形?你会求下面图形的面积?S组合图形 = S平行四边形+ S长方形= 480(平方厘米) 15×12 - 5×5
S组合图形 = S长方形-S正方形S组合图形 = S梯形 + S三角形= 155(平方分米)= 180 - 25 (24+36)×8÷2 + 36×30÷2 = 780(cm2)
= 60×8÷2 + 1080÷2 = 240 + 540添补法分割法分割法 30×6 +30×10 = 180 +300 四、综合应用 有一块五边形的沙发巾(如右图),制作这样一个沙发
巾需要多少平方厘米的布料?S组合图形=S长方形 + S三角形
60×40+60×40÷2 = 2400+1200 = 3600(cm2)
答:制作这样一个沙发巾需要3600平方厘米的布料?五、拓展练习S组合图形 = S梯形 – S长方形
= 54 - 6 = 48(平方米)
(8+10)×6÷2 - 3×2= 18×6÷2 - 6 答:草坪占地48平方米。五、拓展练习 小明家一面外墙墙皮脱落,要重新粉刷(如图),每平
方米需要用0.5千克涂料。如果涂料的价钱是每千克10
元,粉刷这面墙需要多少钱?= 36(平方米)
8×2÷2 + 8×3.5= 8 + 28 答:粉刷这面墙需要180元钱。S组合图形 = S三角形 + S长方形36×0.5×10 = 180(元)五、拓展练习五、拓展练习解:(4+8)×5÷2=30(平方米)
30 ×4=120(平方米)星期天,爷爷带心心到菜园散步,看到菜园旁,长着
一棵郁郁葱葱的大树。她赶忙拿起纸和笔,画了起来,
并把她估计的数据标上(如图)。她告诉爷爷,这片地的
周长约有36米,那么这片平行四边形菜地的面积有多少
平方米?解:10 ×5 =50(平方米)五、拓展练习爷爷说:“孙女考爷爷,爷爷也得考考你。来,
看爷爷画的鸡圈图:爷爷用了12米长的篱笆靠一面
墙围了一个鸡圈,你能算出这个梯形鸡圈的面积吗?8×4÷2=16(平方米)五、拓展练习12-4=8(米)老爷爷告诉你:要求梯形鸡圈的面积,可以巧妙求出梯形上下底的和是8米。答:这块地大约可种70棵樱桃树。[(25+35)×21÷2] ÷9= [60×21÷2] ÷9= 630÷9= 70(棵)五、拓展练习希望同学们从小就做一个勤于思考,乐于研究,学以致用的好孩子。
今天大家的表现都很棒,希望再接再励!很高兴与大家一起学习,下课!课后寄语这一节课中你有什么收获?还有什么疑惑? 六、回顾反思
多边形组合图形长方形正方形平行四边形三角形梯形你学过的多边形有哪些?你会求它们的面积吗?你还记得这些图形的面积计算公式吗?怎样求组合图形的面积呢?我们已经会计算哪些多边形的面积?他们的计算公式分别是什么?baS = ab aS = a2haS = ah S =(a +b)h÷2 abhahS = ah÷2 二、系统梳理这些面积计算公式是怎样推导出来的呢?长方形和正方形面积计算公式的推导。ɑbS= ab 一个正方形的面积是1平方厘米,长方形一共有b行,a列。所以长方形的面积计算公式是:S = ab。二、系统梳理 正方形是特殊的长方形,当a = b时,正方形的面积计算公式是:S = a2数方格的方法平行四边形面积计算公式的推导。 平行四边形的底就是长方形的长,高是长方形的宽,平行四边形的面积等于长方形的面积,所以平行四边形面积计算公式是:S = ah 二、系统梳理把平行四边形转化成长方形三角形面积计算公式的推导。 三角形的底就是平四边形的底,三角形的高就是平行四边形的高。二、系统梳理 两个完全相同的三角形拼成一个平行四边形。所以三角形的面积计算公式是:S = ɑh÷2 把三角形形转化成平行四边形形或学过的其他图形abhhh梯形面积计算公式的推导: 平行四边形的底就是梯形上下底之和,梯形的高就是平行四边形的高。二、系统梳理 两个梯形的面积相等,所以梯形的面积计算公式就是:
S =(ɑ+b)h÷2把梯形转化成平行四边或学过的其他图形这些图形的面积计算公式之间有着怎样的联系?二、系统梳理
割补利用“割”、“补”的方法转化成已学过的图形,然后计算。二、系统梳理现在大家回忆一下我们是怎样来计算组合图形的面积的?用割补法计算组合图形面积时要注意:要根据图形的特点,确定是用“割”还是用“补”的方法,“割”或“补”后的图形都应是规范图形,而且“割”或“补”的平面图形越少越好,容易计算, “割”我们用加法算,“补”我们用减法计算。 二、系统梳理(1)三角形面积是平行四边形面积的一半。( ) ×三角形的面积是与它等底等高的平行四边形的面积的一半。细心判断三、基本练习(2)两个面积相等的梯形一定能拼成一个平行四边形。 ( )×三、基本练习(3)两个三角形的高相等,它们的面积就相等。 ( )×三、基本练习1.求下列图形的面积(单位cm)。三、基本练习2.2×4÷2= 8.8÷2= 4.43.8×7= 26.6(20+60)×20÷2= 80×10= 80065×50= 3250(cm2)(cm2)(cm2)(cm2)三、基本练习1432844.93543.2三、基本练习在下面的方格纸中画出一个平行四边形和一个梯形,
使它们的面积和已知三角形的面积相等。
(图中的每一个正方形边长1cm)四、综合应用解:设梯形的高为x米。
(3+7)x ÷2=20
10x ÷2x2=20x2
10x=40
10x ÷10=40 ÷10
X=4
答:梯形的高为4米。
求x的值四、综合应用2002004004000400080001.下面图形可以割补成哪些图形?你会求下面图形的面积?S组合图形 = S平行四边形+ S长方形= 480(平方厘米) 15×12 - 5×5
S组合图形 = S长方形-S正方形S组合图形 = S梯形 + S三角形= 155(平方分米)= 180 - 25 (24+36)×8÷2 + 36×30÷2 = 780(cm2)
= 60×8÷2 + 1080÷2 = 240 + 540添补法分割法分割法 30×6 +30×10 = 180 +300 四、综合应用 有一块五边形的沙发巾(如右图),制作这样一个沙发
巾需要多少平方厘米的布料?S组合图形=S长方形 + S三角形
60×40+60×40÷2 = 2400+1200 = 3600(cm2)
答:制作这样一个沙发巾需要3600平方厘米的布料?五、拓展练习S组合图形 = S梯形 – S长方形
= 54 - 6 = 48(平方米)
(8+10)×6÷2 - 3×2= 18×6÷2 - 6 答:草坪占地48平方米。五、拓展练习 小明家一面外墙墙皮脱落,要重新粉刷(如图),每平
方米需要用0.5千克涂料。如果涂料的价钱是每千克10
元,粉刷这面墙需要多少钱?= 36(平方米)
8×2÷2 + 8×3.5= 8 + 28 答:粉刷这面墙需要180元钱。S组合图形 = S三角形 + S长方形36×0.5×10 = 180(元)五、拓展练习五、拓展练习解:(4+8)×5÷2=30(平方米)
30 ×4=120(平方米)星期天,爷爷带心心到菜园散步,看到菜园旁,长着
一棵郁郁葱葱的大树。她赶忙拿起纸和笔,画了起来,
并把她估计的数据标上(如图)。她告诉爷爷,这片地的
周长约有36米,那么这片平行四边形菜地的面积有多少
平方米?解:10 ×5 =50(平方米)五、拓展练习爷爷说:“孙女考爷爷,爷爷也得考考你。来,
看爷爷画的鸡圈图:爷爷用了12米长的篱笆靠一面
墙围了一个鸡圈,你能算出这个梯形鸡圈的面积吗?8×4÷2=16(平方米)五、拓展练习12-4=8(米)老爷爷告诉你:要求梯形鸡圈的面积,可以巧妙求出梯形上下底的和是8米。答:这块地大约可种70棵樱桃树。[(25+35)×21÷2] ÷9= [60×21÷2] ÷9= 630÷9= 70(棵)五、拓展练习希望同学们从小就做一个勤于思考,乐于研究,学以致用的好孩子。
今天大家的表现都很棒,希望再接再励!很高兴与大家一起学习,下课!课后寄语这一节课中你有什么收获?还有什么疑惑? 六、回顾反思
