识图析图研图一道课本习题的应用与拓展
图片预览


文档简介
课件16张PPT。识图 析图 研图一道课本习题的应用与拓展嵊州市教研室 蔡建锋(浙教版八年级上册P47第2题)
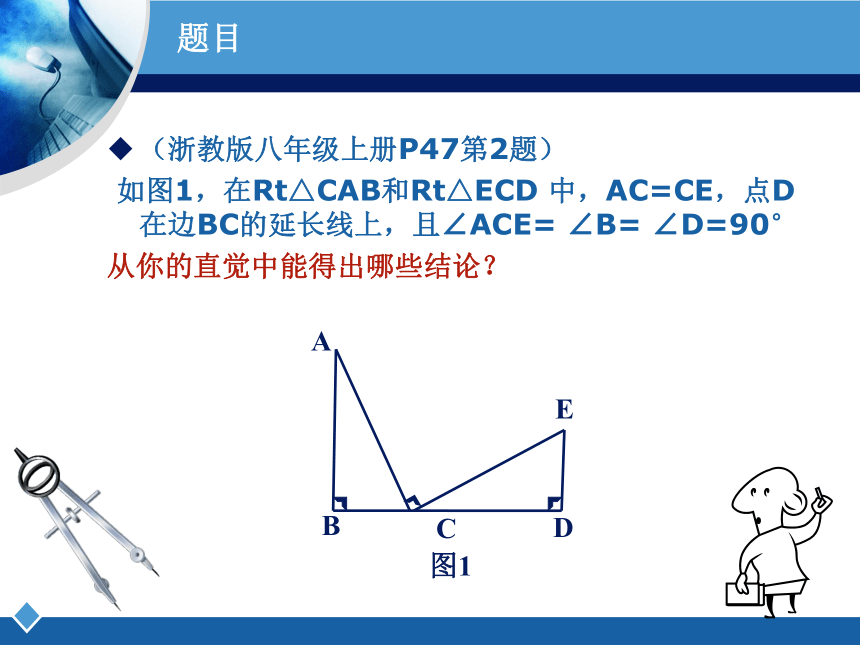
如图1,在Rt△CAB和Rt△ECD 中,AC=CE,点D在边BC的延长线上,且∠ACE= ∠B= ∠D=90°
从你的直觉中能得出哪些结论?
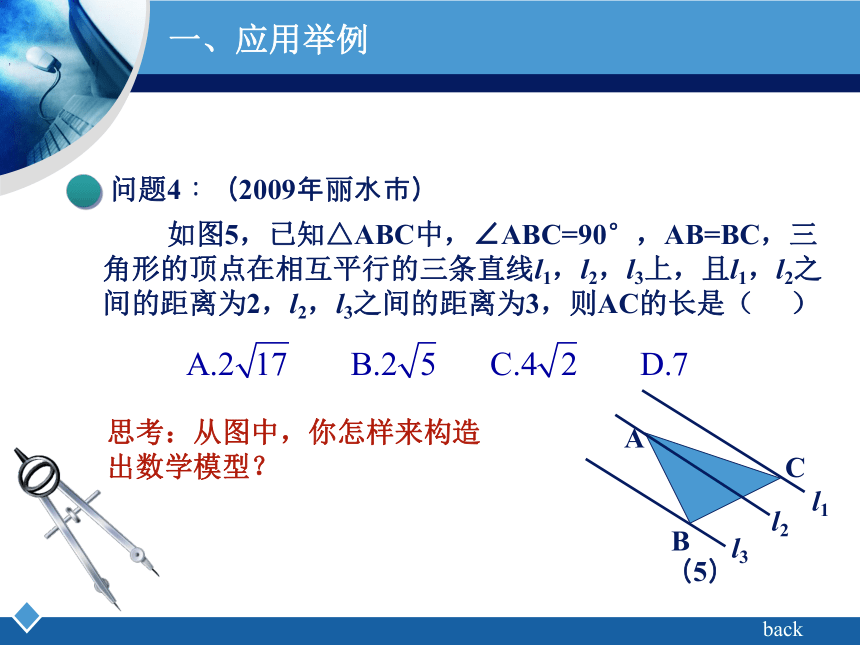
题目一、应用举例问题1问题 2问题 3问题 4一、应用举例问题1:(2008年台州市)如图2,四边形ABCD,EFGH,NHMC都是正方形,边长分别为a,b,c;A,B,N,E,F五点在同一直线上,则c = ___________(用含有a,b的代数式表示),,;back思考:你能从图中找出数学模型吗? 一、应用举例问题2:(2007年江苏南通市) 如图3,梯形ABCD中,AB∥DC,AB⊥BC,AB=
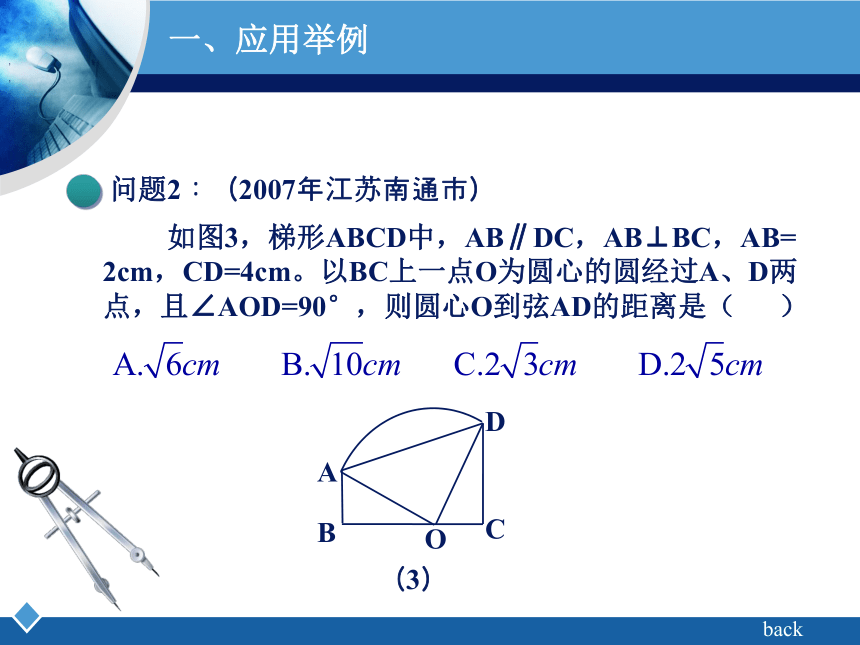
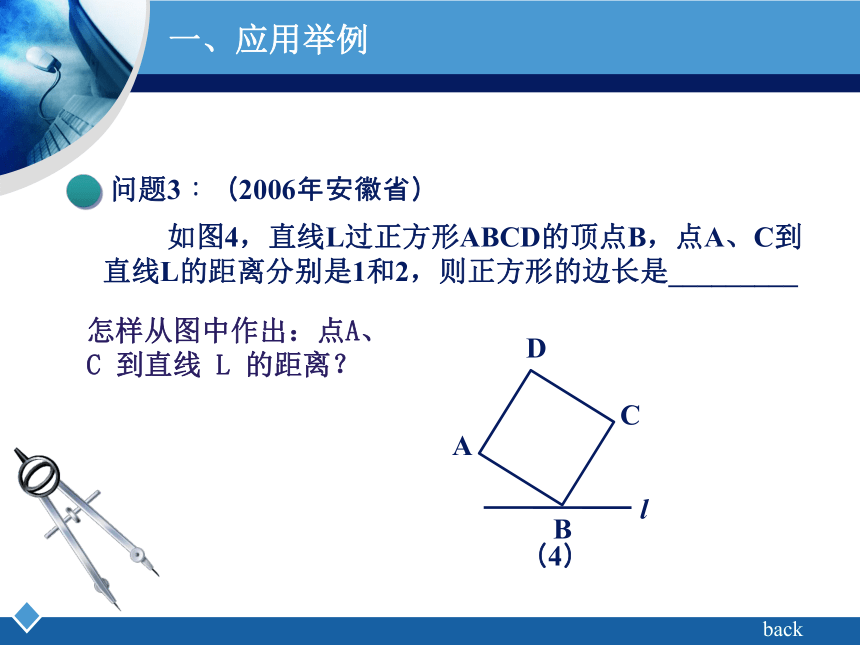
2cm,CD=4cm。以BC上一点O为圆心的圆经过A、D两点,且∠AOD=90°,则圆心O到弦AD的距离是( ),,;back一、应用举例问题3:(2006年安徽省) 如图4,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是_________;back怎样从图中作出:点A、C 到直线 L 的距离?一、应用举例问题4:(2009年丽水市) 如图5,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是( ),;back思考:从图中,你怎样来构造出数学模型? Company Logo二、拓展与应用如图6,在Rt△CAB和Rt△ECD 中, 点D在边BC的延长线上,且∠ACE= ∠B= ∠D=90°。则原题中结论还成立吗?题目变式一:(弱化条件“AC=CE(线段相等)”,则结论由三角形全等弱化为三角形相似)二、拓展与应用问题1问题2问题3二、拓展与应用问题1:(2009年长春) 如图7,在矩形ABCD中,点E、F分别在边AD、DC上, △ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长。,,;back二、拓展与应用问题2:(2009年成都市) 已知A、D是一段圆弧上的两点,且在直线l的同侧,分别过这两点作l的垂线,垂足为B、C,E是BC上一动点,连结AD、AE、DE,且∠AED=90°。
(1)如图8-1,如果AB=6,BC=16,且BE∶CE=1 ∶3,求AD的长。
(2)如图8-2,若点E恰为这段圆弧的圆心,则线段AB、BC、CD之间有怎样的等量关系?请写出你的结论并予以证明。再探究:当A、D分别在直线l两侧且AB≠CD,而其余条件不变时,线段AB、BC、CD之间又有怎样的等量关系?请直接写出结论,不必证明。,;back二、拓展与应用问题3(2008年宁波市改编)如图,长方形纸片ABCD的边长AB=8。
(1)如图9--1,把这张纸按如下步骤折叠:两次折叠
求AD的长:
(2)如图9--2,由8个大小相等的小正方形构成“”型图案,它的四个顶点分别在矩形ABCD的边上,求的长. 二、拓展与应用问题4:(2009年绍兴市) 若从矩形一边上的点到对边的视角是直角,则称该点为直角点.例如,如图的矩形ABCD中,点M在CD边上,连AM,BM,∠ABM=90°则点M为直角点.
(1)若矩形ABCD一边CD上的直角点M为中点,问该矩形的邻边具有何种数量关系?并说明理由;
(2)若点M、N分别为矩形ABCD边CD,AB上的直角点,且AB=4 ,BC= ,求MN的长. ,,;back三、综合与应用问题1:(2009年陕西省)如图,在平面直角坐标系中,OA⊥OB,且OB=2OA,点A的坐标是
(-1,2).
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中
的抛物线上求出点P,
使得△ABP与 △ABO的面积相等。三、综合与应用问题2:(2008年中考题)经过x轴上A(-1,0)B(3,0)两点的抛物线y=ax2+bx+c交y轴于点C,设抛物线的顶点为D,若以DB为直径的⊙G经过点C,求解下列问题:
(1)用含a的代数式表示出C,D两点的坐标;
(2)求抛物线的解析式;
(3)如图,当a<0时,
能否在抛物线上找到一点Q,
使△BDQ为直角三角形?
若能找到,试写出Q点的
坐标;若不能,请说明理由。Thank You !
如图1,在Rt△CAB和Rt△ECD 中,AC=CE,点D在边BC的延长线上,且∠ACE= ∠B= ∠D=90°
从你的直觉中能得出哪些结论?
题目一、应用举例问题1问题 2问题 3问题 4一、应用举例问题1:(2008年台州市)如图2,四边形ABCD,EFGH,NHMC都是正方形,边长分别为a,b,c;A,B,N,E,F五点在同一直线上,则c = ___________(用含有a,b的代数式表示),,;back思考:你能从图中找出数学模型吗? 一、应用举例问题2:(2007年江苏南通市) 如图3,梯形ABCD中,AB∥DC,AB⊥BC,AB=
2cm,CD=4cm。以BC上一点O为圆心的圆经过A、D两点,且∠AOD=90°,则圆心O到弦AD的距离是( ),,;back一、应用举例问题3:(2006年安徽省) 如图4,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是_________;back怎样从图中作出:点A、C 到直线 L 的距离?一、应用举例问题4:(2009年丽水市) 如图5,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是( ),;back思考:从图中,你怎样来构造出数学模型? Company Logo二、拓展与应用如图6,在Rt△CAB和Rt△ECD 中, 点D在边BC的延长线上,且∠ACE= ∠B= ∠D=90°。则原题中结论还成立吗?题目变式一:(弱化条件“AC=CE(线段相等)”,则结论由三角形全等弱化为三角形相似)二、拓展与应用问题1问题2问题3二、拓展与应用问题1:(2009年长春) 如图7,在矩形ABCD中,点E、F分别在边AD、DC上, △ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长。,,;back二、拓展与应用问题2:(2009年成都市) 已知A、D是一段圆弧上的两点,且在直线l的同侧,分别过这两点作l的垂线,垂足为B、C,E是BC上一动点,连结AD、AE、DE,且∠AED=90°。
(1)如图8-1,如果AB=6,BC=16,且BE∶CE=1 ∶3,求AD的长。
(2)如图8-2,若点E恰为这段圆弧的圆心,则线段AB、BC、CD之间有怎样的等量关系?请写出你的结论并予以证明。再探究:当A、D分别在直线l两侧且AB≠CD,而其余条件不变时,线段AB、BC、CD之间又有怎样的等量关系?请直接写出结论,不必证明。,;back二、拓展与应用问题3(2008年宁波市改编)如图,长方形纸片ABCD的边长AB=8。
(1)如图9--1,把这张纸按如下步骤折叠:两次折叠
求AD的长:
(2)如图9--2,由8个大小相等的小正方形构成“”型图案,它的四个顶点分别在矩形ABCD的边上,求的长. 二、拓展与应用问题4:(2009年绍兴市) 若从矩形一边上的点到对边的视角是直角,则称该点为直角点.例如,如图的矩形ABCD中,点M在CD边上,连AM,BM,∠ABM=90°则点M为直角点.
(1)若矩形ABCD一边CD上的直角点M为中点,问该矩形的邻边具有何种数量关系?并说明理由;
(2)若点M、N分别为矩形ABCD边CD,AB上的直角点,且AB=4 ,BC= ,求MN的长. ,,;back三、综合与应用问题1:(2009年陕西省)如图,在平面直角坐标系中,OA⊥OB,且OB=2OA,点A的坐标是
(-1,2).
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中
的抛物线上求出点P,
使得△ABP与 △ABO的面积相等。三、综合与应用问题2:(2008年中考题)经过x轴上A(-1,0)B(3,0)两点的抛物线y=ax2+bx+c交y轴于点C,设抛物线的顶点为D,若以DB为直径的⊙G经过点C,求解下列问题:
(1)用含a的代数式表示出C,D两点的坐标;
(2)求抛物线的解析式;
(3)如图,当a<0时,
能否在抛物线上找到一点Q,
使△BDQ为直角三角形?
若能找到,试写出Q点的
坐标;若不能,请说明理由。Thank You !
同课章节目录
