沪科版八年级数学上13.1.2三角形中角的关系教案
文档属性
| 名称 | 沪科版八年级数学上13.1.2三角形中角的关系教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 17.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-25 07:06:19 | ||
图片预览

文档简介
2.三角形中角的关系
教学目标
知识与技能
1、了解三角形的内角;2、会用平行线的性质与平角的定义证明三角形内角和等于180度;3、学会解决与求角有关的实际问题;
过程与方法
经历实验活动的过程,掌握三角形的内角和定理,初步掌握添加辅助线的方法.
情感态度价值观
初步培养学生的说理能力。
教学重点
三角形的内角和定理及其运用
教学难点
三角形内角和定理的推理过程
教学准备
三角尺、小剪刀、量角器。
教学过程(师生活动)
设计理念
动手操作初步感知
我们都知道,任意一个三角形的内角和都等于180°,怎么说明这个结论的正确性呢?
在纸上画一个三角形将将它的内角剪下,试着拼拼看。
情境教学对激发学生的学习兴趣有很大的作用。
实践说理深入新知
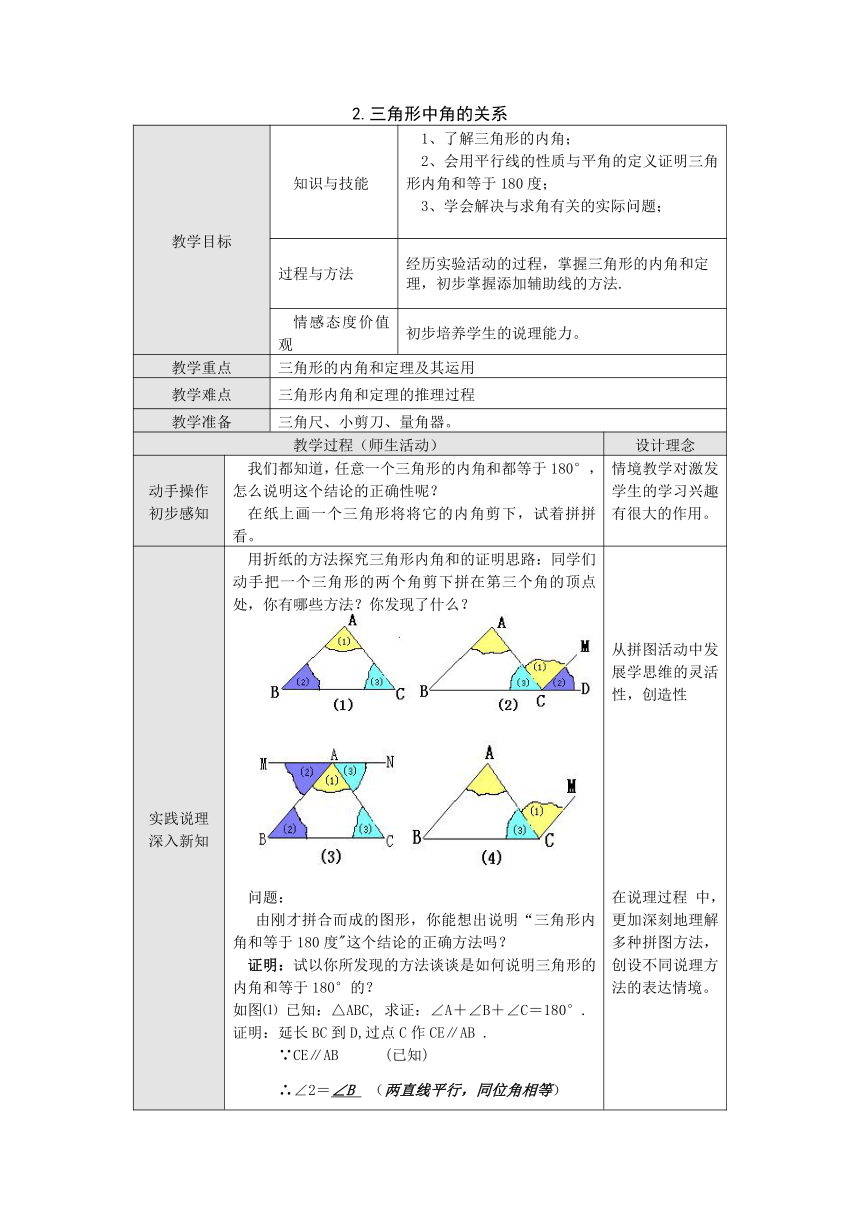
用折纸的方法探究三角形内角和的证明思路:同学们动手把一个三角形的两个角剪下拼在第三个角的顶点处,你有哪些方法?你发现了什么?问题:
由刚才拼合而成的图形,你能想出说明“三角形内角和等于180度"这个结论的正确方法吗?
证明:试以你所发现的方法谈谈是如何说明三角形的内角和等于180°的?如图⑴
已知:△ABC,
求证:∠A+∠B+∠C=180°.证明:延长BC到D,过点C作CE∥AB
.
∵CE∥AB
(已知)
∴∠2=∠B
(两直线平行,同位角相等)∠1=∠A
(两直线平行,内错角相等)
又∵∠1+∠2+∠3=180°
(平角定义)
∴∠A+∠B+∠ACB=180°(等量代换)三角形内角和定理:三角形的内角和等于180°
从拼图活动中发展学思维的灵活性,创造性在说理过程
中,更加深刻地理解多种拼图方法,创设不同说理方法的表达情境。
应用新知
1、如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C
岛在B
岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度 分析:虽然本题已给图形,但我们必须从画图入手,
记住画图的过程就是理解题目的开始,C岛在A岛的北偏东50°方向,就是以A岛为中心画方向线AC,B岛在A
岛的北偏东80°,也是以岛为中心画方向线AB,C岛在B岛的北偏西40°方向,这就是以B
岛为中心画出方向线BC、AC与BC交于C.
由于A、B、C三点构成△ABC.
所求∠ACB是△ABC的一个内角,这样就要懂得∠CAB和∠ABC的度数.
根据方向线不难得到∠CAB=80°-50°=30°,
由BF∥AE得∠FBA=100°,即∠CBA=60°,
解:(略)
向学生展示分析问题的基本方法,培养学生思维的广阔性。
课堂练习
1.完成课本练习.2.已知△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数。
巩固了前面的已学知识,进一步提高学生的说理能力。
小结与作业
课堂小结
采用让学生归纳、补充,然后教师补充的方式进行。1.本节课我们学了什么知识?2.你有什么收获?
发挥学生主体意识,培养学生语言概括能力。
本课作业
必做题:
选做题:
作业分层,供不同层次的学生使用
教学目标
知识与技能
1、了解三角形的内角;2、会用平行线的性质与平角的定义证明三角形内角和等于180度;3、学会解决与求角有关的实际问题;
过程与方法
经历实验活动的过程,掌握三角形的内角和定理,初步掌握添加辅助线的方法.
情感态度价值观
初步培养学生的说理能力。
教学重点
三角形的内角和定理及其运用
教学难点
三角形内角和定理的推理过程
教学准备
三角尺、小剪刀、量角器。
教学过程(师生活动)
设计理念
动手操作初步感知
我们都知道,任意一个三角形的内角和都等于180°,怎么说明这个结论的正确性呢?
在纸上画一个三角形将将它的内角剪下,试着拼拼看。
情境教学对激发学生的学习兴趣有很大的作用。
实践说理深入新知
用折纸的方法探究三角形内角和的证明思路:同学们动手把一个三角形的两个角剪下拼在第三个角的顶点处,你有哪些方法?你发现了什么?问题:
由刚才拼合而成的图形,你能想出说明“三角形内角和等于180度"这个结论的正确方法吗?
证明:试以你所发现的方法谈谈是如何说明三角形的内角和等于180°的?如图⑴
已知:△ABC,
求证:∠A+∠B+∠C=180°.证明:延长BC到D,过点C作CE∥AB
.
∵CE∥AB
(已知)
∴∠2=∠B
(两直线平行,同位角相等)∠1=∠A
(两直线平行,内错角相等)
又∵∠1+∠2+∠3=180°
(平角定义)
∴∠A+∠B+∠ACB=180°(等量代换)三角形内角和定理:三角形的内角和等于180°
从拼图活动中发展学思维的灵活性,创造性在说理过程
中,更加深刻地理解多种拼图方法,创设不同说理方法的表达情境。
应用新知
1、如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C
岛在B
岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度 分析:虽然本题已给图形,但我们必须从画图入手,
记住画图的过程就是理解题目的开始,C岛在A岛的北偏东50°方向,就是以A岛为中心画方向线AC,B岛在A
岛的北偏东80°,也是以岛为中心画方向线AB,C岛在B岛的北偏西40°方向,这就是以B
岛为中心画出方向线BC、AC与BC交于C.
由于A、B、C三点构成△ABC.
所求∠ACB是△ABC的一个内角,这样就要懂得∠CAB和∠ABC的度数.
根据方向线不难得到∠CAB=80°-50°=30°,
由BF∥AE得∠FBA=100°,即∠CBA=60°,
解:(略)
向学生展示分析问题的基本方法,培养学生思维的广阔性。
课堂练习
1.完成课本练习.2.已知△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数。
巩固了前面的已学知识,进一步提高学生的说理能力。
小结与作业
课堂小结
采用让学生归纳、补充,然后教师补充的方式进行。1.本节课我们学了什么知识?2.你有什么收获?
发挥学生主体意识,培养学生语言概括能力。
本课作业
必做题:
选做题:
作业分层,供不同层次的学生使用
