湖南省衡阳县江山学校2015-2016学年高一下学期第一阶段考试数学试卷
文档属性
| 名称 | 湖南省衡阳县江山学校2015-2016学年高一下学期第一阶段考试数学试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 227.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-26 00:00:00 | ||
图片预览




文档简介
欢迎广大教师踊跃来稿,稿酬丰厚,qq:2355394557
欢迎广大教师踊跃来稿,稿酬丰厚,qq:2355394557
广丰一中2015-2016学年高一第二学期课改实验班
第一次阶段性考试数学试卷
一、选择题(本大题共12小题,每小题5分,共60分)
1.已知集合,,则(
)
A.
B.
C.
D.
2.下列说法中正确的是(
)
A.三点确定一个平面。B.两条直线确定一个平面。C.两两相交的三条直线一定在同一平面内。D.过同一点的三条直线不一定在同一平面内。
3.某空间几何体的三视图中,有一个是正方形,则该空间几何体不可能是(
)
A.圆柱
B.圆锥
C.棱锥
D.棱柱
4.关于斜二测画法画直观图说法不正确的是(
).
A.在实物图中取坐标系不同,所得的直观图有可能不同。
B.平行于坐标轴的线段在直观图中仍然平行于坐标轴。
C.平行于坐标轴的线段长度在直观图中仍然保持不变。
D.斜二测坐标系取的角可能是135°。
5.函数的零点所在的一个区间是(
)
A.
B.
C.
D.
6.若是定义在上的偶函数,有,则(
)
A.
B.
C.
D.
7.已知函数f(+1)=x+1,则函数f(x)的解析式为(
)
A.f(x)=x2
B.f(x)
=x2+1(x≥1)
C.f(x)=x2-2x+2
(x≥1)
D.f(x)=x2-2x(x≥1)
8.幂函数在为减函数,则的值为(
)
A.1
或3
B.1
C.3
D.2
9.已知函数当时,,则此函数的单调递减区间为(
)
A.
B.
C.
D.
10.若函数是上的增函数,则实数的范围为(
)
A.
B.
C.
D.
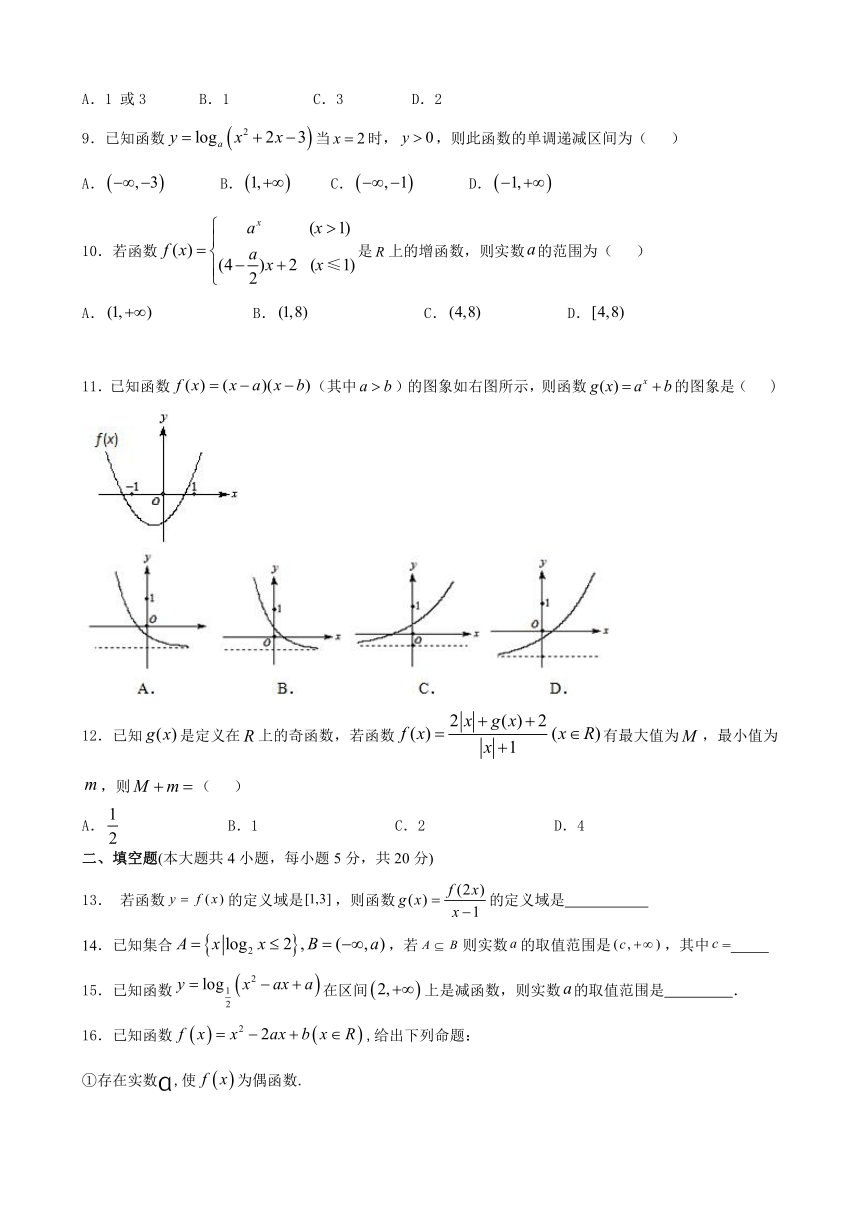
11.已知函数(其中)的图象如右图所示,则函数的图象是(
)
12.已知是定义在上的奇函数,若函数有最大值为,最小值为,则(
)
A.
B.1
C.2
D.4
二、填空题(本大题共4小题,每小题5分,共20分)
13.
若函数的定义域是,则函数的定义域是
14.已知集合,若则实数的取值范围是,其中=
15.已知函数在区间上是减函数,则实数的取值范围是
.
16.已知函数,给出下列命题:
①存在实数ɑ,使为偶函数.
②若,则
的图像关于对称.
③若,则在区间上是增函数
④若,则函数有个零点.
其中正确命题的序号为
.
三、解答题(17题10分,其余每题12分,共70分)
17.(本题满分10分)如图,E、F、G、H分别是空间四边形AB、BC、CD、DA上的点,
且EH与FG交于点O.求证:B、D、O三点共线.
18(本题满分12分)已知集合,
(1)求;
(2)若集合且,求的取值范围。
19.(本题满分12分)已知函数的图象恒过定点,且点又在函数的图象上。
(1)求实数的值
(2)解不等式
20.(本题满分12分)已知函数.
(1)当时,求函数在上的值域;
(2)若对任意,总有成立,求实数的取值范围.
21.(本题满分12分)已知二次函数满足且
(1)求二次函数的解析式.
(2)求函数的单调增区间和值域
.
22(本题满分12分).已知函数是定义在的奇函数,且
(1)求解析式.(2)用定义证明在上是增函数。
(3)解不等式。
第一次阶段性考试数学答题卷
.姓名
班级
学号
一、选择题(5×12=60)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(4×5=20)
13、
14、
15、
16、
三、解答题(17题10分,其余每题12分,共70分)
17.(本题满分10分)如图,E、F、G、H分别是空间四边形AB、BC、CD、DA上的点,
且EH与FG交于点O.求证:B、D、O三点共线.
18.(本题满分12分)已知集合,
(1)求;
(2)若集合且,求的取值范围。
19.(本题满分12分)已知函数的图象恒过定点,且点又在函数的图象上。
(1)求实数的值
。
(2)解不等式
20.(本题满分12分)已知函数.
(1)当时,求函数在上的值域;
(2)若对任意,总有成立,求实数的取值范围.
21.(本题满分12分)已知二次函数满足且
(1)求二次函数的解析式.
(2)求函数的单调增区间和值域
.
22.(本题满分12分)已知函数是定义在的奇函数,且
(1)求解析式
(2)用定义证明在上是增函数
(3)解不等式
参考答案
选择题
1-12:BDBCD
DCCAD
AD
二.填空题
13.【答案】
14.【答案】4
15.【答案】
16.
【答案】①②③
三、解答题(17题10分,其余每题12分,共70分)
17.如图,E、F、G、H分别是空间四边形AB、BC、CD、DA上的点,
且EH与FG交于点O.求证:B、D、O三点共线.
解:
∵E∈AB,H∈AD,
∴E∈平面ABD,H∈平面ABD.
∴EH平面ABD.
∵EH∩FG=O,∴O∈平面ABD.--------4分
同理可证O∈平面BCD,--------------7分
∴O∈平面ABD∩平面BCD,即O∈BD,
所以B、D、O三点共线.------------10分
18.已知集合,
(1)求;
(2)若集合且,求的取值范围。
【答案】
(1);(2)
19.已知函数的图象恒过定点,且点又在函数的图象上。
(1)求实数的值
(2)解不等式
【答案】(1)2
(2)见解析
20.已知函数.
(1)当时,求函数在上的值域;
(2)若对任意,总有成立,求实数的取值范围.
【答案】(1);(2).
21.(本题满分12分)已知二次函数满足且
(1)求二次函数的解析式.
(2)求函数的单调增区间和值域
.
【答案】(1)f(x)=2x2-2x+1;(2)单调增区间为,函数的值域为
22.已知函数是定义在的奇函数,且
(1)求解析式
(2)用定义证明在上是增函数
(3)解不等式
【答案】
(1);(2)略;(3)
浙江、福建、安徽、江西、广东、广西、海南
资源投稿
qq:2355394557
浙江、福建、安徽、江西、广东、广西、海南
资源投稿
qq:2355394557
欢迎广大教师踊跃来稿,稿酬丰厚,qq:2355394557
广丰一中2015-2016学年高一第二学期课改实验班
第一次阶段性考试数学试卷
一、选择题(本大题共12小题,每小题5分,共60分)
1.已知集合,,则(
)
A.
B.
C.
D.
2.下列说法中正确的是(
)
A.三点确定一个平面。B.两条直线确定一个平面。C.两两相交的三条直线一定在同一平面内。D.过同一点的三条直线不一定在同一平面内。
3.某空间几何体的三视图中,有一个是正方形,则该空间几何体不可能是(
)
A.圆柱
B.圆锥
C.棱锥
D.棱柱
4.关于斜二测画法画直观图说法不正确的是(
).
A.在实物图中取坐标系不同,所得的直观图有可能不同。
B.平行于坐标轴的线段在直观图中仍然平行于坐标轴。
C.平行于坐标轴的线段长度在直观图中仍然保持不变。
D.斜二测坐标系取的角可能是135°。
5.函数的零点所在的一个区间是(
)
A.
B.
C.
D.
6.若是定义在上的偶函数,有,则(
)
A.
B.
C.
D.
7.已知函数f(+1)=x+1,则函数f(x)的解析式为(
)
A.f(x)=x2
B.f(x)
=x2+1(x≥1)
C.f(x)=x2-2x+2
(x≥1)
D.f(x)=x2-2x(x≥1)
8.幂函数在为减函数,则的值为(
)
A.1
或3
B.1
C.3
D.2
9.已知函数当时,,则此函数的单调递减区间为(
)
A.
B.
C.
D.
10.若函数是上的增函数,则实数的范围为(
)
A.
B.
C.
D.
11.已知函数(其中)的图象如右图所示,则函数的图象是(
)
12.已知是定义在上的奇函数,若函数有最大值为,最小值为,则(
)
A.
B.1
C.2
D.4
二、填空题(本大题共4小题,每小题5分,共20分)
13.
若函数的定义域是,则函数的定义域是
14.已知集合,若则实数的取值范围是,其中=
15.已知函数在区间上是减函数,则实数的取值范围是
.
16.已知函数,给出下列命题:
①存在实数ɑ,使为偶函数.
②若,则
的图像关于对称.
③若,则在区间上是增函数
④若,则函数有个零点.
其中正确命题的序号为
.
三、解答题(17题10分,其余每题12分,共70分)
17.(本题满分10分)如图,E、F、G、H分别是空间四边形AB、BC、CD、DA上的点,
且EH与FG交于点O.求证:B、D、O三点共线.
18(本题满分12分)已知集合,
(1)求;
(2)若集合且,求的取值范围。
19.(本题满分12分)已知函数的图象恒过定点,且点又在函数的图象上。
(1)求实数的值
(2)解不等式
20.(本题满分12分)已知函数.
(1)当时,求函数在上的值域;
(2)若对任意,总有成立,求实数的取值范围.
21.(本题满分12分)已知二次函数满足且
(1)求二次函数的解析式.
(2)求函数的单调增区间和值域
.
22(本题满分12分).已知函数是定义在的奇函数,且
(1)求解析式.(2)用定义证明在上是增函数。
(3)解不等式。
第一次阶段性考试数学答题卷
.姓名
班级
学号
一、选择题(5×12=60)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(4×5=20)
13、
14、
15、
16、
三、解答题(17题10分,其余每题12分,共70分)
17.(本题满分10分)如图,E、F、G、H分别是空间四边形AB、BC、CD、DA上的点,
且EH与FG交于点O.求证:B、D、O三点共线.
18.(本题满分12分)已知集合,
(1)求;
(2)若集合且,求的取值范围。
19.(本题满分12分)已知函数的图象恒过定点,且点又在函数的图象上。
(1)求实数的值
。
(2)解不等式
20.(本题满分12分)已知函数.
(1)当时,求函数在上的值域;
(2)若对任意,总有成立,求实数的取值范围.
21.(本题满分12分)已知二次函数满足且
(1)求二次函数的解析式.
(2)求函数的单调增区间和值域
.
22.(本题满分12分)已知函数是定义在的奇函数,且
(1)求解析式
(2)用定义证明在上是增函数
(3)解不等式
参考答案
选择题
1-12:BDBCD
DCCAD
AD
二.填空题
13.【答案】
14.【答案】4
15.【答案】
16.
【答案】①②③
三、解答题(17题10分,其余每题12分,共70分)
17.如图,E、F、G、H分别是空间四边形AB、BC、CD、DA上的点,
且EH与FG交于点O.求证:B、D、O三点共线.
解:
∵E∈AB,H∈AD,
∴E∈平面ABD,H∈平面ABD.
∴EH平面ABD.
∵EH∩FG=O,∴O∈平面ABD.--------4分
同理可证O∈平面BCD,--------------7分
∴O∈平面ABD∩平面BCD,即O∈BD,
所以B、D、O三点共线.------------10分
18.已知集合,
(1)求;
(2)若集合且,求的取值范围。
【答案】
(1);(2)
19.已知函数的图象恒过定点,且点又在函数的图象上。
(1)求实数的值
(2)解不等式
【答案】(1)2
(2)见解析
20.已知函数.
(1)当时,求函数在上的值域;
(2)若对任意,总有成立,求实数的取值范围.
【答案】(1);(2).
21.(本题满分12分)已知二次函数满足且
(1)求二次函数的解析式.
(2)求函数的单调增区间和值域
.
【答案】(1)f(x)=2x2-2x+1;(2)单调增区间为,函数的值域为
22.已知函数是定义在的奇函数,且
(1)求解析式
(2)用定义证明在上是增函数
(3)解不等式
【答案】
(1);(2)略;(3)
浙江、福建、安徽、江西、广东、广西、海南
资源投稿
qq:2355394557
浙江、福建、安徽、江西、广东、广西、海南
资源投稿
qq:2355394557
同课章节目录
