抛物线的定义课件

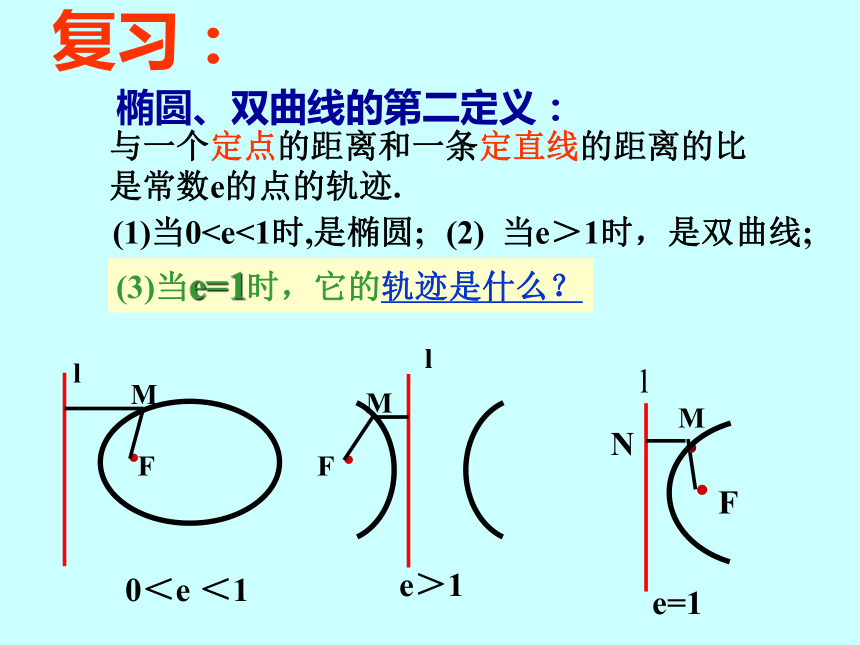
课件20张PPT。抛物线及其标准方程复习：椭圆、双曲线的第二定义：与一个定点的距离和一条定直线的距离的比
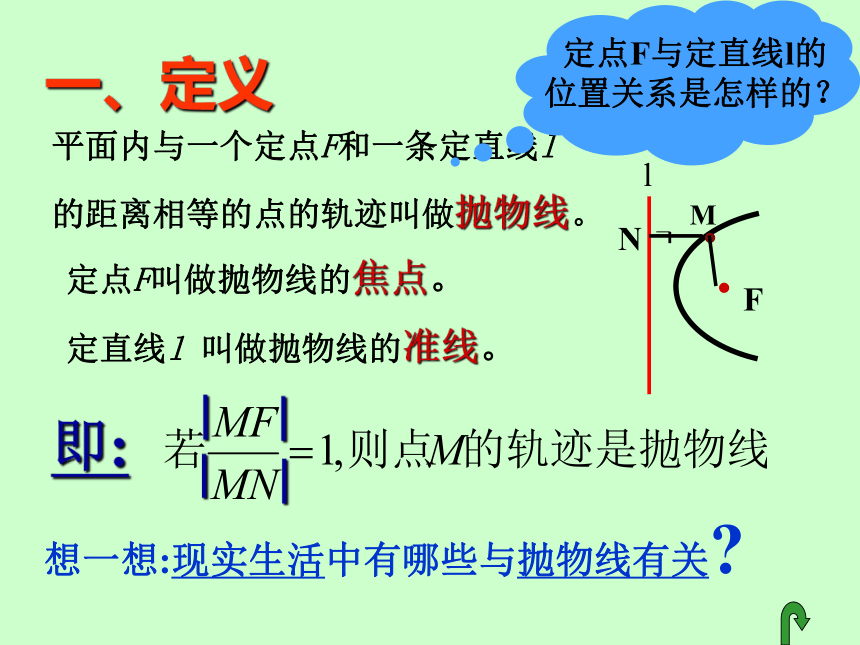
是常数e的点的轨迹.(2) 当e＞1时，是双曲线;(3)当e=1时，它的轨迹是什么？(1)当0的距离相等的点的轨迹叫做抛物线。一、定义想一想:现实生活中有哪些与抛物线有关?定点F叫做抛物线的焦点。
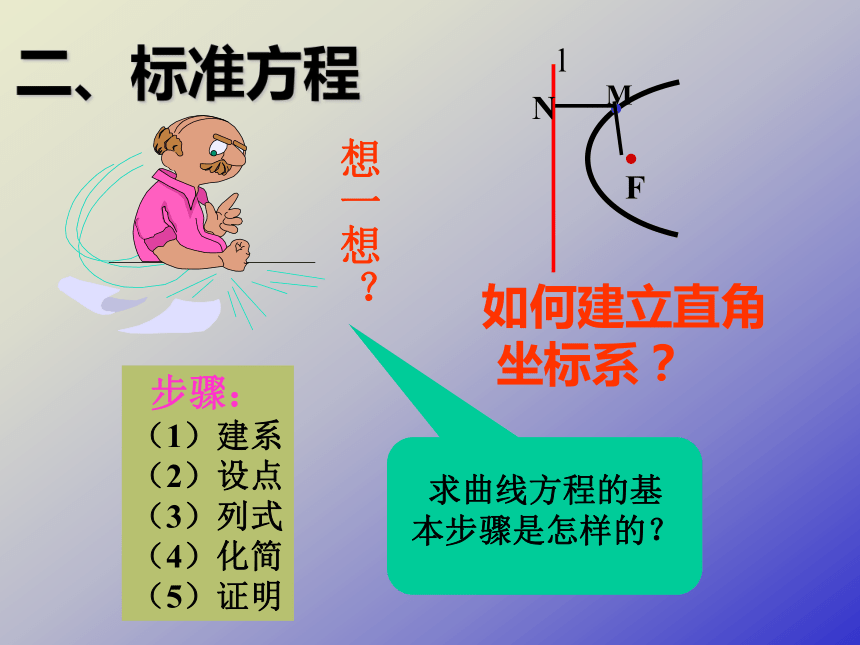
定直线l 叫做抛物线的准线。二、标准方程如何建立直角
坐标系？想一想？步骤：（1）建系（2）设点（3）列式（4）化简（5）证明二、标准方程K设︱KF︱= p设点M的坐标为（x，y）， 由定义可知，取过焦点F且垂直于准线l的直线为x轴，线段KF的中垂线y轴 方程 y2 = 2px（p＞0）叫做抛物线的标准方程其中 p 为正常数，它的几何意义是: 焦 点 到 准 线 的 距 离§8.7 抛物线及其标准方程一.定义:平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线。定点F叫做抛物线的焦点定直线l 叫做抛物线的准线。 二.标准方程: 一条抛物线，由于它在坐标平面内的位置不同，方程也不同，所以抛物线的标准方程还有其它形式.方程y2 = 2px（p＞0）表示抛物线的焦点在 X轴的正半轴上 椭圆，双曲线，抛物线各有几条准线？ 根据上表中抛物线的标准方程的不同形式与图形、焦点坐标、准线方程对应关系，如何判断抛物线的焦点位置，开口方向？想一想:第一：一次项的变量如为X（或Y） 则X轴（或Y轴）为抛物线的对称轴，焦点就在对称轴上。！
第二：一次的系数决定了开口方向 例1（1）已知抛物线的标准方程是y2 = 6x，
求它的焦点坐标和准线方程；（2）已知抛物线的方程是y = －6x2，
求它的焦点坐标和准线方程；（3）已知抛物线的焦点坐标是F（0，-2），
求它的标准方程。 1 12例2、求过点A（-3，2）的抛物线的
标准方程。解：当抛物线的焦点在y轴
的正半轴上时，把A（-3，2）
代入x2 =2py，得p= 当焦点在x轴的负半轴上时，
把A（-3，2）代入y2 = -2px，
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
思考题、M是抛物线y2 = 2px（P＞0）上一点，若点
M 的横坐标为X0，则点M到焦点的距离是


————————————练习：1、根据下列条件，写出抛物线的标准方程：（1）焦点是F（3，0）；（2）准线方程 是x = ；（3）焦点到准线的距离是2。y2 =12xy2 =xy2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y2、求下列抛物线的焦点坐标和准线方程：
（1）y2 = 20x （2）x2= y （3）x2 +8y =0（5，0）x= -5y=2(0 , -2)小 结 ：1、抛物线的定义,标准方程类型与图象的对应
关系以及判断方法2、抛物线的定义、标准方程和它
的焦点、准线、方程3、求标准方程（1）用定义；
（2）用待定系数法
课堂作业：课本 P119： 3、4、6同学们，再见！