9.3 平行四边形 教学设计

平行四边形
教学目标：
知道平行四边形的概念及其性质.
能够利用平行四边形的概念及其性质解决有关问题.
经历观察、操作、发现、探究平行四边形的基本性质的过程，发展学生的观察能力和动手操作能力.
在与他人的合作交流等活动过程中，发展合情推理的能力和有条理地思考和表达的能力.
教学重点：
平行四边形的概念及其性质，能够利用平行四边形的概念及其性质解决有关问题.
教学难点：
灵活利用平行四边形的概念及其性质解决有关问题.
一、创设情境，引入课题
利用课件展示几幅有关平行四边形的图片，以此引入，观察，探索：图片中有你熟悉的图形吗？
(设计意图：利用几组平行四边形图片的播放，引导学生感受到生活中处处有数学，感受到平行四边形就在身边，体会到数学的生活化)
二、引导探索，归纳概念
活动一 探索平行四边形的概念
1.操作：BO是△ABC边AC上的中线，画出△ABC关于点O的对称的图形.
(设计意图：让学生在实际操作中加深对中心对称图形的理解，充分发挥学生的主体地位)
2．提问：这个四边形是中心对称图形吗？若是，则对称中心是什么？
△ 可以看做是△ABC绕点 旋转 0得到的，因此四边形ABCD是 ，点 是它的 .
3．讨论：图中的AB与CD，AD与CB平行吗？为什么？
概念：两组对边分别平行的四边形叫做平行四边形.记作 ，读作 .
平行四边形是 图形， 是它的对称中心.
4.概念再认识：概念既是判别图形的条件，又是图形的性质.
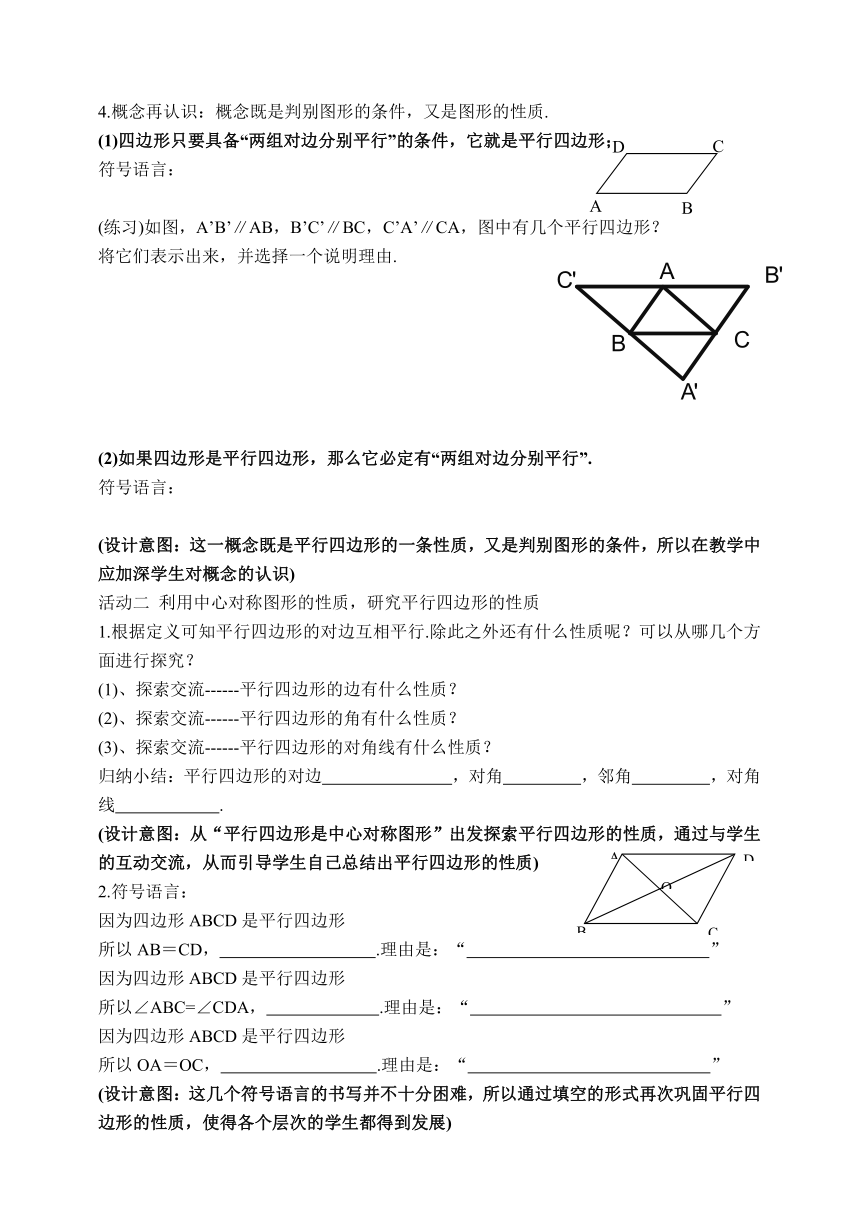
(1)四边形只要具备“两组对边分别平行”的条件，它就是平行四边形；
符号语言：
(练习)如图，A’B’∥AB，B’C’∥BC，C’A’∥CA，图中有几个平行四边形？
将它们表示出来，并选择一个说明理由.
(2)如果四边形是平行四边形，那么它必定有“两组对边分别平行”.
符号语言：
(设计意图：这一概念既是平行四边形的一条性质，又是判别图形的条件，所以在教学中应加深学生对概念的认识)
活动二 利用中心对称图形的性质，研究平行四边形的性质
1.根据定义可知平行四边形的对边互相平行.除此之外还有什么性质呢？可以从哪几个方面进行探究？
(1)、探索交流------平行四边形的边有什么性质？
(2)、探索交流------平行四边形的角有什么性质？
(3)、探索交流------平行四边形的对角线有什么性质？
归纳小结：平行四边形的对边 ，对角 ，邻角 ，对角线 .
(设计意图：从“平行四边形是中心对称图形”出发探索平行四边形的性质，通过与学生的互动交流，从而引导学生自己总结出平行四边形的性质)
2.符号语言：
因为四边形ABCD是平行四边形
所以AB＝CD， .理由是：“ ”
因为四边形ABCD是平行四边形
所以∠ABC=∠CDA， .理由是：“ ”
因为四边形ABCD是平行四边形
所以OA＝OC， .理由是：“ ”
(设计意图：这几个符号语言的书写并不十分困难，所以通过填空的形式再次巩固平行四边形的性质，使得各个层次的学生都得到发展)
三、巩固概念，应用拓展
1、在□ABCD中，AB=8,BC=4,CD= ，AD= ，□ABCD的周长= .
2、在□ABCD中，∠B=50°，∠A= ，∠C= ，∠D= .
变式：如图，在□ABCD中，如果∠B+∠D=1000，那么平行四边形的每个内角是多少度？
3、如图，□ABCD的对角线相交于点O，BC＝7cm，BD＝10cm，AC＝6cm，你还能知道什么？
(设计意图：通过练习及变式，再次巩固平行四边形的性质，养成良好的思维习惯)
四、自主小结，系统归纳
1、平行四边形的概念： ；
概念既是 ，又是 .
2、平行四边形的性质：
平行四边形
性质
对称性
对边
对角
邻角
对角线
(设计意图：通过学生的自主小结，再次加深学生对平行四边形的定义及性质的掌握，使知识系统化)
五、布置作业，继续探究
1、下列性质中，平行四边形不一定具备的是( )
(A)对角互补 (B)邻角互补 (C)对角相等 (D)对边相等
2、如图，在□ABCD中，AC与BD相交于点O，则图中全等三角形有( )
(A)1对 (B)2对 (C)3对 (D)4对
3、□ABCD中，∠A：∠B：∠C：∠D的值可以是( )
(A)1:2:3:4 (B)2:2:3:3 (C)2:3:3:2 (D)2:3:2:3
4、在□ABCD中，∠A、∠B的平分线交于E，则∠AEB是( )
(A)直角 (B)钝角 (C)锐角 (D)无法确定
5、以不在同一直线上的三点A、B、C为其中的三个顶点作不同的平行四边形，一共可以作( )
(A)1个 (B)2个 (C)3个 (D)4个
6、平行四边形的一边等于14，它的对角线可能的取值是( )
(A)8cm和16cm (B) 10cm和16cm (C) 12cm和16cm (D) 20cm和22cm
7、(1)已知：□ABCD中，∠B=60°，∠A= , ∠C= , ∠D= .
(2)已知：□ABCD中，∠A：∠B =3:1，∠A= , ∠B= ，∠C= , ∠D= .
(3)已知：□ABCD中，∠A比∠B大 200，∠A= , ∠B= ,∠C= , ∠D= .
(4)已知：□ABCD中，∠A+∠C=200°，∠A= , ∠B= ,∠C= , ∠D= .
8、(1)如图，已知□ABCD中，AB=4,BC=6，则AD＝ ，CD＝ .
(2)□ABCD的周长是20，已知AB＝4，则BC＝ ，CD＝ .
(3)□ABCD的周长是20，AB ：CB=2：3，则AD= ，CD= .
9、如图，□ABCD的面积为40,DE⊥AB，DF⊥BC，且DE=4，DF=5.求这个平行四边形的周长.
变式：如图，□ABCD的周长为36 ,DE⊥AB，DF⊥BC，且DE=4，DF=5.求这个平行四边形的面积.
教后反思
《平行四边形》这节课承接了上一节旋转和中心对称的内容，利用图形旋转的特征和中心对称的性质来得出平行四边形的性质.
我在设计本课内容的教学时，始终贯穿以中心对称为主线，展开对平行四边形的性质的探索与研究.首先让学生观察生活中的图片，体会到平行四边形在生活中的广泛应用，再由学生动手操作作中心对称三角形得到一个平行四边形，让学生在实际操作过程中加深对中心对称图形的理解，使学生理解平行四边形是由三角形绕其一边的中点旋转180o而成的中心对称图形.紧接着让学生探索讨论画出的四边形两组对边的位置关系，进而得出平行四边形的概念，在教学中引导学生理解图形的概念具有两方面的含义，它既是图形的一条性质，又是判别图形的条件.然后，通过多媒体课件的演示，围绕“图形绕点O旋转180o后，点A与点C、点B与点D分别互换了位置，旋转后的图形与原来的图形重合”这一特征，引导学生探索平行四边形的性质，得出性质后及时巩固符号语言的书写，在练习中规范学生的说理过程.
学生的数学学习的过程不能只是接受现成的数学知识，而是以学生已有的知识和经验为基础的主动建构的过程.本节课注重学生的学习过程，让学生动手操作，画一画，在合作交流中学习，提高学生的学习能力.新课程的核心理念是：“一切为了每一位学生的发展.”在课堂上努力营造一个良好的氛围，让学生去经历、体验、感悟，培养学生的数学能力，给学生提供参与的机会，让学生体验到学习数学的乐趣，从而让学生在课堂上动起来.
在这次教学过程中也发现不少不足之处：(1)性质的探索花的时间较短，因为本节课内容比较多，所以在上课的过程中有点赶，导致后面有多余的时间了，更多的还是应该把时间留给学生，发挥学生的主体地位.(2)虽然运用多媒体技术对于学生不易理解的知识来说效果要好的多，但是学生真正能留下来多少还有待商议.(3)对于练习题中一些没有图形的题目，还是应当让学生自己画画图形，可能对于后进生有更多的帮助，所以在以后的教学中还是得多多关注学生的个体差异.(4)我引导学生思维的语言不够精炼，时间把握的不够好，课堂不够紧凑，这些在今后的教学中要多加注意和改进的.