苏科版 八年级下 9.1反比例函数

课件13张PPT。 新课导入
1、当路程 s 一定时，时间 t 与速度 v 的关系
2、当矩形面积 S一定时，长 a 与宽 b 的关系
3、当三角形面积 S 一定时，三角形的底边 y 与高 x
的关系
tv=sab=sxy=2s你还记得什么是反比例关系吗？如果两个变量x和y满足xy=k（k为常数，
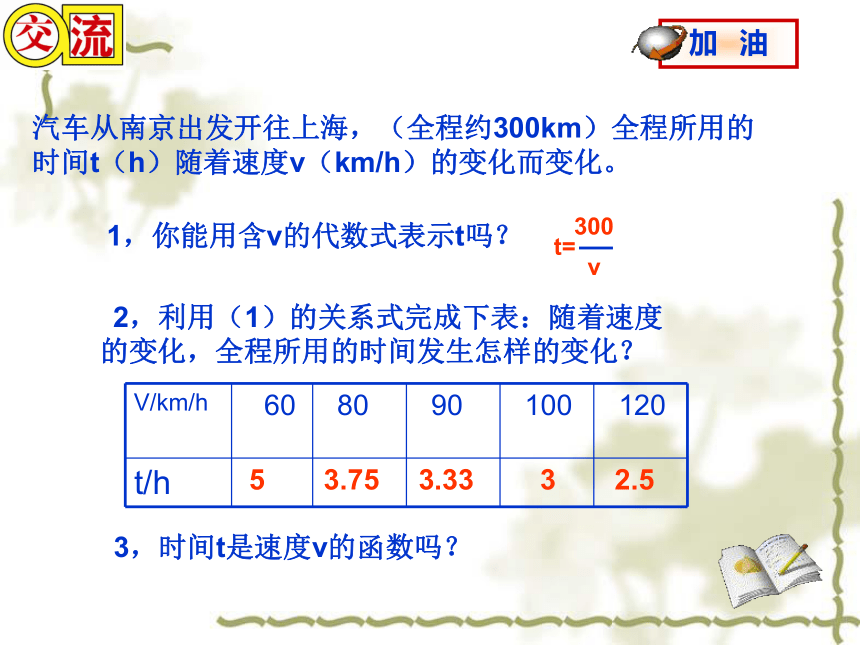
k≠0），那么x和y就是反比例关系。汽车从南京出发开往上海，（全程约300km）全程所用的时间t（h）随着速度v（km/h）的变化而变化。1，你能用含v的代数式表示t吗？ 2，利用（1）的关系式完成下表：随着速度的变化，全程所用的时间发生怎样的变化？3，时间t是速度v的函数吗？t=300v53.753.3332.5用函数关系式表示下列问题中两个变量之间的关系:1 . 一个面积是6400m 的长方形的长a(m)随宽b(m)的变化而变化
则a关于b的关系式为＿＿＿＿＿.22、京沪线铁路全程为１463 km，某列车平均速度为　v（km／
h），全程运行时间为　t（h），则v关于t的关系式为＿＿＿＿＿ 3. 已知三角形的面积是8,它的底边长y与底边上的高x之间的关系
式为＿＿＿＿＿4 . 实数m与n的积是—200,m关于n的关系式为＿＿＿＿＿
由上面的问题中我们得到这样的四个函数1 这些函数关系式有什么共同特征？
2 你能仿照y=kx的形式表示一下上面函数的一般形式吗?
反比例函数反比例函数的定义:反比例函数的自变量的取值范围是不为０的全体实数比例系数一般的,形如 (k为常数,k ≠0) 的函数称
为反比例函数.其中x是自变量，y是x的函数。有时反比例函数也写成y=kx-1或k=xy的形式.试一试例1:下列函数中哪些是反比例函数,并指出比例系数k的值？ 注：形如
的关系式都是反比例函数关系式y=kx-1xy=ky= kxK=4K=-12K=4练习1下列关系式中y是x的反比例函数的是: 1, 2， 4， 3， 5，6，√√√例2:若函数 是反比例函数,求出m的值并写出解析式.分析: 因为函数 是反比例函数,所以x的指数是－１,
即 ,
另外还要保证系数不为0,即m-2≠0.解:由
得m=±2,
又∵m-2≠0, 即 m≠2
∴ m=-2
∴解析式为
或
例3:若y与x成反比例，且x＝－3时，y＝7，则y与x
的函数关系式为______________　1、某住宅小区要种植一个面积为1000 m 的矩形草坪，草坪长
为 y m，宽为 x m,则 y关于 x 的关系式为＿＿＿＿＿＿；
挑战自我23、已知y+2与x-1成反比例，且当x=2时，y=-5，求y与x间的函数关系式，并求出当x=5时y的值。 2，当a= 时，函数是反比例函数？
1提示:设拓展创新1,已知y=y1+y2,y1与x成正比例,y2与x成反比例,并且当
x=2时,y=-4,当x=-1时,y=5,求y与x的函数关系式.