余角补角对顶角（1）

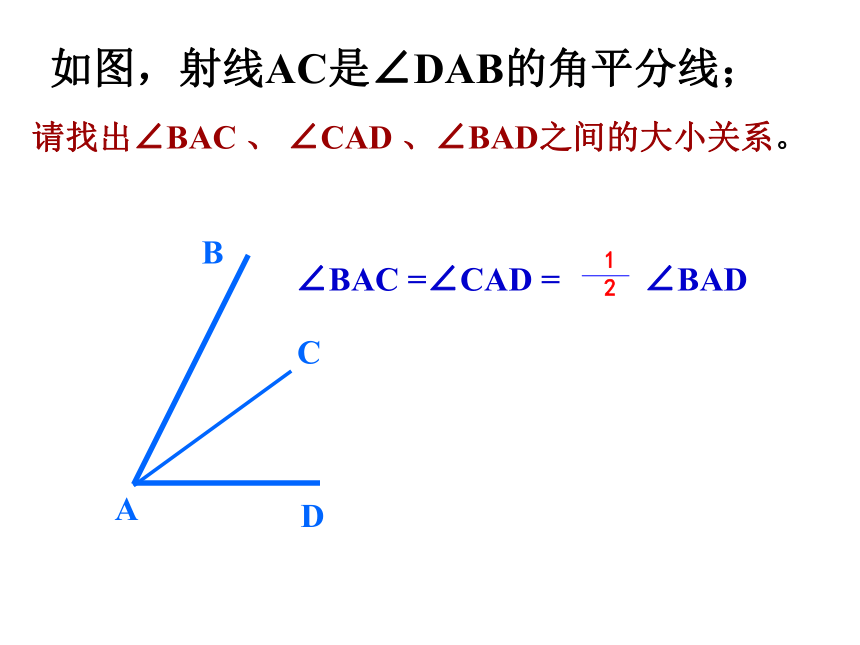
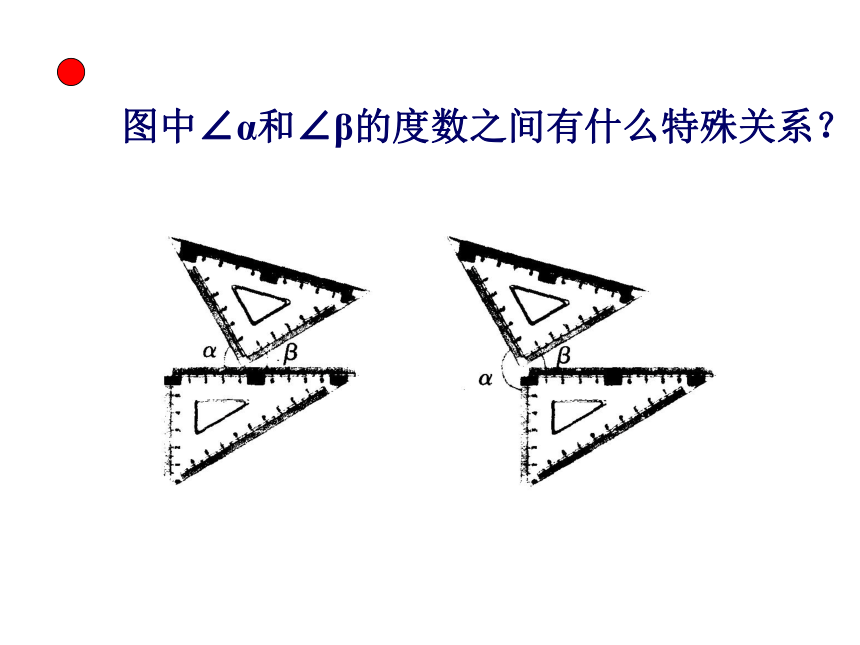
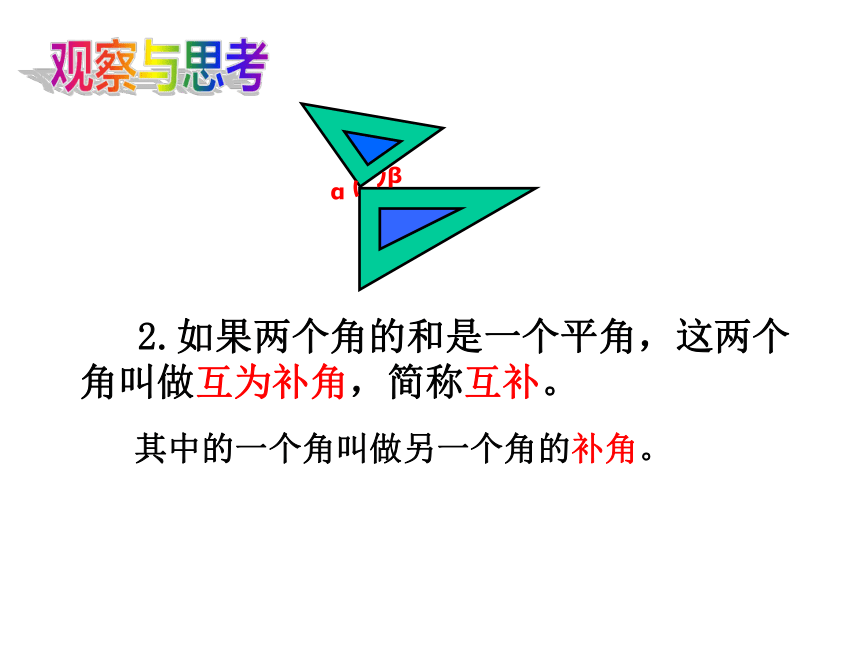
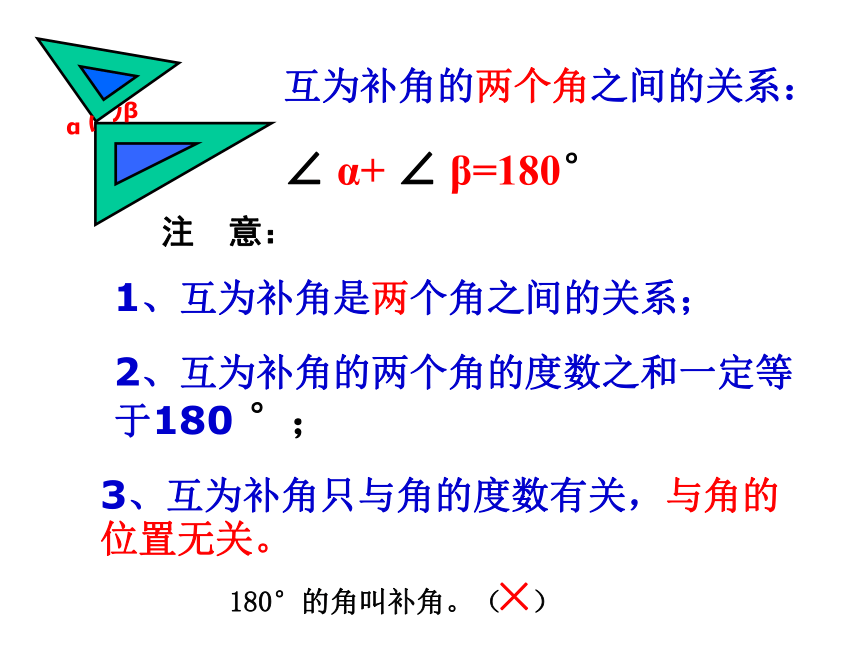
课件27张PPT。6.3 余角 补角 对顶角 宿迁青华外国语学校 孙远亮∠2∠BCE∠BAD∠BAC将图中的角用不同方法表示出来并填写下表 ∠5请找出∠BAC 、 ∠CAD 、∠BAD之间的大小关系。如图，射线AC是∠DAB的角平分线；∠BAC =∠CAD = ∠BAD 图中∠α和∠β的度数之间有什么特殊关系？观察与思考 1.如果两个角的和是一个直角，这两个角叫做互为余角，简称互余。其中的一个角叫做另一个角的余角。互为余角的两个角之间的关系：注 意：∠ α+ ∠ β=90°1、互为余角是两个角之间的关系，不能说三个角互为余角。2、互为余角的两个角的度数的和一定等于90°；3、互为余角只与角的度数有关，与角的位置无关。90°的角叫余角（ ）× 2.如果两个角的和是一个平角，这两个角叫做互为补角，简称互补。其中的一个角叫做另一个角的补角。观察与思考互为补角的两个角之间的关系：注 意：∠ α+ ∠ β=180°1、互为补角是两个角之间的关系；2、互为补角的两个角的度数之和一定等于180 °；3、互为补角只与角的度数有关，与角的位置无关。×180°的角叫补角。（ ）说一说：1、∠ α的余角表示为：
∠ 1的补角表示为：90 °- ∠α180 °- ∠ 12、互为余角的两个角一定都是（ ）角
互为补角的两个角可能是：
_____________;
_____________.锐一个锐角、一个钝角两个都是直角1.填 表0000想一想:同一个角的补角与它的余角之间有怎样的数量关系?知识应用2.已知3组角(1)对A组中的每一个角，在B组中找出它的补角，并用线连接；(2)B组中有哪些角的余角在C组中？分别找出这些角，并用线连接。A组B组C组知识应用同角（或等角）的余角相等；同角（或等角）的补角相等；知识提升知识应用2例1．已知∠A=34o30′，求∠A的余角、补角。解： 因为∠A=34o30′ 所以∠A的余角=90o-∠A =90o-34o30' =55o30' ∠A的补角=180o-∠A =180o-34o30' =145o30‘变式：(1)已知∠A的补角是75o,求∠A (2)已知∠A的余角是37o,求∠A及∠A的补角。练习一：判断：
1．如果∠1=30°，∠2=25°，∠3=35°，那么∠1、∠2、∠3这三个角称为互为余角。（ ）错 （析：互为余角只是对两个角的数量关系而言的）2．两块直角三角板中∠A=90°，∠D=90°，它们互为补角。（ ） 对 （析：互为补角仅仅表明两个角的数量关系，而与角的位置无关。 ）例2．已知一个角的补角是这个角的余角的4倍，求这个角的度数。解：设这个角为x°，则它的余角为(90-x) °，它的补角为(180-x) °，得 180-x=4(90-x) 180-x=360-4x -x+4x=360-18 3x=180 X=60答：这个角是60o。练习二：1．已知∠A的余角是它的2倍，求∠A的度数。
2．已知∠B是它补角的3倍，求∠B的度数。解：设∠A为x°，则它的余角为(2x)°，得
X+2x=90,x=30°
答：∠A是30°。解:设∠B为x°则它的补角为(180-x)°得
X=3(180-x), x=135
答：∠B是135°。例3．如图，∠1和∠2互余，∠3和∠4互余，若∠1=∠3，那么∠2与∠4相等吗？为什么？


证明：∵∠1与∠2互余 ∴∠1+∠2=90o，即∠2=90o-∠1 ∵∠3与∠4互余 ∴∠3+∠4=90o，即∠4=90o-∠3 又∵∠1=∠3 ∴∠2=∠4（等量减等量差相等）例3变式：如果把互余改为互补仍相等吗?
为什么？1243练习三 ：1．如图3-1，若∠1与∠2互余，∠2与∠3互余，则∠ （ ）， =∠（ ），根据是 ； 1 3 2.如图3-2，若∠ 、∠ 互补，∠ 与∠ 互补，则∠ =∠ ，根据是 ；同角的余角相等同角的余角相等练习三 ：3．如图3-3，O是直线AB上的一点，OC平分∠AOB，∠DOE=90o，则
（1）∠2=∠（ ），∠1=∠（ ）
（2）图中，互为余角的角共有哪几对？
（ ）
（3）图中，∠DOB的补角是（ ）。 4 3 ∠1与∠2，∠1与∠4，∠2与∠3，∠4与∠3 ∠1，∠3A1432BCDE3.判断⑴90°的角叫余角，180°的角叫补角。（ ）
⑵如果∠1+ ∠ 2 +∠3=180 ° ，
那么∠1、 ∠ 2与∠3互补。 （ ）××2.如图，如果∠1与∠ 2互补， ∠ 3与∠4互补， ∠1 =∠ 3,那么∠2与∠4相等吗？为什么？1.如图，如果∠1与∠ 2互余， ∠ 3 与∠4互余， ∠1 =∠ 3,那么∠2与∠4相等吗？为什么？想一想?三、当堂反馈 一、判断：
（1）如果两个角相等，则它们的补角相等。 （ ）
（2）如果∠1 =40 °，∠2=60 °，∠3 =80 °，
那么∠1、 ∠2、 ∠3互为补角。 （ ）
二、填空：
（1）一个角是36 ° ，则它的余角是_______，它的补角是_____。
（2） ∵ ∠1和∠2互余，∴ ∠2=_____- ∠1；
∵ ∠1和∠2互补，∴ ∠1=_____- ∠2 。
三、如图， ∠AOB= ∠COD=90 °，
则∠BOC与∠AOD有怎样的大小关系？为什么？√×54°144°90°180°解： ∠ BOC = ∠AOD.
因为∠AOC与∠ BOC互余，∠AOC与∠AOD互余，
而同角的余角相等，
所以∠ BOC = ∠AOD.课后思考:如图, ∠1与∠2互补,则∠1与 (∠2-∠1)和的关系为( )。
A．互补 B.互余 C.相等 D.小于的度数。拓　展　练　习１.如果∠１＝∠２，∠２＝∠３，那么∠１　　　∠３；　如果∠１＞∠２，∠２＞∠３，那么∠１　　　∠３。２.如图，直线CD经过点O，且OC平分∠AOB。∠AOD与∠BOD有怎样的大小关系？为什么？说一说你学到了什么