人教版五年级上册数学5.5 等式的性质-课件(20张ppt)
文档属性
| 名称 | 人教版五年级上册数学5.5 等式的性质-课件(20张ppt) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-27 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
第5单元 简易方程
5 等式的性质
学习目标
2.能用等式的性质解决简单问题。
1.理解并能用语言表述等式的性质。
3.体验探索等式的基本性质和数学结论的确定性。
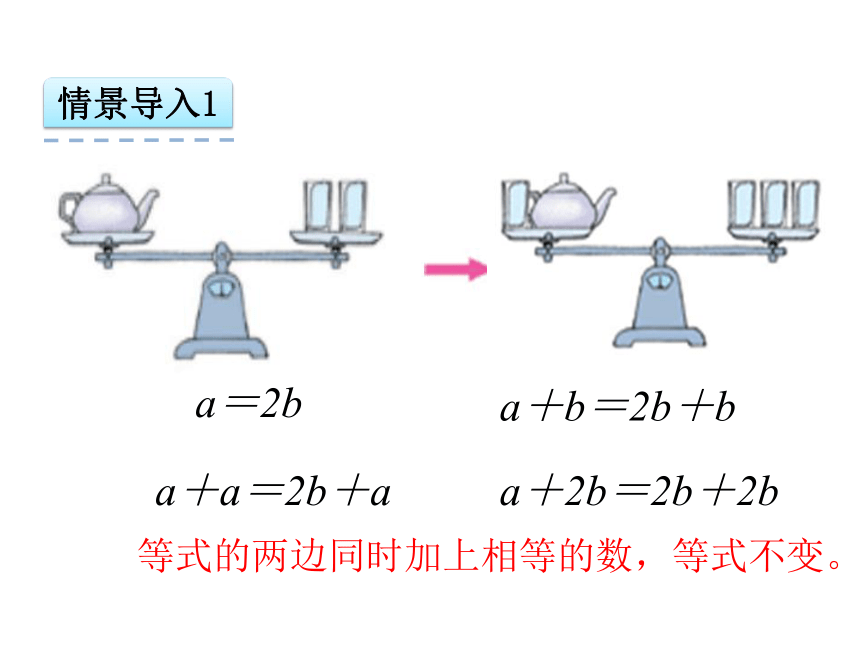
等式的两边同时加上相等的数,等式不变。
a=2b
a+b=2b+b
a+2b=2b+2b
a+a=2b+a
情景导入1
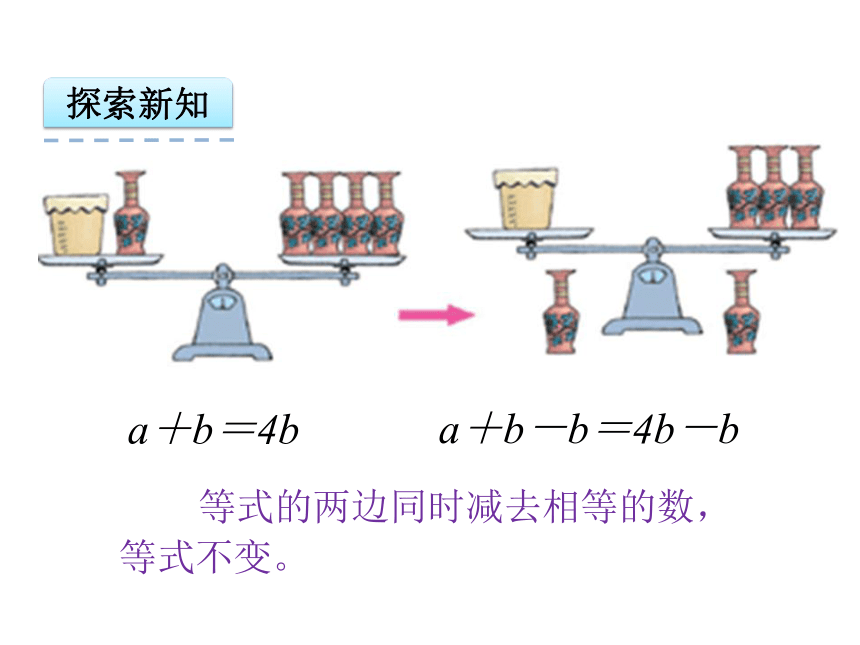
等式的两边同时减去相等的数,等式不变。
a+b=4b
a+b-b=4b-b
探索新知
等式的两边同时乘或除以相等的数,等式变吗?
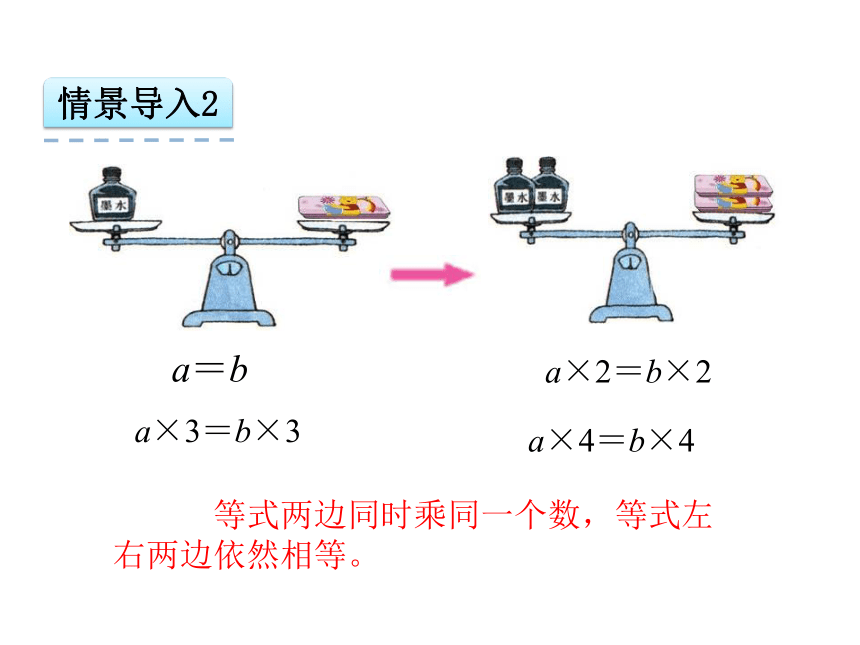
等式两边同时乘同一个数,等式左右两边依然相等。
a×2=b×2
a=b
a×3=b×3
a×4=b×4
情景导入2
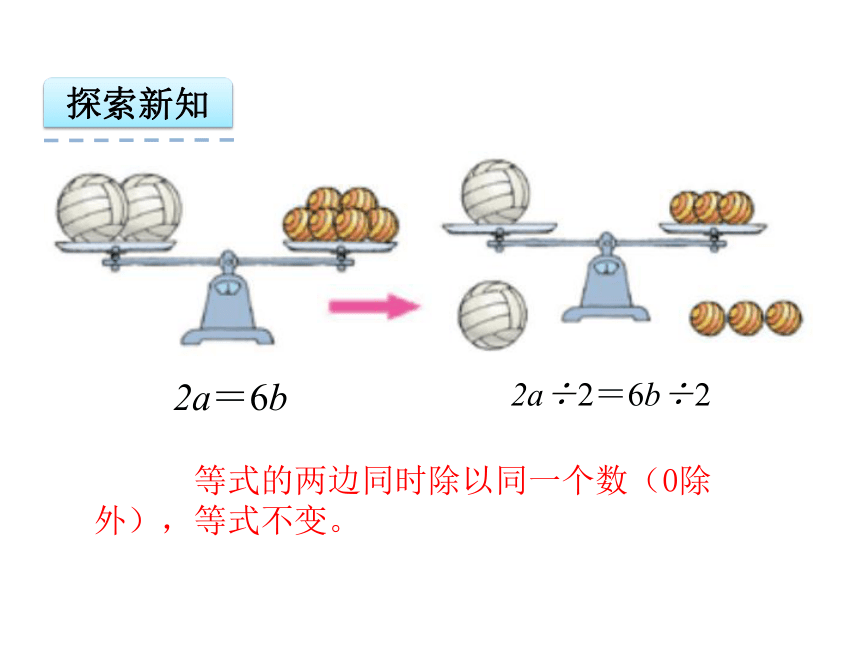
等式的两边同时除以同一个数(0除外),等式不变。
探索新知
2a÷2=6b÷2
2a=6b
等式的性质1 等式两边同时加上(或减去)同一个数,等式仍然成立。
等式的性质2 等式两边同时乘同一个数(或除以同一个不为0的数),等式仍然成立。
探索新知
典题精讲
判断:
若2x+6=8,则2x=14。( )
典题精讲
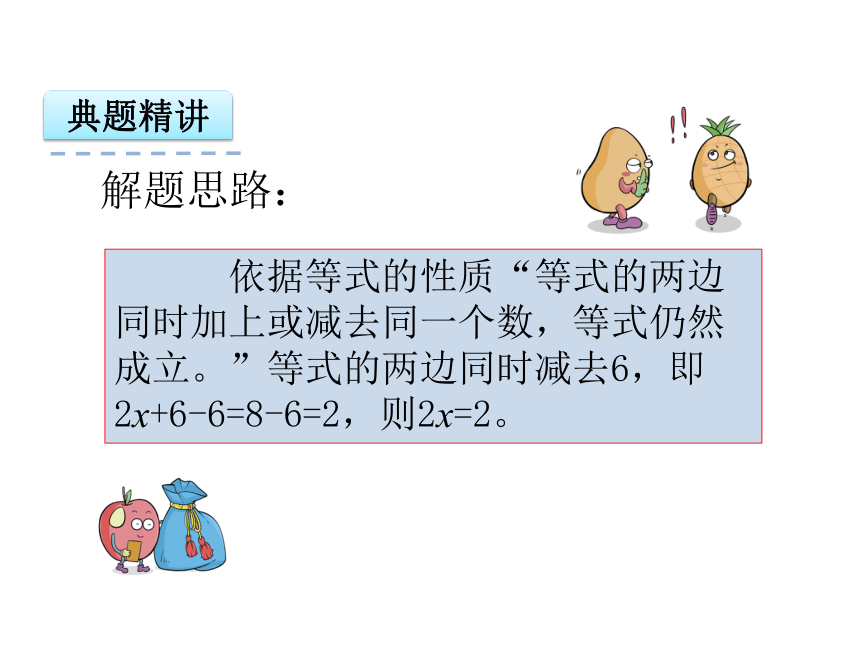
解题思路:
依据等式的性质“等式的两边同时加上或减去同一个数,等式仍然成立。”等式的两边同时减去6,即2x+6-6=8-6=2,则2x=2。
若2x+6=8,则2x=14。( )
典题精讲
×
正确解答:
判断:若6x=72,则6x÷6=72。 ( )
易错提醒
错误解答
√
错解分析:
易错提醒
错误解答错在没有掌握等式的性质。等式的性质“等式的两边同时乘或除以同一个数(0除外),等式仍然成立。”等式的两边同时除以6,即6x÷6=72÷6=12,则x=12。
易错提醒
正确解答
错误解答
判断:若6x=72,则6x÷6=72。 ( )
√
判断:若6x=72,则6x÷6=72。 ( )
×
若X=Y ,则下列等式是否成立,
若成立,请指明依据等式的哪条性质。
(1)X+ 5=Y+ 5
(2)X - a = Y - a
(3)(5-a)X=(5-a)Y
等式的性质1
等式的性质1
等式的性质2
学以致用
如果a=b,根据等式的性质填空。
a+3=b+( )
a-( )=b-c
a×d=b×( )
a÷( )=b÷10
3
c
d
10
学以致用
要保持天平平衡,右边应该添加什么物品?
学以致用
判断:
学以致用
1.如果a=b,那么a+5=b+5。( )
2.如果6+a=b-6,那么a=b。( )
3.如果a=b,那么a×5=b×5。( )
4.如果a=b,那么a÷3=3÷b。( )
×
√
√
×
观察下面的天平,列出式子。
学以致用
x+20=50+20
课堂小结
你学会了哪些知识?
同时加或减必须是同一个数;同时乘或除以也是同一个数,但是除以的数不能是0。
1. 等式两边加上或减去同一个数,左右两边仍然相等。
2.等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
谢谢
第5单元 简易方程
5 等式的性质
学习目标
2.能用等式的性质解决简单问题。
1.理解并能用语言表述等式的性质。
3.体验探索等式的基本性质和数学结论的确定性。
等式的两边同时加上相等的数,等式不变。
a=2b
a+b=2b+b
a+2b=2b+2b
a+a=2b+a
情景导入1
等式的两边同时减去相等的数,等式不变。
a+b=4b
a+b-b=4b-b
探索新知
等式的两边同时乘或除以相等的数,等式变吗?
等式两边同时乘同一个数,等式左右两边依然相等。
a×2=b×2
a=b
a×3=b×3
a×4=b×4
情景导入2
等式的两边同时除以同一个数(0除外),等式不变。
探索新知
2a÷2=6b÷2
2a=6b
等式的性质1 等式两边同时加上(或减去)同一个数,等式仍然成立。
等式的性质2 等式两边同时乘同一个数(或除以同一个不为0的数),等式仍然成立。
探索新知
典题精讲
判断:
若2x+6=8,则2x=14。( )
典题精讲
解题思路:
依据等式的性质“等式的两边同时加上或减去同一个数,等式仍然成立。”等式的两边同时减去6,即2x+6-6=8-6=2,则2x=2。
若2x+6=8,则2x=14。( )
典题精讲
×
正确解答:
判断:若6x=72,则6x÷6=72。 ( )
易错提醒
错误解答
√
错解分析:
易错提醒
错误解答错在没有掌握等式的性质。等式的性质“等式的两边同时乘或除以同一个数(0除外),等式仍然成立。”等式的两边同时除以6,即6x÷6=72÷6=12,则x=12。
易错提醒
正确解答
错误解答
判断:若6x=72,则6x÷6=72。 ( )
√
判断:若6x=72,则6x÷6=72。 ( )
×
若X=Y ,则下列等式是否成立,
若成立,请指明依据等式的哪条性质。
(1)X+ 5=Y+ 5
(2)X - a = Y - a
(3)(5-a)X=(5-a)Y
等式的性质1
等式的性质1
等式的性质2
学以致用
如果a=b,根据等式的性质填空。
a+3=b+( )
a-( )=b-c
a×d=b×( )
a÷( )=b÷10
3
c
d
10
学以致用
要保持天平平衡,右边应该添加什么物品?
学以致用
判断:
学以致用
1.如果a=b,那么a+5=b+5。( )
2.如果6+a=b-6,那么a=b。( )
3.如果a=b,那么a×5=b×5。( )
4.如果a=b,那么a÷3=3÷b。( )
×
√
√
×
观察下面的天平,列出式子。
学以致用
x+20=50+20
课堂小结
你学会了哪些知识?
同时加或减必须是同一个数;同时乘或除以也是同一个数,但是除以的数不能是0。
1. 等式两边加上或减去同一个数,左右两边仍然相等。
2.等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
谢谢
