直线和圆的位置关系

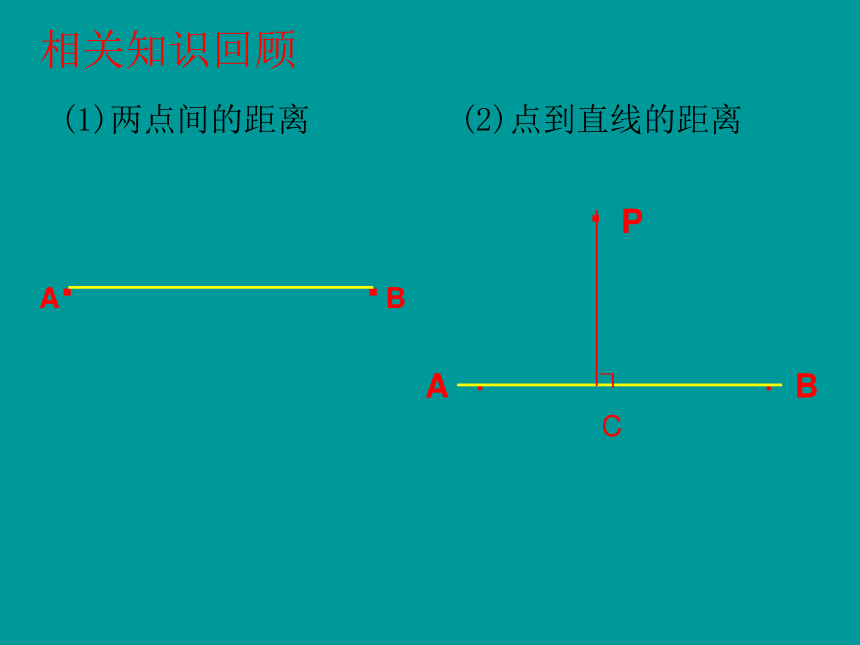
课件21张PPT。直线和圆的位置关系 咱 俩 啥 关 系 ？相关知识回顾(1)两点间的距离(2)点到直线的距离A· ·BC点和圆的位置关系有哪几种？
复习：？猜想：如果把点换成直线呢？
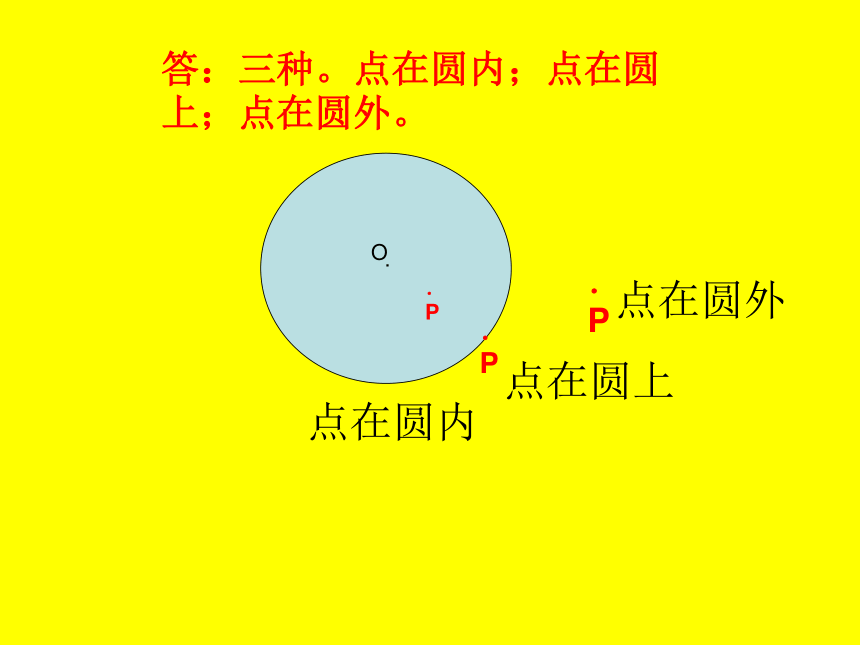
【请同学们先画一个圆，再用直尺的一边当直线并任意移动，观察直线和圆的位置关系有几种？】点在圆内．P．P点在圆上
．P点在圆外答：三种。点在圆内；点在圆上；点在圆外。
点和圆的
位置关系
有三种
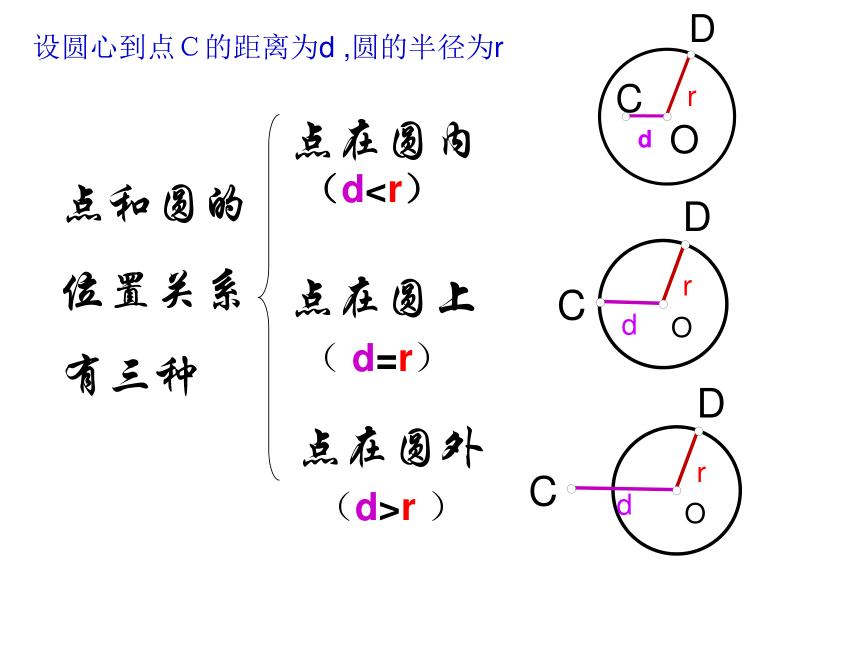
点在圆外点在圆上点在圆内drOCDdrOCDdrOCD设圆心到点Ｃ的距离为d ,圆的半径为r
（d（ d=r）（d>r ）
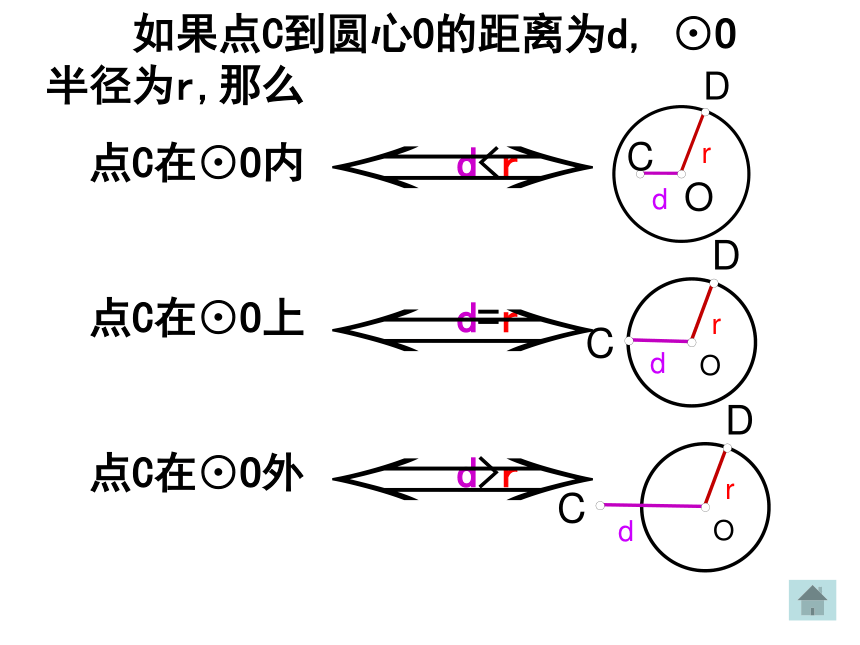
如果点C到圆心O的距离为d, ⊙O半径为r,那么
点C在⊙O内 d
点C在⊙O上 d=r

点C在⊙O外 d>r
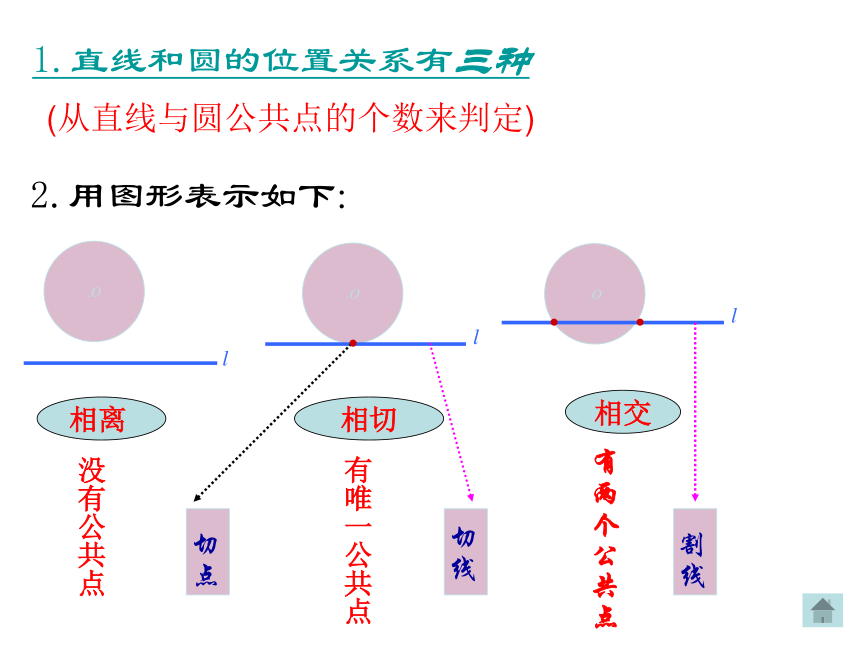
drOCDdrOCDdrOCD·l(一）直线和圆的位置关系1.直线和圆的位置关系有三种
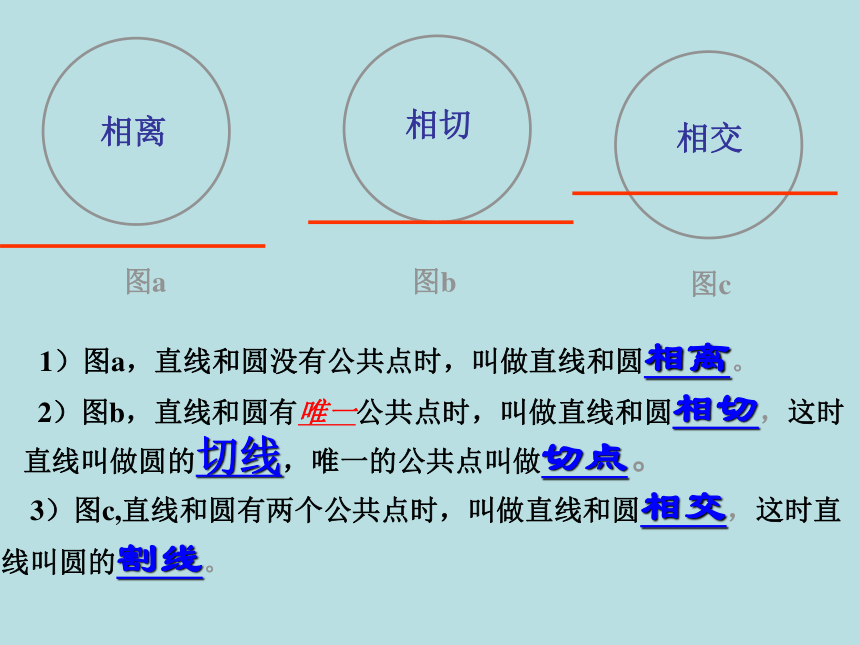
2.用图形表示如下:.O.O.Olll相离 相切相交切线切点割线...有两个公共点有唯一公共点没有公共点(从直线与圆公共点的个数来判定)图a图b图c 2）图b，直线和圆有唯一公共点时，叫做直线和圆相切，这时直线叫做圆的切线，唯一的公共点叫做切点。1）图a，直线和圆没有公共点时，叫做直线和圆相离。 3）图c,直线和圆有两个公共点时，叫做直线和圆相交，这时直线叫圆的割线。
相交相离相切直线和圆除了上述三种位置关系外，有第四种关系吗?即一条直线和圆的公共点能否
多于两个?为什么??（二） 直线和圆的位置关系的性质和判定ordo?rdo?lll (1) 直线l和?O相离d>r<符号“?”读作“等价于”。它表示从左端可以
推出右端，并且从右端也可以推出左端。(2) 直线l和?O相切d=rrd(3) 直线l和?O相交d1、直线和圆有公共点,这条直线叫做圆的割线.( )
2、直线和圆有公共点,这条直线叫做圆的切线.( )
3、直线和圆相切,直线和圆有唯一的公共点. ( )
4、圆心到直线的距离等于半径,这条直线叫圆的切线. ( )
5、直线过圆上一点，这时直线是圆的切线。( )
6、直线是圆的切线，必须在直线上有唯一的点到圆心距离等于半径。( )
7、直线过圆外两点，这时直线与圆相离。( )
8、已知⊙O的半径为4cm，直线l上的点A满足OA=4cm，所以直线l和⊙O相切。( )填空：
已知⊙O的直径为13cm，若直线l与圆心O的距离d=4.5cm时，直线与圆的位置关系是___________，有________个交点，此时直线叫圆的_________；
当d=6.5cm时，直线与圆的位置关系是________，有_________个交点，此时直线叫圆的__________.
当d=8cm时，直线与圆的位置关系是________，有_____个交点。 相切210相交割线切线相离练习： 已知圆心和直线的距离为4cm，如果圆和直线的关系分别为以下情况，那么圆的直径应分别取怎样的值？为什么?（1）相交；（2）相切；（3）相离。答：（1）直径大于8cm时直线和圆相交；
（2）直径等于8cm时直线和圆相切 ;
（3）直径小于8cm时直线和圆相离.例题讲解例 在Rt?ABC中, ?C=90°, AC=3cm, BC=4cm, 以C为圆
心, r 为半径的圆与AB有怎样的位置关系? 为什么?
(1) r =2cm ; (2) r =2.4cm ; (3) r =3cm.ABDC(1)DBC(2)ACBD(3)解：过C作CD⊥AB，垂足为D（如上图）.在Rt?ABC中,根据勾股定理
得:AB=5cm. 再根据三角形的面积公式有 CD·AB=AC·BC,
∴CD=2.4cm 即圆心C到AB的距离d=2.4cm.(1) 当 r = 2cm时, 有 d > r, 因此?C和AB相离.(2) 当 r = 2.4cm时, 有 d = r, 因此?C和AB相切.(3) 当 r = 3cm时, 有 d < r, 因此?C和AB相交. 分析：因为题目给出了⊙O的半径，所以解题关键是求圆心C到直线AB的距离，也就是要求出Rt△ABC斜边AB上的高.因此,可过C点向AB作垂线段CD，然后根据CD的长度与r进行比较，来确定⊙C与AB的关系. 如图，已知∠AOB=300，M为OB上一点，且OM=5cm，以M为圆心，r为半径的圆 和直线OA有怎样的位置关系？为什么？
（1）r =2cm；（2）r =4cm；（3）r =2.5cm。解：作MC⊥OA于C，
在Rt△OCM中，∠AOB=300即圆心M到OA的距离d=2.5cm（1）当r =2cm时，有d ＞ r ，因此⊙ M与OA相离；
（2）当r =4cm时，有d ＜ r ，因此⊙ M与OA相交；
（3）当r =2.5cm时，有d = r ，因此⊙ M与OA相切；300
ABCOM5（１）圆心O到直线l的距离为d,⊙O的半径为R，若d、R是方程x2－4x＋m＝0的两根，且直线l与⊙O相切，则m的值是________．（2006.山东）（２）设⊙O的半径为r,点O到直线l的距离为d,若⊙O与l最多只有一个公共点，则d与r的关系为_________.（2005.河北）d≥ r中　考　考　场4 在△ABC中，AD为BC边上的高，AD＝1/2BC，E、F分别是AB、AC的中点，则以EF为直径的圆与BC的位置关系是_____. (2005.河南)中 考 考 场相切M思考题:如图，公路MN和公路PQ在点P处交汇，且∠APN＝30o,点A处有一所学校，AP＝160m,假设拖拉机行驶,周围100 m内会受噪音影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受影响.请说明理由.如果受影响,已知拖拉机的速度为18m/s,那么学校受影响的时间为多少秒?(2006.青岛)AM●300PNBDC解:学校受噪音的影响.理由如下:
过点A作AB⊥MN于点B.在Rt△ABP中， ∠APN＝30o, AP＝160m，所以AB= 80m. ∵ AB<100 ∴学校受噪音的影响.在MN上取AC=AD=100m.
在Rt△ABC中, ∵ AB= 80m, AC=100m, ∴BC=60m.同理,BD=60m. ∴120÷18=20/3秒.
∴学校受影响的时间为20/3秒.请同学们填写下表：相离 0——d>r直线1个 切点d=r切线2个交点d1、课本第58页第2、3题
2、几何质量检测32页1——6题。
研究体验性练习：
1、完成练习题（二）
2、课余时间，留心观察周围事物，找出直线和圆相交，相切，相离的实例，说给大家听。
预习性作业：
6.8 切线的画法、判定和性质。