12.2 三角形全等的判定(HL)教学课件
文档属性
| 名称 | 12.2 三角形全等的判定(HL)教学课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 259.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-28 00:00:00 | ||
图片预览


文档简介
课件17张PPT。
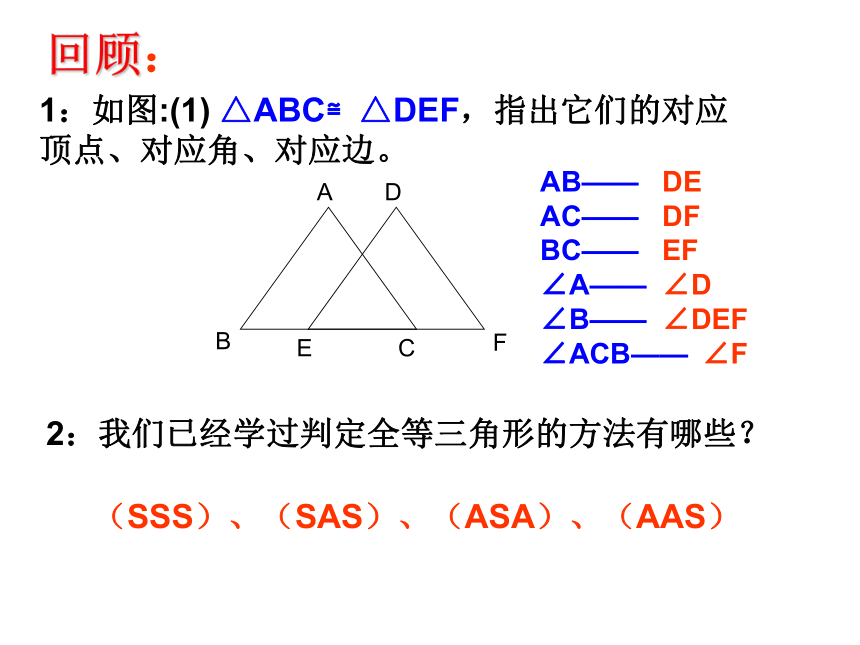
直角三角形全等的条件(HL)回顾:2:我们已经学过判定全等三角形的方法有哪些?AB——
AC——
BC——
∠A——
∠B——
∠ACB——(SSS)、(SAS)、(ASA)、(AAS)DE
DF
EF
∠D
∠DEF
∠F回
顾
与
练
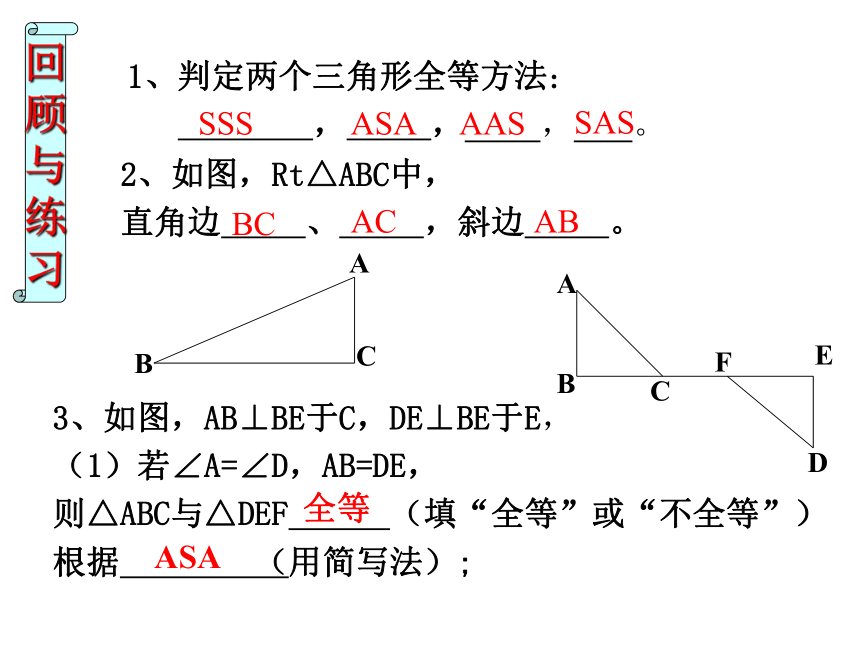
习1、判定两个三角形全等方法:
, , , 。SSSASAAASSAS2、如图,Rt△ABC中,
直角边 、 ,斜边 。BCACAB3、如图,AB⊥BE于C,DE⊥BE于E,
(1)若∠A=∠D,AB=DE,
则△ABC与△DEF (填“全等”或“不全等”)
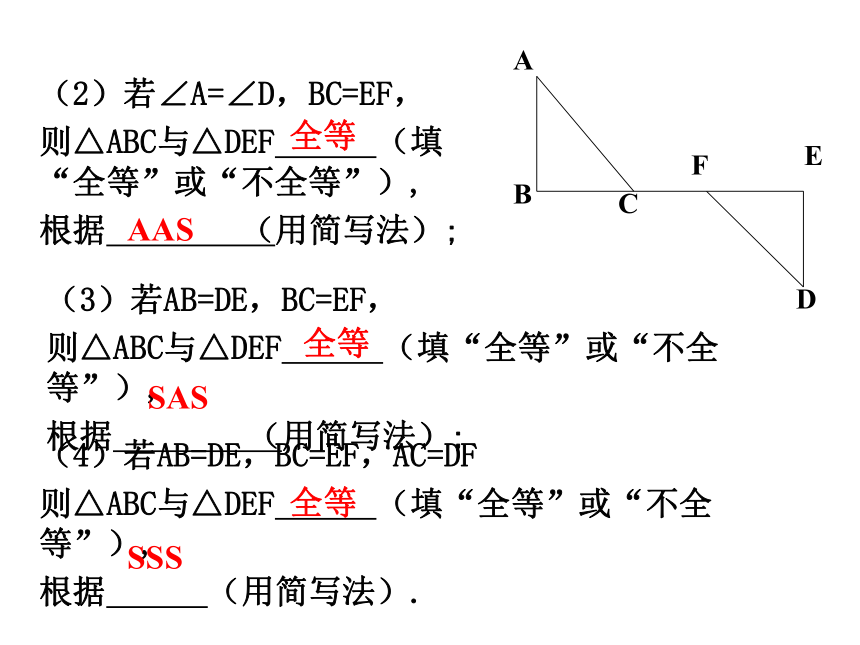
根据 (用简写法);全等ASA(2)若∠A=∠D,BC=EF,
则△ABC与△DEF (填“全等”或“不全等”),
根据 (用简写法);AAS全等(3)若AB=DE,BC=EF,
则△ABC与△DEF (填“全等”或“不全等”),
根据 (用简写法);全等SAS(4)若AB=DE,BC=EF,AC=DF
则△ABC与△DEF (填“全等”或“不全等”),
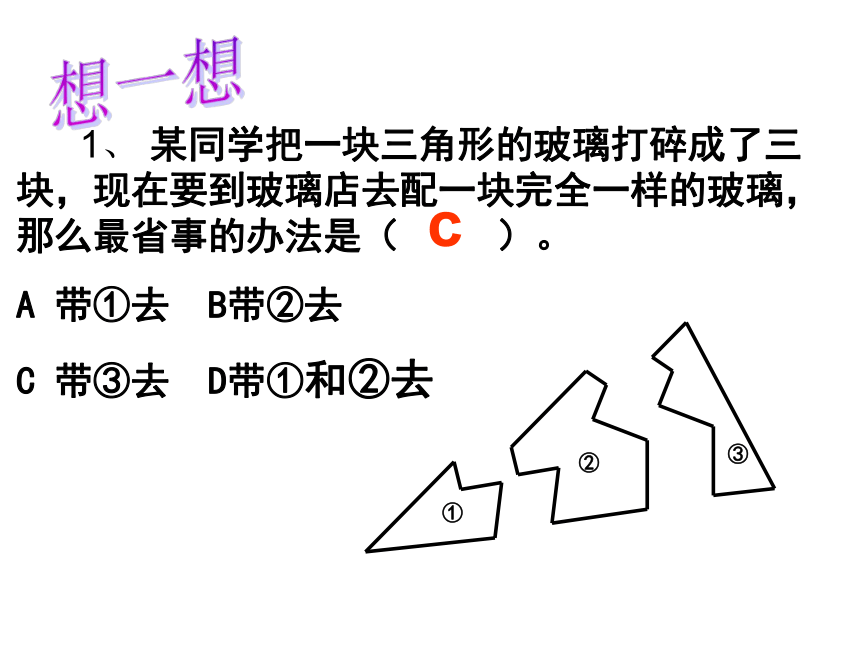
根据 (用简写法).全等SSS 1、 某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )。
A 带①去 B带②去
C 带③去 D带①和②去
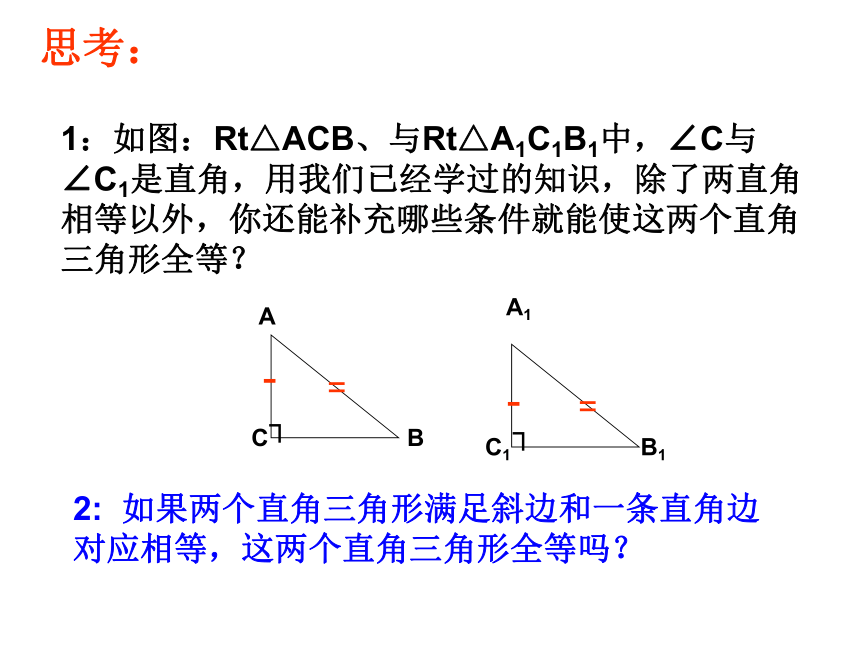
想一想c2: 如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?┐┐--==画一画:
任意画一个Rt△ACB ,使∠C﹦90°,
再画一个Rt△A′C′B′使∠C=∠C′,
B′C′=BC,A′B′=AB
(1):你能试着画出来吗?与小组交流一下。作法:
1、画∠MC′N=90°
2、在射线C′M上取B′C′=BC
3、以B′为圆心,AB为半径画弧,交射线C′N于点A′
4、连接A′B′,△A′C′B′就是所作三角形。(2):把画好的Rt△A′C′B′剪下,放到Rt△ACB上,它们全等吗?你能发现什么规律? 如图, △ABC中, ∠C是直角斜边直角边直角边直角三角形用Rt△
表示。学习目标:
1、理解直角三角形全等的判定方法-斜边直角边;
2、熟练运用“HL”定理证明执教三角形全等;
3、熟练运用“HL”定理解决有关问题.做一做用尺规作图法,做一个Rt△ABC,使∠C= 90°斜边AB=10cm,一直角边CB=6cm.
剪下这个三角形,和其他同学所作的三角形进行比较,它们能重合吗?
想一想,怎样画呢?按照下面的步骤做一做:⑴ 作∠MCN=90°;⑵ 在射线CM上截取线段CB=6cm;⑶ 以点B为圆心,以10cm为半径画弧,交射线CN于点A;⑷ 连接AB. 用符号语言表达为:
在Rt△ACB和Rt△DFE中,
AB=DF
AC=DF
∴Rt△ACB≌Rt△DFE(HL)注意:使用HL判定时,必须先得出两个直角三角形,然后再证明斜边和一直角边分别对应相等。
任意画出一个Rt△ABC,使∠C=90, 再画一个Rt△A′B′C′,使∠C′=90o,B′C′=BC,A′B′=AB.它们全等吗?即使斜边和一条直角边对应相等AB = DEAC= DFRt △ABC ≌ Rt △ DEF(HL)ABCDEF 斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)? 记一记 ? 练一练≌练一练若根据“HL”判定,还需要加条件:
, ;
或: , 。AD = BDBE=ACBE=ACDE=DC如图:AC⊥BC,BD⊥AD,AC=BD.求证:BC=AD.你还能找到其他的全等三角形吗?
你可以得到哪些线段相等?
直角三角形全等的条件(HL)回顾:2:我们已经学过判定全等三角形的方法有哪些?AB——
AC——
BC——
∠A——
∠B——
∠ACB——(SSS)、(SAS)、(ASA)、(AAS)DE
DF
EF
∠D
∠DEF
∠F回
顾
与
练
习1、判定两个三角形全等方法:
, , , 。SSSASAAASSAS2、如图,Rt△ABC中,
直角边 、 ,斜边 。BCACAB3、如图,AB⊥BE于C,DE⊥BE于E,
(1)若∠A=∠D,AB=DE,
则△ABC与△DEF (填“全等”或“不全等”)
根据 (用简写法);全等ASA(2)若∠A=∠D,BC=EF,
则△ABC与△DEF (填“全等”或“不全等”),
根据 (用简写法);AAS全等(3)若AB=DE,BC=EF,
则△ABC与△DEF (填“全等”或“不全等”),
根据 (用简写法);全等SAS(4)若AB=DE,BC=EF,AC=DF
则△ABC与△DEF (填“全等”或“不全等”),
根据 (用简写法).全等SSS 1、 某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )。
A 带①去 B带②去
C 带③去 D带①和②去
想一想c2: 如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?┐┐--==画一画:
任意画一个Rt△ACB ,使∠C﹦90°,
再画一个Rt△A′C′B′使∠C=∠C′,
B′C′=BC,A′B′=AB
(1):你能试着画出来吗?与小组交流一下。作法:
1、画∠MC′N=90°
2、在射线C′M上取B′C′=BC
3、以B′为圆心,AB为半径画弧,交射线C′N于点A′
4、连接A′B′,△A′C′B′就是所作三角形。(2):把画好的Rt△A′C′B′剪下,放到Rt△ACB上,它们全等吗?你能发现什么规律? 如图, △ABC中, ∠C是直角斜边直角边直角边直角三角形用Rt△
表示。学习目标:
1、理解直角三角形全等的判定方法-斜边直角边;
2、熟练运用“HL”定理证明执教三角形全等;
3、熟练运用“HL”定理解决有关问题.做一做用尺规作图法,做一个Rt△ABC,使∠C= 90°斜边AB=10cm,一直角边CB=6cm.
剪下这个三角形,和其他同学所作的三角形进行比较,它们能重合吗?
想一想,怎样画呢?按照下面的步骤做一做:⑴ 作∠MCN=90°;⑵ 在射线CM上截取线段CB=6cm;⑶ 以点B为圆心,以10cm为半径画弧,交射线CN于点A;⑷ 连接AB. 用符号语言表达为:
在Rt△ACB和Rt△DFE中,
AB=DF
AC=DF
∴Rt△ACB≌Rt△DFE(HL)注意:使用HL判定时,必须先得出两个直角三角形,然后再证明斜边和一直角边分别对应相等。
任意画出一个Rt△ABC,使∠C=90, 再画一个Rt△A′B′C′,使∠C′=90o,B′C′=BC,A′B′=AB.它们全等吗?即使斜边和一条直角边对应相等AB = DEAC= DFRt △ABC ≌ Rt △ DEF(HL)ABCDEF 斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)? 记一记 ? 练一练≌练一练若根据“HL”判定,还需要加条件:
, ;
或: , 。AD = BDBE=ACBE=ACDE=DC如图:AC⊥BC,BD⊥AD,AC=BD.求证:BC=AD.你还能找到其他的全等三角形吗?
你可以得到哪些线段相等?
