七年级数学(北师大版)导学案(无答案):5.3 应用一元一次方程——水箱变高了
文档属性
| 名称 | 七年级数学(北师大版)导学案(无答案):5.3 应用一元一次方程——水箱变高了 |
|
|
| 格式 | zip | ||
| 文件大小 | 17.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-29 00:00:00 | ||
图片预览


文档简介
科目
数学
课题
5.3应用一元一次方程—水箱变高了
主备人
审核人
课型
新授
学案编号
学
习
目
标
知识与能力:通过分析图形问题中的数量关系,建立方程解决问题.
过程与方法:进一步体会运用方程解决问题的关键是抓住等量关系,认识方程模型的重要性。
情感态度和价值观:通过对实际问题的探讨,使学生在动手独立思考、方程意识的过程中,进一步体会数学应用的价值,鼓励学生大胆质疑,激发学生的好奇心和主动学习的欲望.
重点:列出一元一次方程解有关形积变化问题;依题意准确把握形积问题中的相等关系。
难点:一元一次方程解有关形积变化问题;依题意准确把握形积问题中的相等关系。
学法指导及使用说明:启发式教学
知识链接:
一、学习流程:1、用同一块橡皮泥捏出不同形状的几何体。(1)想想它有何变化?(2)你发现有什么相等关系?2.填空:长方形的周长=
面积=
长方体的体积=
正方体的体积=
圆的周长=
面积
=
圆柱的体积=
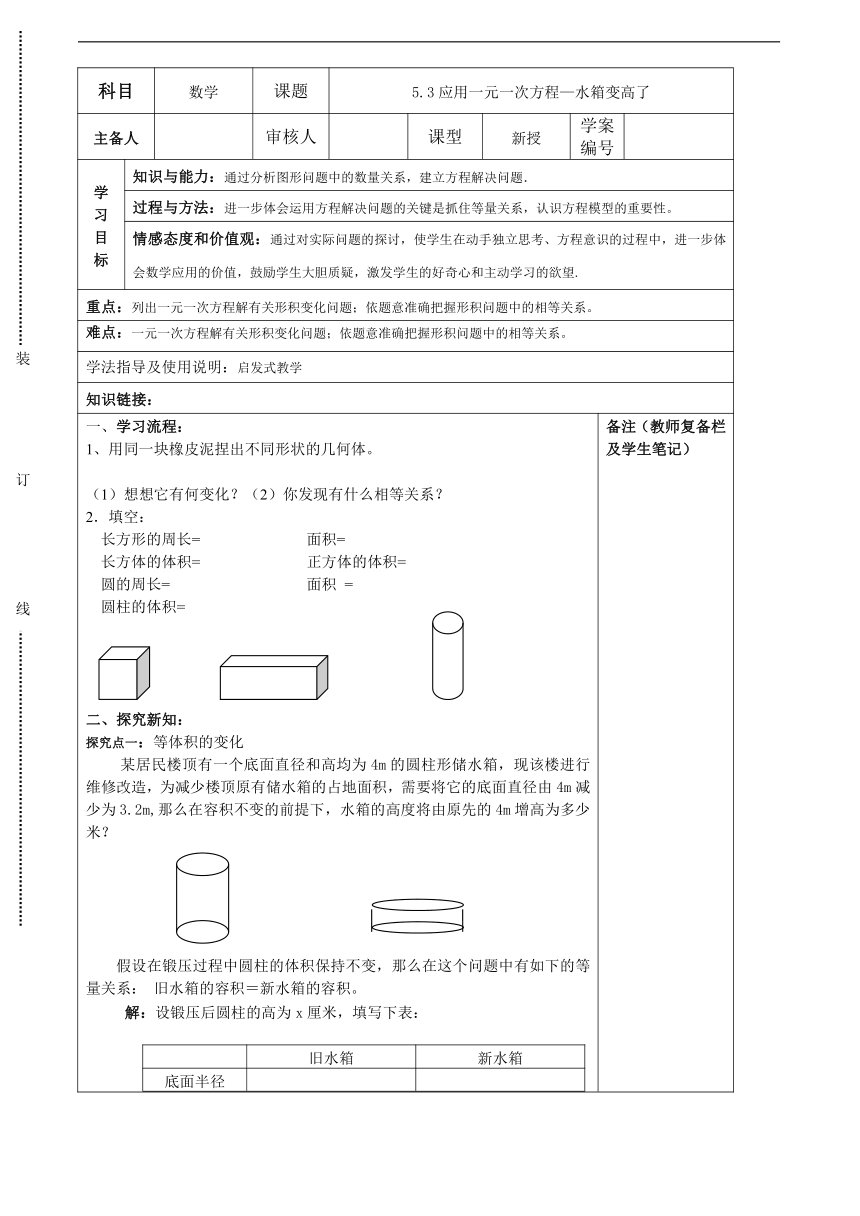
二、探究新知:探究点一:等体积的变化某居民楼顶有一个底面直径和高均为4m的圆柱形储水箱,现该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4m减少为3.2m,那么在容积不变的前提下,水箱的高度将由原先的4m增高为多少米?
假设在锻压过程中圆柱的体积保持不变,那么在这个问题中有如下的等量关系:
旧水箱的容积=新水箱的容积。解:设锻压后圆柱的高为x厘米,填写下表:旧水箱新水箱底面半径高体积
根据等量关系,列出方程:
(接着解方程)
答:水箱的高变成了
米。探究点二:等周长的变化1、用一根长为10米的铁丝围成一个长方形。(1)使得该长方形的长比宽多1.4米,此时长方形的长、宽各为多少米?面积为多少?解:设此时长方形的宽为
米,则它的长为
米。根据题意,得:(列方程并解方程)
它所围成的长方形的长为
此时所围成的长方形面积为:
(2)使得该长方形的长比宽多0.8米,此时长方形的长、宽各为多少米?它所围成的长方形与(1)中所围长方形相比,面积有什么变化?
解:设长方形的宽为
米,则它的长为
米。根据题意,得:(列方程并解方程)
它所围成的长方形的长为:
此时所围成的长方形面积为:
此时与(1)中所围成的长方形的面积相比,情况如何?(3)使得该长方形的长与宽相等,即围成一个正方形,此时正方形的边长是多少米?它所围成的面积与(2)中的长方形面积相比又有什么变化?解:设正方形的边长为
米。根据题意,得:(列方程并解方程)
此时所围成的正方形的面积为
此时与(2)中所围成的长方形的面积相比,情况如何?三、达标测评(1)圆柱的直径是8厘米,高6厘米,大圆柱的直径是10厘米,并且它的体积是小圆柱体体积的2.5倍,那么大圆柱的高是多少?
(2)墙上钉着用一根彩绳围成的梯形形状的饰物,如右图实线所示。小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如右图虚线所示。小颖所钉长方形的长、宽各为多少厘米?(3)将一个长、宽、高分别为15cm,12cm和8cm的长方形钢块锻造成一个底面边长为12cm的正方形的长方体零件钢坯,试问锻造前长方体的钢块表面积大还是锻造后的长方体零件钢坯表面积大?请你计算比较。(4)第一块试验田的面积比第一块试验田的面积的3倍还多100平方米,这两块试验田的面积共2900平方米,两块实验田的面积分别是多少?四、谈谈你的收获?五、你还有那些疑问?
备注(教师复备栏及学生笔记)
装
订
线
数学
课题
5.3应用一元一次方程—水箱变高了
主备人
审核人
课型
新授
学案编号
学
习
目
标
知识与能力:通过分析图形问题中的数量关系,建立方程解决问题.
过程与方法:进一步体会运用方程解决问题的关键是抓住等量关系,认识方程模型的重要性。
情感态度和价值观:通过对实际问题的探讨,使学生在动手独立思考、方程意识的过程中,进一步体会数学应用的价值,鼓励学生大胆质疑,激发学生的好奇心和主动学习的欲望.
重点:列出一元一次方程解有关形积变化问题;依题意准确把握形积问题中的相等关系。
难点:一元一次方程解有关形积变化问题;依题意准确把握形积问题中的相等关系。
学法指导及使用说明:启发式教学
知识链接:
一、学习流程:1、用同一块橡皮泥捏出不同形状的几何体。(1)想想它有何变化?(2)你发现有什么相等关系?2.填空:长方形的周长=
面积=
长方体的体积=
正方体的体积=
圆的周长=
面积
=
圆柱的体积=
二、探究新知:探究点一:等体积的变化某居民楼顶有一个底面直径和高均为4m的圆柱形储水箱,现该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4m减少为3.2m,那么在容积不变的前提下,水箱的高度将由原先的4m增高为多少米?
假设在锻压过程中圆柱的体积保持不变,那么在这个问题中有如下的等量关系:
旧水箱的容积=新水箱的容积。解:设锻压后圆柱的高为x厘米,填写下表:旧水箱新水箱底面半径高体积
根据等量关系,列出方程:
(接着解方程)
答:水箱的高变成了
米。探究点二:等周长的变化1、用一根长为10米的铁丝围成一个长方形。(1)使得该长方形的长比宽多1.4米,此时长方形的长、宽各为多少米?面积为多少?解:设此时长方形的宽为
米,则它的长为
米。根据题意,得:(列方程并解方程)
它所围成的长方形的长为
此时所围成的长方形面积为:
(2)使得该长方形的长比宽多0.8米,此时长方形的长、宽各为多少米?它所围成的长方形与(1)中所围长方形相比,面积有什么变化?
解:设长方形的宽为
米,则它的长为
米。根据题意,得:(列方程并解方程)
它所围成的长方形的长为:
此时所围成的长方形面积为:
此时与(1)中所围成的长方形的面积相比,情况如何?(3)使得该长方形的长与宽相等,即围成一个正方形,此时正方形的边长是多少米?它所围成的面积与(2)中的长方形面积相比又有什么变化?解:设正方形的边长为
米。根据题意,得:(列方程并解方程)
此时所围成的正方形的面积为
此时与(2)中所围成的长方形的面积相比,情况如何?三、达标测评(1)圆柱的直径是8厘米,高6厘米,大圆柱的直径是10厘米,并且它的体积是小圆柱体体积的2.5倍,那么大圆柱的高是多少?
(2)墙上钉着用一根彩绳围成的梯形形状的饰物,如右图实线所示。小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如右图虚线所示。小颖所钉长方形的长、宽各为多少厘米?(3)将一个长、宽、高分别为15cm,12cm和8cm的长方形钢块锻造成一个底面边长为12cm的正方形的长方体零件钢坯,试问锻造前长方体的钢块表面积大还是锻造后的长方体零件钢坯表面积大?请你计算比较。(4)第一块试验田的面积比第一块试验田的面积的3倍还多100平方米,这两块试验田的面积共2900平方米,两块实验田的面积分别是多少?四、谈谈你的收获?五、你还有那些疑问?
备注(教师复备栏及学生笔记)
装
订
线
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
