必修一2.2.2.2对数函数性质的应用 同步训练(含答案)
文档属性
| 名称 | 必修一2.2.2.2对数函数性质的应用 同步训练(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 83.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-29 19:08:35 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
2.2.2.2 对数函数的性质应用 同步训练(含答案)
选择题
1.若集合M={x|logx≥},则 RM等于( )
A.(-∞,0]∪ B.
C.(-∞,0]∪ D.
2.设m=log3π,n=log2,p=log3,则( )
A.m>n>p B.m>p>n C.n>m>p D.n>p>m
3.函数y=log(-x2+4x+12)的单调递减区间是( )
A.(-∞,2) B.(2,+∞) C.(-2,2) D.(-2,6)
4.设函数f(x)=ln(1-x)-ln(1+x),则f(x)是( )
A.奇函数,且在(0,1)上是增函数 B.奇函数,且在(0,1)上是减函数
C.偶函数,且在(0,1)上是增函数 D.偶函数,且在(0,1)上是减函数
5.函数f(x)的图象如下图折线ACB,则使不等式f(x)≧log2(x+1)成立的x的取值范围是( )21cnjy.com
A. B. C. D.
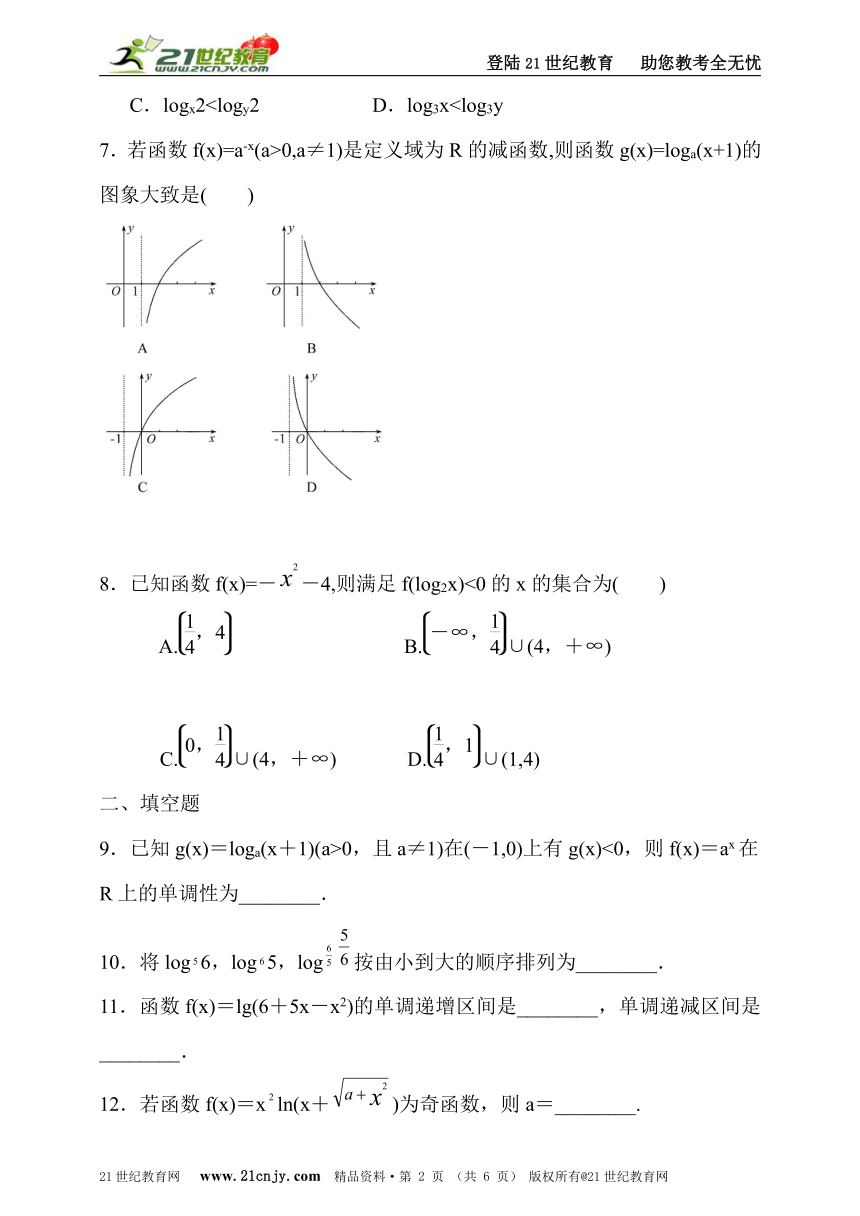
6.若0A.logx>logy B.xC.logx27.若函数f(x)=a-x(a>0,a≠1)是定义域为R的减函数,则函数g(x)=loga(x+1)的图象大致是( )21世纪教育网版权所有
8.已知函数f(x)=--4,则满足f(log2x)<0的x的集合为( )
A. B.∪(4,+∞)
C.∪(4,+∞) D.∪(1,4)
二、填空题
9.已知g(x)=loga(x+1)(a>0,且a≠1)在(-1,0)上有g(x)<0,则f(x)=ax在R上的单调性为________.【来源:21·世纪·教育·网】
10.将log6,log5,log按由小到大的顺序排列为________.
11.函数f(x)=lg(6+5x-x2)的单调递增区间是________,单调递减区间是________.【来源:21cnj*y.co*m】
12.若函数f(x)=xln(x+)为奇函数,则a=________.
13.若函数f(x)=(a>0,且a≠1)的值域是[3,+∞),则实数a的取值范围是________.【出处:21教育名师】
三、解答题
14.已知函数f(x)=(log2x)2-4log2x.
(1)求方程f(x)-5=0的解;
(2)当x∈时,求函数f(x)的最值,并求f(x)取最值时对应的x的值.
15.已知函数f(x)=的图象关于原点对称,其中a为常数.
(1)求a的值;
(2)若当x∈(2,+∞)时,f(x)+log(x-1)参考答案:
1.解析:logx≥,即logx≥log,∴0}.故选A.答案:Awww.21-cn-jy.com
2.解析:m=log3π>1,n=log2=log23∈.p=log3=log32∈,故有m>m>p.答案:A21教育网
3.解析:y=logu,u=-x2+4x+12.令u=-x2+4x+12>0,得-24.解析:f(x)=ln,f(x)=ln(-1+),易知f(x)在(0,1)是减函数,又定义域是(-1,1),且f(-x)=ln(1+x)-ln(1-x)=-f(x),故f(x)为奇函数,选B.答案:Bwww-2-1-cnjy-com
5.解析:在平面直角坐标系中作出函数y=log2(x+1)的图象如图所示.
所以f(x)≥log2(x+1)的解集是,所以选C.答案:C
6.解析:∵y=log2x是增函数,∴当x∵y=logx是减函数,∴当xlogy.∵log2x∴.∴logy27.解析:由函数f(x)=a-x(a>0,a≠1)是定义域为R的减函数可知,a>1,结合左加右减可得C正确,答案:C2-1-c-n-j-y
8.解析:因为f(x)为偶函数,且在[0,+∞)上递减,又f(2)=0,所以f(log2x)<0时,应有log2x>2或log2x<-2,解得x>4或08.答案:C
9.解析:∵x∈(-1,0),∴x+1∈(0,1),又x∈(-1,0)时,g(x)<0.∴a>1,∴f(x)=ax在R上是增函数.答案:单调递增【版权所有:21教育】
10.解析:∵log6>log5=1,011.解析:∵6+5x-x2>0,∴x2-5x-6<0.∴-1同理,函数f(x)=ln(6+5x-x2)的单调递减区间是(,5).答案:(-1,) (,5)
12.解析:由题意得f(x)=xln(x+)是奇函数,
=f(-x)=-xln(-x),g(x)=ln(x+)必然是奇函数,所以g(0)=0,带入解得a=1.答案:12·1·c·n·j·y
13.解析:当x≤2时,f(x)≥3;又函数f(x)的值域为[3,+∞),
所以解得114.解:(1)∵f(x)-5=0.∴(log2x)2-4log2x-5=0.∴(log2x-5)(log2x+1)=0,∴log2x=5或log2x=-1,∴x=32或.21*cnjy*com
(2)设t=log2x,∵x∈,∴t∈[-1,3]f(x)=t2-4t=(t-2)2-16.
当t=2时,x=4,f(x)min=-16,当t=-1时,x=,f(x)max=5.
15.解:(1)因为函数f(x)的图象关于原点对称,所以函数f(x)为奇函数,故f(-x)=-f(x),即log=-log=log,
所以=>0,解得a=-1或a=1(舍去).
(2)f(x)+(x-1)=+log(x-1)=log(x+1),
当x∈(2,+∞)时,x+1∈(3,+∞).所以log(x+1)<3=-1.由已知不等式恒成立可得t≥-1.故实数t的取值范围为[-1,+∞).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 1 页) 版权所有@21世纪教育网
2.2.2.2 对数函数的性质应用 同步训练(含答案)
选择题
1.若集合M={x|logx≥},则 RM等于( )
A.(-∞,0]∪ B.
C.(-∞,0]∪ D.
2.设m=log3π,n=log2,p=log3,则( )
A.m>n>p B.m>p>n C.n>m>p D.n>p>m
3.函数y=log(-x2+4x+12)的单调递减区间是( )
A.(-∞,2) B.(2,+∞) C.(-2,2) D.(-2,6)
4.设函数f(x)=ln(1-x)-ln(1+x),则f(x)是( )
A.奇函数,且在(0,1)上是增函数 B.奇函数,且在(0,1)上是减函数
C.偶函数,且在(0,1)上是增函数 D.偶函数,且在(0,1)上是减函数
5.函数f(x)的图象如下图折线ACB,则使不等式f(x)≧log2(x+1)成立的x的取值范围是( )21cnjy.com
A. B. C. D.
6.若0
8.已知函数f(x)=--4,则满足f(log2x)<0的x的集合为( )
A. B.∪(4,+∞)
C.∪(4,+∞) D.∪(1,4)
二、填空题
9.已知g(x)=loga(x+1)(a>0,且a≠1)在(-1,0)上有g(x)<0,则f(x)=ax在R上的单调性为________.【来源:21·世纪·教育·网】
10.将log6,log5,log按由小到大的顺序排列为________.
11.函数f(x)=lg(6+5x-x2)的单调递增区间是________,单调递减区间是________.【来源:21cnj*y.co*m】
12.若函数f(x)=xln(x+)为奇函数,则a=________.
13.若函数f(x)=(a>0,且a≠1)的值域是[3,+∞),则实数a的取值范围是________.【出处:21教育名师】
三、解答题
14.已知函数f(x)=(log2x)2-4log2x.
(1)求方程f(x)-5=0的解;
(2)当x∈时,求函数f(x)的最值,并求f(x)取最值时对应的x的值.
15.已知函数f(x)=的图象关于原点对称,其中a为常数.
(1)求a的值;
(2)若当x∈(2,+∞)时,f(x)+log(x-1)
1.解析:logx≥,即logx≥log,∴0
2.解析:m=log3π>1,n=log2=log23∈.p=log3=log32∈,故有m>m>p.答案:A21教育网
3.解析:y=logu,u=-x2+4x+12.令u=-x2+4x+12>0,得-2
5.解析:在平面直角坐标系中作出函数y=log2(x+1)的图象如图所示.
所以f(x)≥log2(x+1)的解集是,所以选C.答案:C
6.解析:∵y=log2x是增函数,∴当x
8.解析:因为f(x)为偶函数,且在[0,+∞)上递减,又f(2)=0,所以f(log2x)<0时,应有log2x>2或log2x<-2,解得x>4或0
9.解析:∵x∈(-1,0),∴x+1∈(0,1),又x∈(-1,0)时,g(x)<0.∴a>1,∴f(x)=ax在R上是增函数.答案:单调递增【版权所有:21教育】
10.解析:∵log6>log5=1,0
12.解析:由题意得f(x)=xln(x+)是奇函数,
=f(-x)=-xln(-x),g(x)=ln(x+)必然是奇函数,所以g(0)=0,带入解得a=1.答案:12·1·c·n·j·y
13.解析:当x≤2时,f(x)≥3;又函数f(x)的值域为[3,+∞),
所以解得1
(2)设t=log2x,∵x∈,∴t∈[-1,3]f(x)=t2-4t=(t-2)2-16.
当t=2时,x=4,f(x)min=-16,当t=-1时,x=,f(x)max=5.
15.解:(1)因为函数f(x)的图象关于原点对称,所以函数f(x)为奇函数,故f(-x)=-f(x),即log=-log=log,
所以=>0,解得a=-1或a=1(舍去).
(2)f(x)+(x-1)=+log(x-1)=log(x+1),
当x∈(2,+∞)时,x+1∈(3,+∞).所以log(x+1)<3=-1.由已知不等式恒成立可得t≥-1.故实数t的取值范围为[-1,+∞).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 1 页) 版权所有@21世纪教育网
