直线与直线的位置关系
图片预览


文档简介
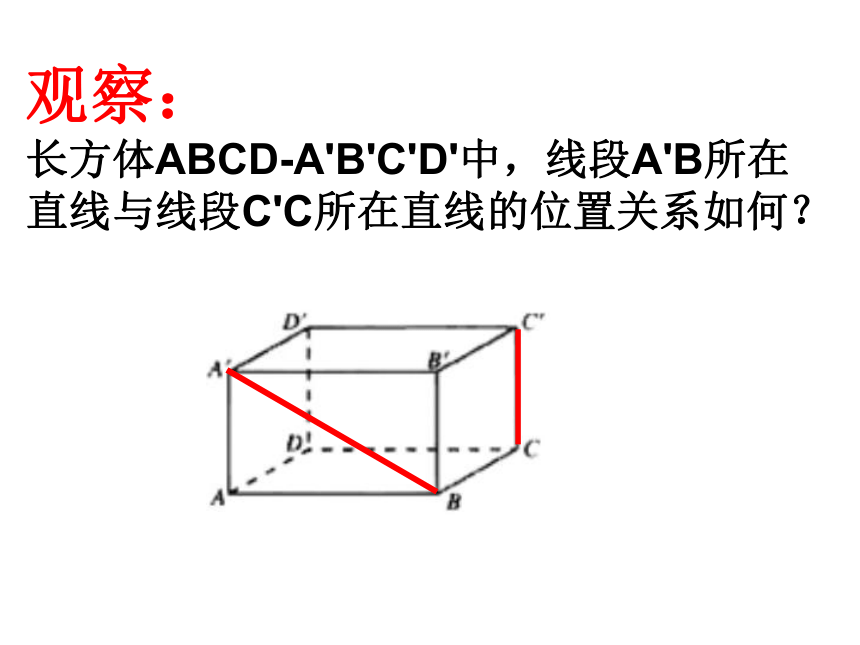
课件24张PPT。空间中直线与直线的位置关系观察:
长方体ABCD-A'B'C'D'中,线段A'B所在
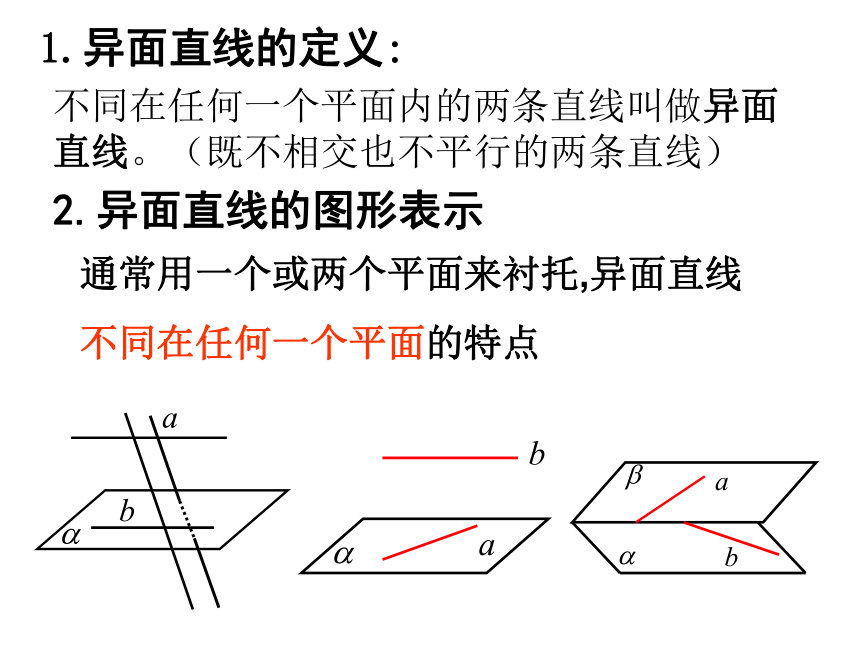
直线与线段C'C所在直线的位置关系如何?1.异面直线的定义:2.异面直线的图形表示不同在任何一个平面内的两条直线叫做异面直线。(既不相交也不平行的两条直线)通常用一个或两个平面来衬托,异面直线
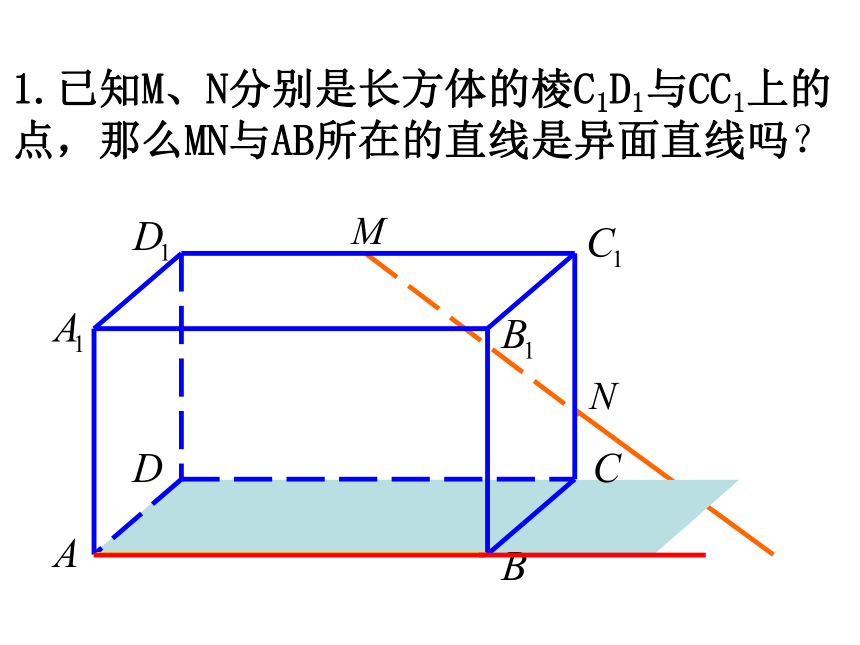
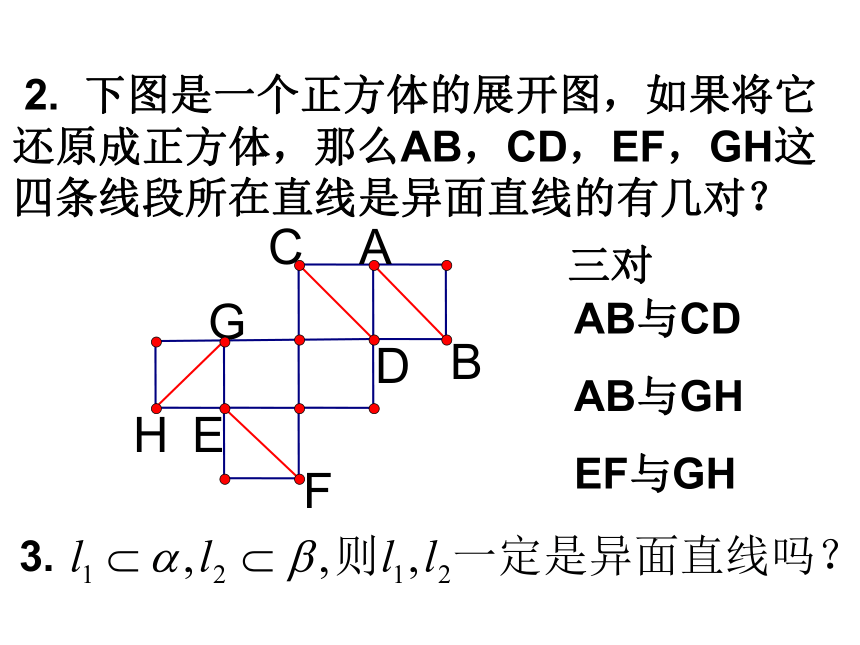
不同在任何一个平面的特点1.已知M、N分别是长方体的棱C1D1与CC1上的点,那么MN与AB所在的直线是异面直线吗? 2. 下图是一个正方体的展开图,如果将它还原成正方体,那么AB,CD,EF,GH这四条线段所在直线是异面直线的有几对?三对AB与CD
AB与GH
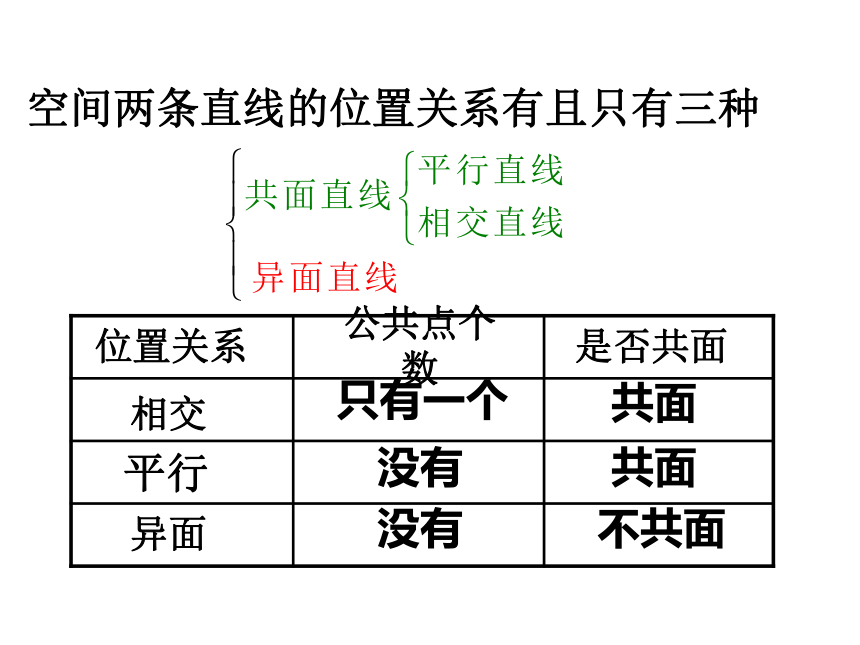
EF与GH3.空间两条直线的位置关系有且只有三种没有只有一个没有共面不共面共面公理4:平行于同一条直线的两条直线互相平行。a∥b
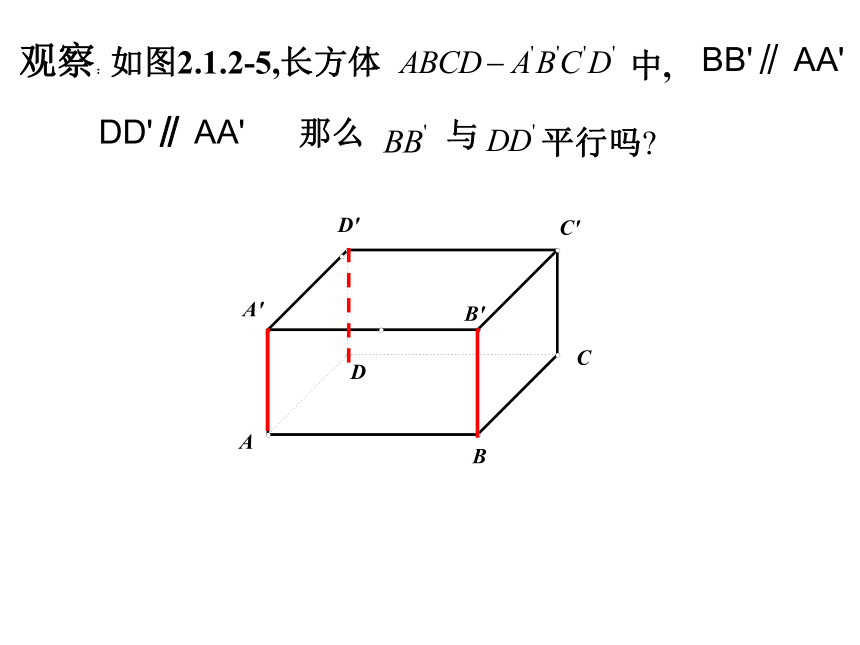
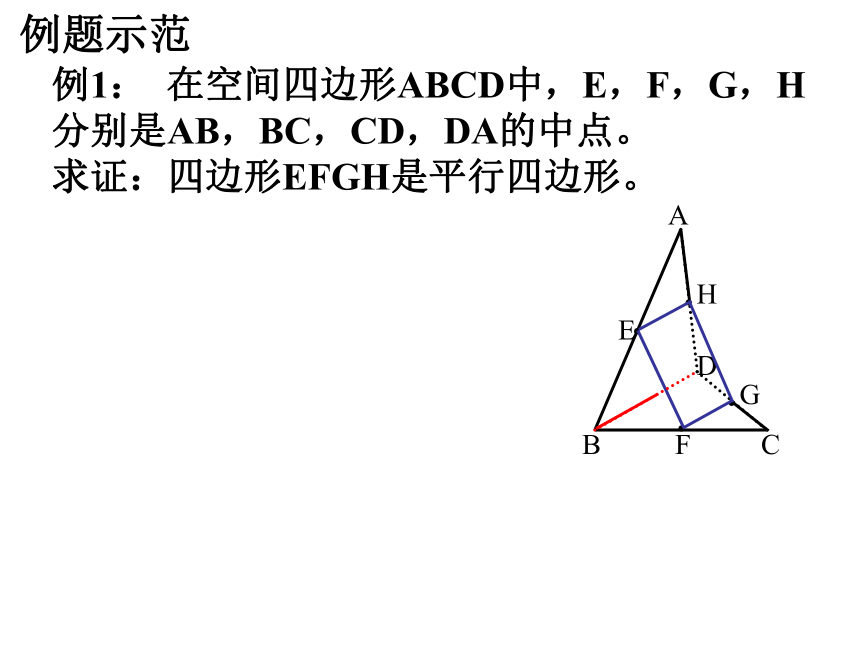
c∥ba∥c符号表示:设空间中的三条直线分别为a, b, c,若想一想:空间中,如果两条直线都与第三条直线垂直,是否也有类似的规律?例题示范例1: 在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形。变式一: 在例2中,如果再加上条件AC=BD,那么四边形EFGH是什么图形? EHFG菱形变式二: 空间四面体A--BCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD上的点,且 ,
求证:四边形ABCD为梯形.ABCDEHFG3.?等角定理观察思考:如图,∠ADC与∠A'D'C'、∠ADC与∠A'B'C'的两边分别对应平行,这两组角的大小关系如何?3.?等角定理定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。三、两条异面直线所成的角如图所示,a,b是两条异面直线,在空间中任选一点O,过O点分别作 a,b的平行线 a′和 b′,a′b′ 则这两条线所成的锐角θ(或直角),θ 称为异面直线a,b所成的角。?任选若两条异面直线所成角为90°,则称它们互相垂直。异面直线a与b垂直也记作a⊥b异面直线所成角θ的取值范围: 平移例题示范例2、如图,已知正方体ABCD-A'B'C'D'?中。
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'?和CC'?的夹角是多少?
(3)哪些棱所在的直线与直线AA'?垂直?,例3:?如图, 是平面 外的一点 分别是
的重心,
求证: 。 证明:连结 分别交
于 ,连结 ,
∵G,H分别是⊿ABC,⊿ACD的重心,∴M,N分别是BC,CD的中点,
∴MN//BD,
又∵
∴ GH//MN,由公理4知GH//BD.
【例1】如图正方体中,E、F分别为D1C1和B1C1的中点,P、Q分别为AC与BD、A1C1与EF的交点.
(1)求证:D、B、F、E四点共面;
(2)若A1C与面DBFE交于点R,
求证:P、Q、R三点共线.练习【例2】如图中,正方体ABCD—A1B1C1D1,E、F分别是AD、AA1的中点.
(1)求直线AB1和CC1所成的角的大小;
(2)求直线AB1和EF所成的角的大小.练习反馈:1. 判断:
(1)平行于同一直线的两条直线平行.( )
(2)垂直于同一直线的两条直线平行.( ?)
(3)过直线外一点,有且只有一条直线与已知直线平行?.?( )
(4)与已知直线平行且距离等于定长的直线只有两条.???( )
(5)若一个角的两边分别与另一个角的两边平行,那么这两个角相等( )
(6)若两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.?(???)????√×√√××练习反馈:2.选择题
?(1)“a,b是异面直线”是指?①?a∩b=Φ,且a不平行于b;②?a ì平面a,bì平面b且a∩b=Φ ③?a?ì平面a,b??平面a?④?不存在平面a,能使a?ìa且b?ìa成立
上述结论中,正确的是 (???)
(A)①② (B)①③ (C)①④ (D)③④(2)长方体的一条对角线与长方体的棱所组成的异面直线有 (???)
?(A)2对 (B)3对 (C)6对 (D)12对CC(3)两条直线a,b分别和异面直线c,d都相交,则直线a,b的位置关系是(??)
?(A)一定是异面直线 (B)一定是相交直线
?(C)可能是平行直线
(D)可能是异面直线,也可能是相交直线
(4)一条直线和两条异面直线中的一条平行,则它和另一条的位置关系是(? )
(A)平行 (B)相交
(C)异面 (D)相交或异面3.两条直线互相垂直,它们一定相交吗????答:不一定,还可能异面.DD4.垂直于同一直线的两条直线,有几种位置关系?答:三种:相交,平行,异面.5.画两个相交平面,在这两个平面内各画一条直线使它们成为(1)平行直线;(2)相交直线;(3)异面直线.6.选择题
?(1)分别在两个平面内的两条直线间的位置关系是 (? )
?(A)异面 (B)平行
(C)相交 (D)以上都有可能??
(2)异面直线a,b满足a?ìa,b?ìb,a∩b=l,
则l与a,b的位置关系一定是(? )(A)l至多与a,b中的一条相交;
(B)l至少与a,b中的一条相交;
(C)l与a,b都相交;
(D)l至少与a,b中的一条平行.DB(3)两异面直线所成的角的范围是 ( )
(A)(0°,90°) (B)[0°,90°)
(C)(0°,90°] (D)[0°,90°]7.判断下列命题的真假,真的打“√”,假的打“×”
?(1)两条直线和第三条直线成等角,则这两条直线平行???????????(???)
?(2)平行移动两条异面直线中的任一条,它们所成的角不变???????(??)
?(3)四边相等且四个角也相等的四边形是正方形?????????????????(???)C×√×
长方体ABCD-A'B'C'D'中,线段A'B所在
直线与线段C'C所在直线的位置关系如何?1.异面直线的定义:2.异面直线的图形表示不同在任何一个平面内的两条直线叫做异面直线。(既不相交也不平行的两条直线)通常用一个或两个平面来衬托,异面直线
不同在任何一个平面的特点1.已知M、N分别是长方体的棱C1D1与CC1上的点,那么MN与AB所在的直线是异面直线吗? 2. 下图是一个正方体的展开图,如果将它还原成正方体,那么AB,CD,EF,GH这四条线段所在直线是异面直线的有几对?三对AB与CD
AB与GH
EF与GH3.空间两条直线的位置关系有且只有三种没有只有一个没有共面不共面共面公理4:平行于同一条直线的两条直线互相平行。a∥b
c∥ba∥c符号表示:设空间中的三条直线分别为a, b, c,若想一想:空间中,如果两条直线都与第三条直线垂直,是否也有类似的规律?例题示范例1: 在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形。变式一: 在例2中,如果再加上条件AC=BD,那么四边形EFGH是什么图形? EHFG菱形变式二: 空间四面体A--BCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD上的点,且 ,
求证:四边形ABCD为梯形.ABCDEHFG3.?等角定理观察思考:如图,∠ADC与∠A'D'C'、∠ADC与∠A'B'C'的两边分别对应平行,这两组角的大小关系如何?3.?等角定理定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。三、两条异面直线所成的角如图所示,a,b是两条异面直线,在空间中任选一点O,过O点分别作 a,b的平行线 a′和 b′,a′b′ 则这两条线所成的锐角θ(或直角),θ 称为异面直线a,b所成的角。?任选若两条异面直线所成角为90°,则称它们互相垂直。异面直线a与b垂直也记作a⊥b异面直线所成角θ的取值范围: 平移例题示范例2、如图,已知正方体ABCD-A'B'C'D'?中。
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'?和CC'?的夹角是多少?
(3)哪些棱所在的直线与直线AA'?垂直?,例3:?如图, 是平面 外的一点 分别是
的重心,
求证: 。 证明:连结 分别交
于 ,连结 ,
∵G,H分别是⊿ABC,⊿ACD的重心,∴M,N分别是BC,CD的中点,
∴MN//BD,
又∵
∴ GH//MN,由公理4知GH//BD.
【例1】如图正方体中,E、F分别为D1C1和B1C1的中点,P、Q分别为AC与BD、A1C1与EF的交点.
(1)求证:D、B、F、E四点共面;
(2)若A1C与面DBFE交于点R,
求证:P、Q、R三点共线.练习【例2】如图中,正方体ABCD—A1B1C1D1,E、F分别是AD、AA1的中点.
(1)求直线AB1和CC1所成的角的大小;
(2)求直线AB1和EF所成的角的大小.练习反馈:1. 判断:
(1)平行于同一直线的两条直线平行.( )
(2)垂直于同一直线的两条直线平行.( ?)
(3)过直线外一点,有且只有一条直线与已知直线平行?.?( )
(4)与已知直线平行且距离等于定长的直线只有两条.???( )
(5)若一个角的两边分别与另一个角的两边平行,那么这两个角相等( )
(6)若两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.?(???)????√×√√××练习反馈:2.选择题
?(1)“a,b是异面直线”是指?①?a∩b=Φ,且a不平行于b;②?a ì平面a,bì平面b且a∩b=Φ ③?a?ì平面a,b??平面a?④?不存在平面a,能使a?ìa且b?ìa成立
上述结论中,正确的是 (???)
(A)①② (B)①③ (C)①④ (D)③④(2)长方体的一条对角线与长方体的棱所组成的异面直线有 (???)
?(A)2对 (B)3对 (C)6对 (D)12对CC(3)两条直线a,b分别和异面直线c,d都相交,则直线a,b的位置关系是(??)
?(A)一定是异面直线 (B)一定是相交直线
?(C)可能是平行直线
(D)可能是异面直线,也可能是相交直线
(4)一条直线和两条异面直线中的一条平行,则它和另一条的位置关系是(? )
(A)平行 (B)相交
(C)异面 (D)相交或异面3.两条直线互相垂直,它们一定相交吗????答:不一定,还可能异面.DD4.垂直于同一直线的两条直线,有几种位置关系?答:三种:相交,平行,异面.5.画两个相交平面,在这两个平面内各画一条直线使它们成为(1)平行直线;(2)相交直线;(3)异面直线.6.选择题
?(1)分别在两个平面内的两条直线间的位置关系是 (? )
?(A)异面 (B)平行
(C)相交 (D)以上都有可能??
(2)异面直线a,b满足a?ìa,b?ìb,a∩b=l,
则l与a,b的位置关系一定是(? )(A)l至多与a,b中的一条相交;
(B)l至少与a,b中的一条相交;
(C)l与a,b都相交;
(D)l至少与a,b中的一条平行.DB(3)两异面直线所成的角的范围是 ( )
(A)(0°,90°) (B)[0°,90°)
(C)(0°,90°] (D)[0°,90°]7.判断下列命题的真假,真的打“√”,假的打“×”
?(1)两条直线和第三条直线成等角,则这两条直线平行???????????(???)
?(2)平行移动两条异面直线中的任一条,它们所成的角不变???????(??)
?(3)四边相等且四个角也相等的四边形是正方形?????????????????(???)C×√×
