广东省珠海市2009-2010学年度第一学期期末学生学业质量监测(数学文)
文档属性
| 名称 | 广东省珠海市2009-2010学年度第一学期期末学生学业质量监测(数学文) |  | |
| 格式 | zip | ||
| 文件大小 | 162.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-15 14:57:00 | ||
图片预览



文档简介
高考资源网( www.),您身边的高考专家
高考资源网( www.),您身边的高考专家
珠海市2009---2010学年度第一学期期末学生学业质量监测
高三文科数学试卷
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,且
A. B. C. D.
2.若函数,则下面必在反函数图像上的点是
A. B.
C. D.
3.右图为某几何体三视图,按图中所给数据,该几何体的体积为
A.64+16 B. 16+
C.16 D. 16
4.在各项都为正数的等比数列中,首项为3,前3项和为
21,则( )
A.33 B.72 C.84 D.189
5. 将函数的图像向右平移个单位后所得的图像的一个对称轴是:
A. B. C. D.
6. 若以连续抛掷两次骰子分别得到的点数m,n作为点P的坐标,则点P落在圆 内(含边界)的概率为
A. B. C. D.
7.下列有关命题的说法正确的是
A.“”是“”的充分不必要条件
B.“”是“”的必要不充分条件.
C.命题“使得”的否定是:“ 均有”.
D.命题“若,则”的逆否命题为真命题.
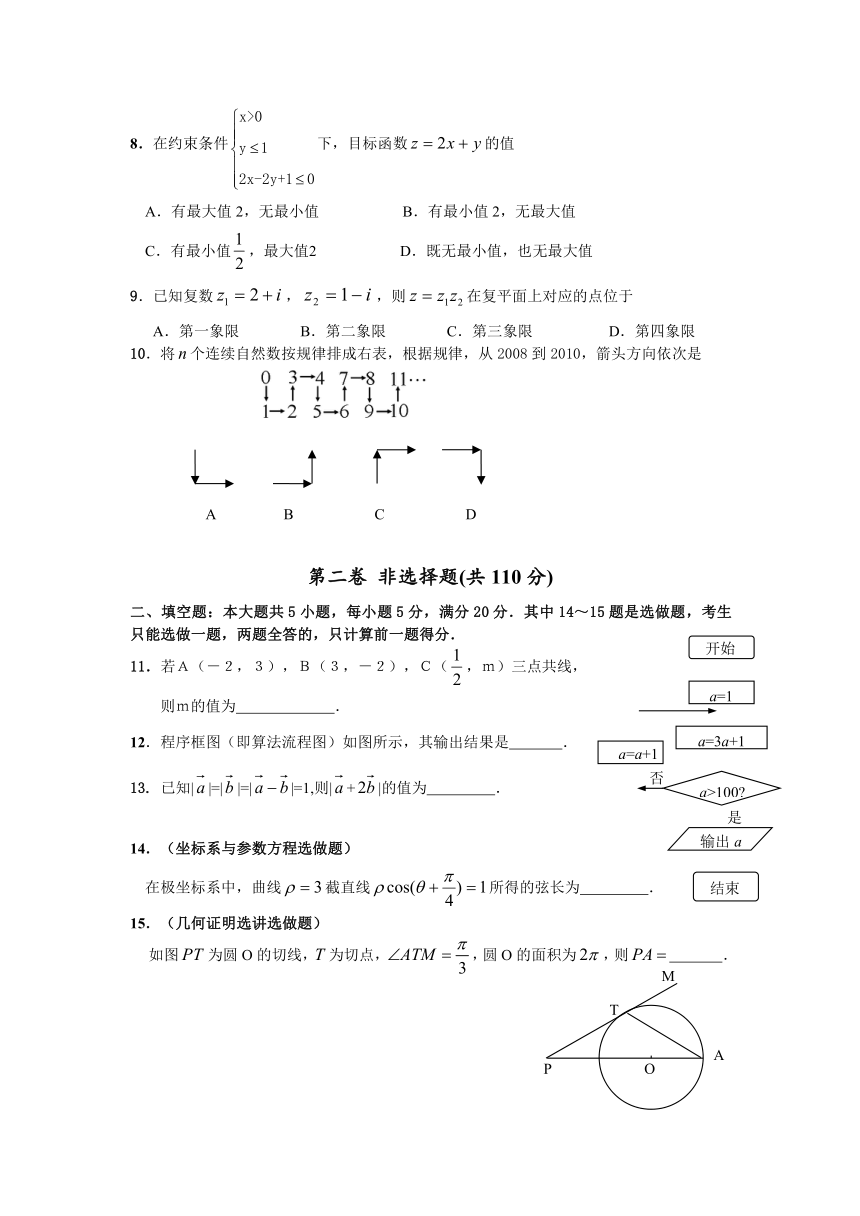
8.在约束条件下,目标函数的值
A.有最大值2,无最小值 B.有最小值2,无最大值
C.有最小值,最大值2 D.既无最小值,也无最大值
9.已知复数,,则在复平面上对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.将个连续自然数按规律排成右表,根据规律,从2008到2010,箭头方向依次是
第二卷 非选择题(共110分)
二、填空题:本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.
11.若A(-2,3),B(3,-2),C(,m)三点共线,
则m的值为 .
12.程序框图(即算法流程图)如图所示,其输出结果是 .
13. 已知||=||=||=1,则|+|的值为 .
14.(坐标系与参数方程选做题)
在极坐标系中,曲线截直线所得的弦长为 .
15.(几何证明选讲选做题)
如图为圆O的切线,为切点,,圆O的面积为,则 .
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
已知,
⑴ 求的最大值及此时的值;
⑵ 求在定义域上的单调递增区间。
17.(本小题满分12分)
型号 甲样式 乙样式 丙样式
500ml 2000 z 3000
700ml 3000 4500 5000
一工厂生产甲, 乙, 丙三种样式的杯子,每种样式均有500ml和700ml两种型号,某天的产量如右表(单位:个):
按样式分层抽样的方法在这个月生产的杯子中抽取100个,其中有甲样式杯子25个.
求z的值;
用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本,从这个样本中任取2个杯子,求至少有1个500ml杯子的概率.
18.(本小题满分14分)
如图,已知⊥平面,∥,=2,且是的中点.
(Ⅰ)求证:∥平面;
(Ⅱ)求证:平面BCE⊥平面;
(III)求此多面体的体积.
19.(本小题满分14分)
设椭圆的左右焦点分别为、,是椭圆上的一点,,坐标原点到直线的距离为.
(1)求椭圆的方程;
(2)设是椭圆上的一点,,连接QN的直线交轴于点,若,求直线的斜率.
20.(本小题满分14分)
已知函数.
(1)当时,证明函数只有一个零点;
(2)若函数在区间上是减函数,求实数 ( http: / / www.21cnjy.com / )的取值范围.
21. (本小题满分14分)
已知数列中, .
(1)求数列的通项公式;
(2)设: 求数列的前项的和;
(3)已知,求证:.
珠海市2009---2010学年度第一学期期末学生学业质量监测
高三文科数学试卷(答案及评分标准)
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. C 2. C 3. B 4. C 5.A 6. A 7.D 8. A 9.D 10.A
二、填空题:本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.
11. 12. 160 13. 14. 15.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
解:⑴ -----------3分
当时,即时, -----------6分
⑵由得
在定义域上的单调递增区间 -----------12分
17.(本小题满分12分)
解: (1).设该厂本月生产的乙样式的杯子为n个,在丙样式的杯子中抽取x个,由题意得,
,所以x=40. -----------2分
则100-40-25=35,所以,
n=7000,
故z=2500 ----------6分
(2) 设所抽样本中有m个500ml杯子,
因为用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本,
所以,解得m=2 -----------9分
也就是抽取了2个500ml杯子,3个700ml杯子,
分别记作S1,S2;B1,B2,B3,则从中任取2个的所有基本事 ( http: / / www.21cnjy.com / )件为
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)
共10个,其中至少有1个500ml杯子的基本事件有7个基本事件:
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),所以从中任取2个,
至少有1个500ml杯子的概率为. -----------12分
18.(本小题满分14分),
解:(Ⅰ)取CE中点P,连结FP、BP,
∵F为CD的中点,
∴FP∥DE,且FP=
又AB∥DE,且AB=
∴AB∥FP,且AB=FP,
∴ABPF为平行四边形,∴AF∥BP. …………3分
又∵AF平面BCE,BP平面BCE,
∴AF∥平面BCE …………5分
(Ⅱ)∵,所以△ACD为正三角形,∴AF⊥CD
∵AB⊥平面ACD,DE//AB
∴DE⊥平面ACD 又AF平面ACD
∴DE⊥AF
又AF⊥CD,CD∩DE=D
∴AF⊥平面CDE …………8分
又BP∥AF ∴BP⊥平面CDE
又∵BP平面BCE
∴平面BCE⊥平面CDE …………10分
(III)此多面体是一个以C为定点,以四边形ABED为底边的四棱锥,
,等边三角形AD边上的高就是四棱锥的高
…………14分
19.(本小题满分14分)
解:(1)由题设知
由于,则有,所以点的坐标为
故所在直线方程为
所以坐标原点到直线的距离为
又,所以 解得:
所求椭圆的方程为 -----------7分
(2)由题意可知直线的斜率存在,设直线斜率为直线的方程为,则有 设,由于、N、三点共线,且
根据题意得,解得或
又在椭圆上,故或
解得,综上,直线的斜率为或.-----------14分
20.(本小题满分14分)函数
解:(Ⅰ)当时,,其定义域是
∴ …………2分
令,即,解得或.,
∴ 舍去.
当时,;当时,.
∴ 函数在区间上单调递增,在区间上单调递减
∴ 当x =1时,函数取得最大值,其值为.
当时,,即.
∴ 函数只有一个零点. ……………7分
(Ⅱ)显然函数的定义域为
∴ ………8分
当时,在区间上为增函数,不合题意……9分
当时,等价于,即
此时的单调递减区间为.
依题意,得解之得. ………11分
综上,实数的取值范围是 ………14分
法二:
①当时,在区间上为增函数,不合题意……9分
②当时,要使函数在区间上是减函数,只需在区间上恒成立,只要,且时恒成立,
解得
综上,实数的取值范围是 …………14分
21. (本小题满分14分)
解:(1)由得:且,
所以知:数列是以1为首项,以2为公差的等差数列, …………2分
所以 ; ------------4分
(2)由得: ,
从而: ------------6分
则
=
------------9分
(3)已知
设:,则
从而:
故: ------------14分
A
B
C
D
开始
a=1
a=a+1
a=3a+1
否
a>100
输出a
是
结束
P
T
M
A
O
A
B
C
D
E
F
(18题图)
欢迎广大教师踊跃来稿。 www.
欢迎广大教师踊跃来稿。 www.
高考资源网( www.),您身边的高考专家
珠海市2009---2010学年度第一学期期末学生学业质量监测
高三文科数学试卷
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,且
A. B. C. D.
2.若函数,则下面必在反函数图像上的点是
A. B.
C. D.
3.右图为某几何体三视图,按图中所给数据,该几何体的体积为
A.64+16 B. 16+
C.16 D. 16
4.在各项都为正数的等比数列中,首项为3,前3项和为
21,则( )
A.33 B.72 C.84 D.189
5. 将函数的图像向右平移个单位后所得的图像的一个对称轴是:
A. B. C. D.
6. 若以连续抛掷两次骰子分别得到的点数m,n作为点P的坐标,则点P落在圆 内(含边界)的概率为
A. B. C. D.
7.下列有关命题的说法正确的是
A.“”是“”的充分不必要条件
B.“”是“”的必要不充分条件.
C.命题“使得”的否定是:“ 均有”.
D.命题“若,则”的逆否命题为真命题.
8.在约束条件下,目标函数的值
A.有最大值2,无最小值 B.有最小值2,无最大值
C.有最小值,最大值2 D.既无最小值,也无最大值
9.已知复数,,则在复平面上对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.将个连续自然数按规律排成右表,根据规律,从2008到2010,箭头方向依次是
第二卷 非选择题(共110分)
二、填空题:本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.
11.若A(-2,3),B(3,-2),C(,m)三点共线,
则m的值为 .
12.程序框图(即算法流程图)如图所示,其输出结果是 .
13. 已知||=||=||=1,则|+|的值为 .
14.(坐标系与参数方程选做题)
在极坐标系中,曲线截直线所得的弦长为 .
15.(几何证明选讲选做题)
如图为圆O的切线,为切点,,圆O的面积为,则 .
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
已知,
⑴ 求的最大值及此时的值;
⑵ 求在定义域上的单调递增区间。
17.(本小题满分12分)
型号 甲样式 乙样式 丙样式
500ml 2000 z 3000
700ml 3000 4500 5000
一工厂生产甲, 乙, 丙三种样式的杯子,每种样式均有500ml和700ml两种型号,某天的产量如右表(单位:个):
按样式分层抽样的方法在这个月生产的杯子中抽取100个,其中有甲样式杯子25个.
求z的值;
用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本,从这个样本中任取2个杯子,求至少有1个500ml杯子的概率.
18.(本小题满分14分)
如图,已知⊥平面,∥,=2,且是的中点.
(Ⅰ)求证:∥平面;
(Ⅱ)求证:平面BCE⊥平面;
(III)求此多面体的体积.
19.(本小题满分14分)
设椭圆的左右焦点分别为、,是椭圆上的一点,,坐标原点到直线的距离为.
(1)求椭圆的方程;
(2)设是椭圆上的一点,,连接QN的直线交轴于点,若,求直线的斜率.
20.(本小题满分14分)
已知函数.
(1)当时,证明函数只有一个零点;
(2)若函数在区间上是减函数,求实数 ( http: / / www.21cnjy.com / )的取值范围.
21. (本小题满分14分)
已知数列中, .
(1)求数列的通项公式;
(2)设: 求数列的前项的和;
(3)已知,求证:.
珠海市2009---2010学年度第一学期期末学生学业质量监测
高三文科数学试卷(答案及评分标准)
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. C 2. C 3. B 4. C 5.A 6. A 7.D 8. A 9.D 10.A
二、填空题:本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.
11. 12. 160 13. 14. 15.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
解:⑴ -----------3分
当时,即时, -----------6分
⑵由得
在定义域上的单调递增区间 -----------12分
17.(本小题满分12分)
解: (1).设该厂本月生产的乙样式的杯子为n个,在丙样式的杯子中抽取x个,由题意得,
,所以x=40. -----------2分
则100-40-25=35,所以,
n=7000,
故z=2500 ----------6分
(2) 设所抽样本中有m个500ml杯子,
因为用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本,
所以,解得m=2 -----------9分
也就是抽取了2个500ml杯子,3个700ml杯子,
分别记作S1,S2;B1,B2,B3,则从中任取2个的所有基本事 ( http: / / www.21cnjy.com / )件为
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)
共10个,其中至少有1个500ml杯子的基本事件有7个基本事件:
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),所以从中任取2个,
至少有1个500ml杯子的概率为. -----------12分
18.(本小题满分14分),
解:(Ⅰ)取CE中点P,连结FP、BP,
∵F为CD的中点,
∴FP∥DE,且FP=
又AB∥DE,且AB=
∴AB∥FP,且AB=FP,
∴ABPF为平行四边形,∴AF∥BP. …………3分
又∵AF平面BCE,BP平面BCE,
∴AF∥平面BCE …………5分
(Ⅱ)∵,所以△ACD为正三角形,∴AF⊥CD
∵AB⊥平面ACD,DE//AB
∴DE⊥平面ACD 又AF平面ACD
∴DE⊥AF
又AF⊥CD,CD∩DE=D
∴AF⊥平面CDE …………8分
又BP∥AF ∴BP⊥平面CDE
又∵BP平面BCE
∴平面BCE⊥平面CDE …………10分
(III)此多面体是一个以C为定点,以四边形ABED为底边的四棱锥,
,等边三角形AD边上的高就是四棱锥的高
…………14分
19.(本小题满分14分)
解:(1)由题设知
由于,则有,所以点的坐标为
故所在直线方程为
所以坐标原点到直线的距离为
又,所以 解得:
所求椭圆的方程为 -----------7分
(2)由题意可知直线的斜率存在,设直线斜率为直线的方程为,则有 设,由于、N、三点共线,且
根据题意得,解得或
又在椭圆上,故或
解得,综上,直线的斜率为或.-----------14分
20.(本小题满分14分)函数
解:(Ⅰ)当时,,其定义域是
∴ …………2分
令,即,解得或.,
∴ 舍去.
当时,;当时,.
∴ 函数在区间上单调递增,在区间上单调递减
∴ 当x =1时,函数取得最大值,其值为.
当时,,即.
∴ 函数只有一个零点. ……………7分
(Ⅱ)显然函数的定义域为
∴ ………8分
当时,在区间上为增函数,不合题意……9分
当时,等价于,即
此时的单调递减区间为.
依题意,得解之得. ………11分
综上,实数的取值范围是 ………14分
法二:
①当时,在区间上为增函数,不合题意……9分
②当时,要使函数在区间上是减函数,只需在区间上恒成立,只要,且时恒成立,
解得
综上,实数的取值范围是 …………14分
21. (本小题满分14分)
解:(1)由得:且,
所以知:数列是以1为首项,以2为公差的等差数列, …………2分
所以 ; ------------4分
(2)由得: ,
从而: ------------6分
则
=
------------9分
(3)已知
设:,则
从而:
故: ------------14分
A
B
C
D
开始
a=1
a=a+1
a=3a+1
否
a>100
输出a
是
结束
P
T
M
A
O
A
B
C
D
E
F
(18题图)
欢迎广大教师踊跃来稿。 www.
欢迎广大教师踊跃来稿。 www.
同课章节目录
