三角形的外角

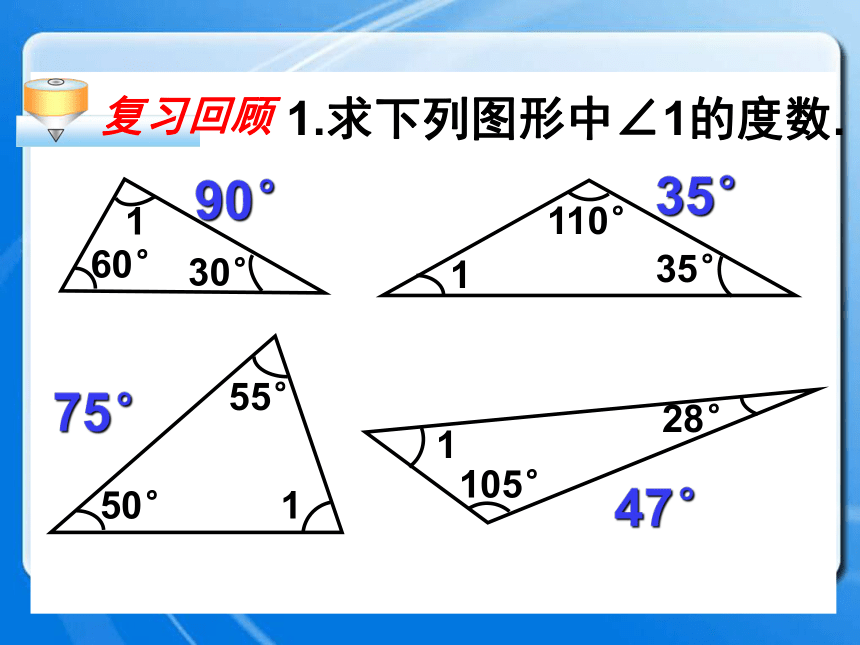
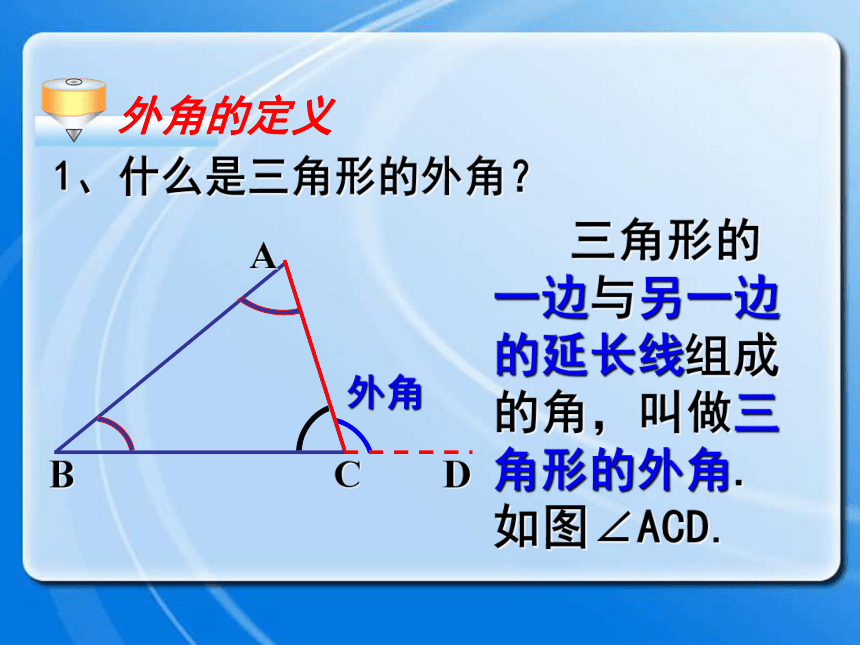
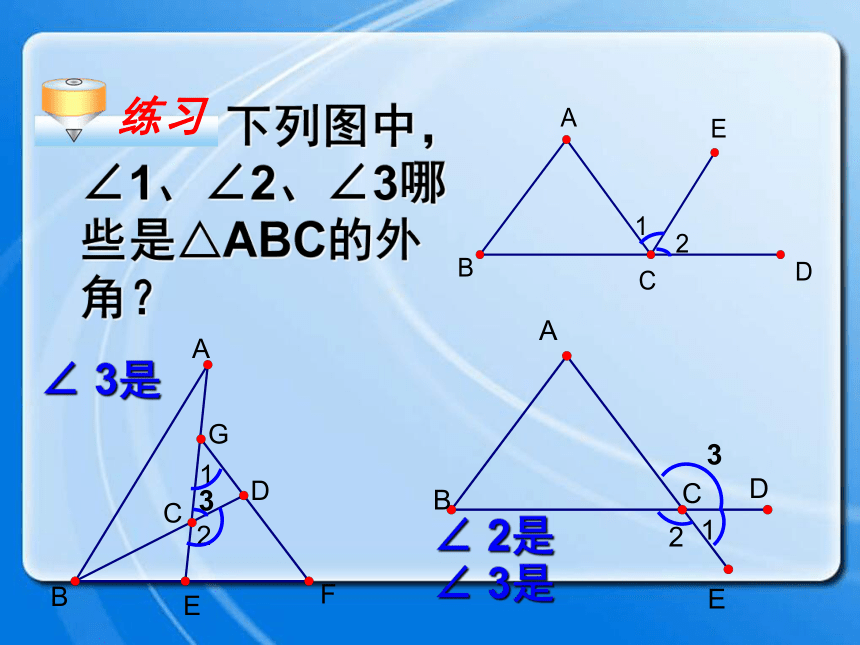
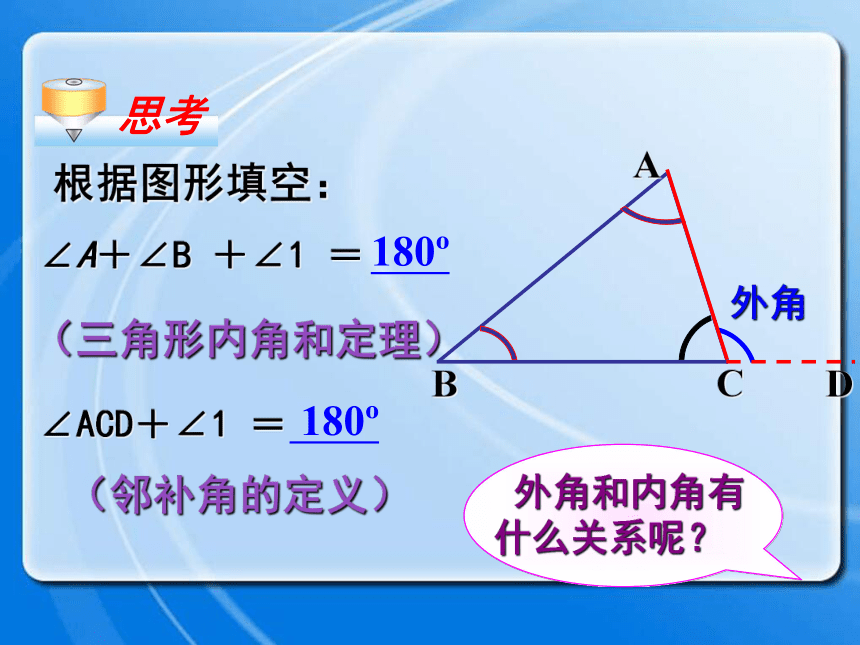
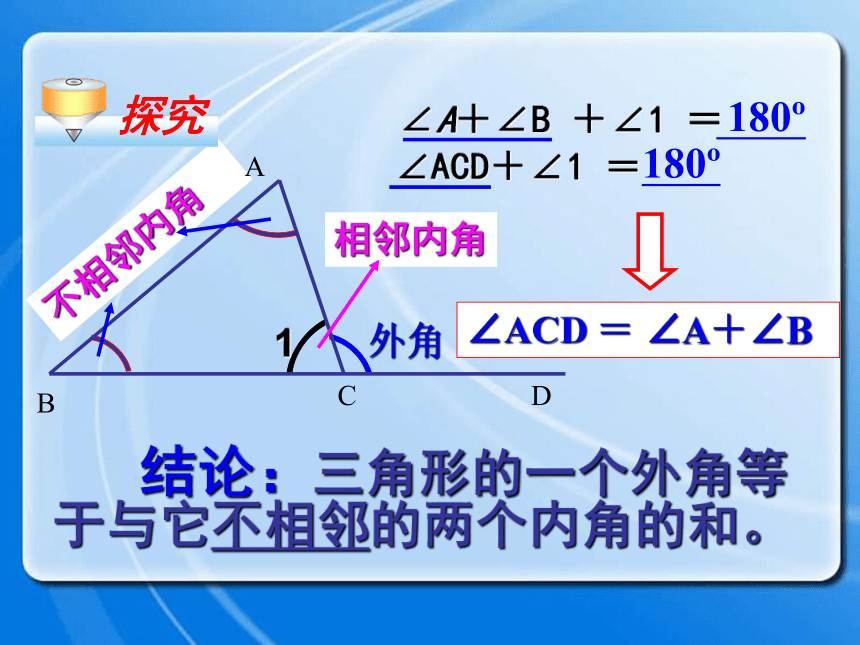
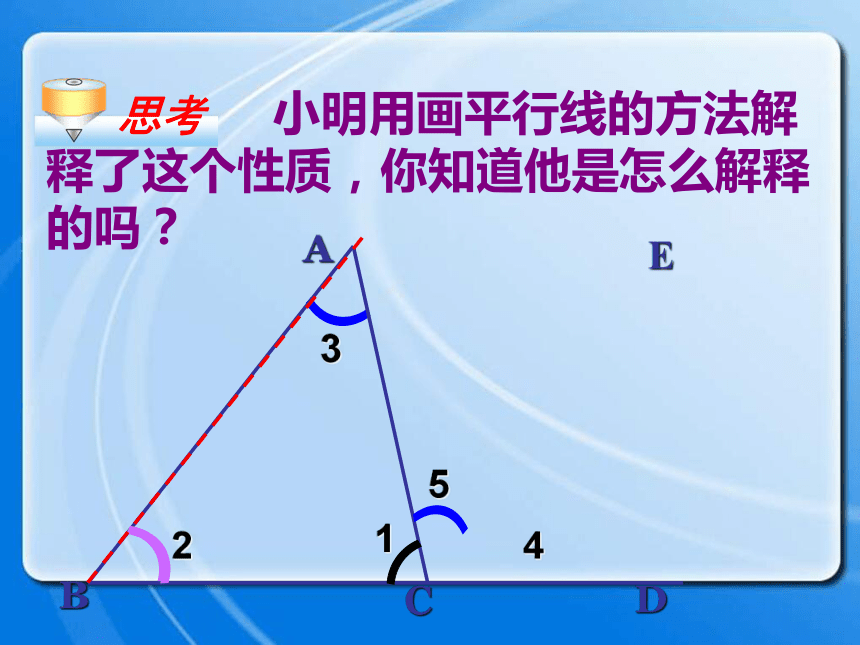
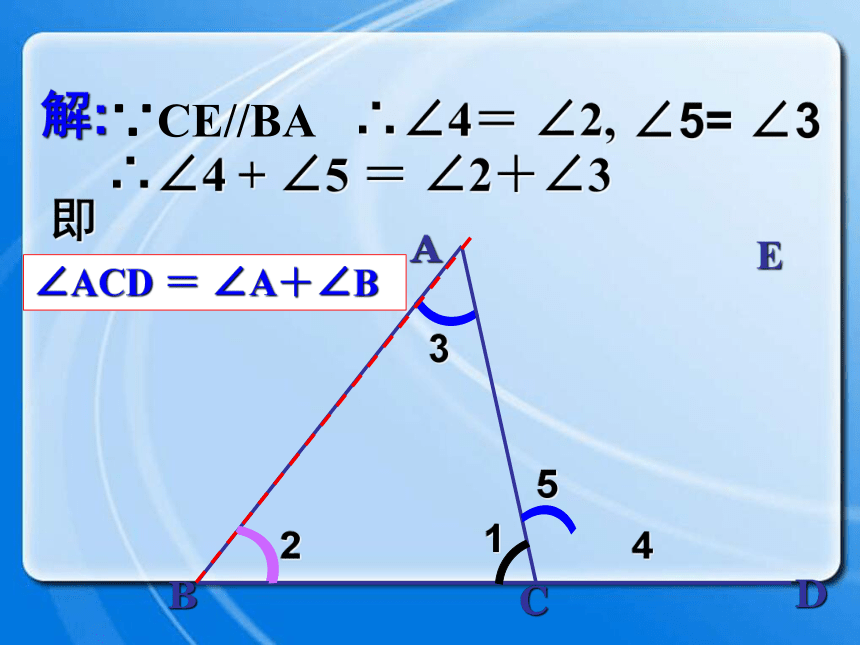
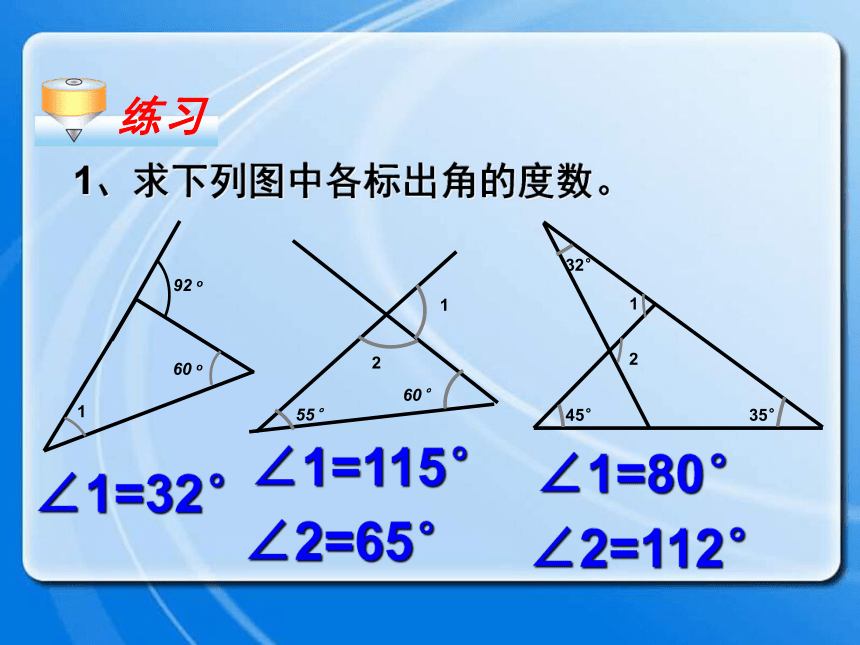
课件25张PPT。三角形的外角复习回顾1.求下列图形中∠1的度数.111155°105°28°35°30°110°60°50°90°35°75°47°B外角ACD1、什么是三角形的外角？ 三角形的一边与另一边的延长线组成的角，叫做三角形的外角.如图∠ACD.外角的定义练习 下列图中，∠1、∠2、∠3哪些是△ABC的外角？∠ 3是∠ 2是∠ 3是B外角ACD ∠A＋∠B ＋∠1 ＝ ∠ACD＋∠1 ＝180o 180o 根据图形填空：（三角形内角和定理）（邻补角的定义）思考 外角和内角有什么关系呢？外角相邻内角不相邻内角ABCD∠ACD ＝ ∠A＋∠B 结论：三角形的一个外角等于与它不相邻的两个内角的和。 ∠A＋∠B ＋∠1 ＝ ∠ACD＋∠1 ＝180o 180o 探究1 小明用画平行线的方法解释了这个性质，你知道他是怎么解释的吗？AECBD13542思考∵CE//BAAECBD13542∴∠4＝ ∠2,∠ACD ＝ ∠A＋∠B∴∠4 + ∠5 ＝ ∠2＋∠3∠5= ∠3解:即1、求下列图中各标出角的度数。练习∠1=32°∠1=115°∠2=65°∠1=80°∠2=112°B40oCDA 2、如图D是ΔABC中AC边上一点，∠C=∠DBC，∠A=∠BDA, ∠ABD＝40°，求∠C度数。∠C＝35° ∠ACD ∠A (<、=、>)；∠ACD ∠B (<、=、>) 结论：三角形的一个外角大于任何一个与它不相邻的内角。D>>探究填空： 把图中∠1、 ∠2、 ∠3按由大到小的顺序排列∠1∠2∠3＞＞练习三角形的外角与内角的关系： 1、三角形的一个外角与它相邻的内角 ；
2、三角形的一个外角 与它不相邻的两个内角的和；
3、三角形的一个外角 任何一个与它不相邻的内角。等于大于互补小结三角形的外角和360°探究 一个三角形有几个外角？它的外角和是多少？∠2＋∠ABC=180°∠3＋∠ACB=180°三个式子相加得到∠1＋∠2＋∠3＋∠BAC＋∠ABC＋∠ACB=540°又∵∠BAC＋∠ABC＋∠ACB=180°∴∠1＋∠2＋∠3＝360°∠1＋∠BAC=180°解：方法一过A作AD平行于BC∴∠3＝∠4∠2＝∠BAD∴∠1＋ ∠2＋ ∠3 ＝∠1＋∠4＋∠BAD ＝360°∴∠2＋ ∠ 3＝ ∠ 4＋∠BAD方法二解：① 、三角形的外角和是指三角形所有外角的和。
② 、三角形的外角和等于它内角和的2倍。
③ 、三角形的一个外角等于两个内角的和。
④ 、三角形的一个外角等于与它不相邻的两个内角的和。
⑤ 、三角形的一个外角大于任何一个内角。
⑥ 、三角形的一个内角小于任何一个与它不相邻的外角。巩固练习1、判断： 2、如图D是ΔABC中AC边上一点，∠C=∠DBC，若∠BDA=80°， ∠ ABC=70°，求∠A；∠C度数。∠C=40°∠A=70° 4、 ∠1， ∠2， ∠3为ΔABC的外角，若∠1：∠2：∠3＝2：3：4，则
∠ABC等于 . 3、如果三角形的一个外角与它不相邻的两个内角的和为180°，那么这个外角等于 .90°60° 用牛皮筋拉成一个五角星，看哪一个四人小组的同学速度最快。拓展探索(1)求∠A+∠B+∠C+∠D+∠E的度数180°(2)求∠A+∠B+∠C+∠D+∠E+∠F的度数360°1.若∠C=30°,求∠A+ ∠B+ ∠D+ ∠E的值.思考210° 2.你可以想出多少种方法计算：
∠A+∠B+∠C+∠D+∠E的度数。180°
谢谢！