24.2.1点和圆的位置关系 同步测试 含答案
文档属性
| 名称 | 24.2.1点和圆的位置关系 同步测试 含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 131.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-30 21:55:27 | ||
图片预览




文档简介
《24.2.1
点和圆的位置关系》
一、选择题
1.下列说法正确的是( )
A.过一点A的圆的圆心可以是平面上任意点
B.过两点A、B的圆的圆心在一条直线上
C.过三点A、B、C的圆的圆心有且只有一点
D.过四点A、B、C、D的圆不存在
2.若△ABC的外接圆的圆心在△ABC的内部,则△ABC是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
3.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,则它的外心与顶点C的距离为( )
A.5cm
B.6cm
C.7cm
D.8cm
4.如图所示,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(﹣2,4),则该圆弧所在圆的圆心坐标是( )
A.(﹣1,2)
B.(1,﹣1)
C.(﹣1,1)
D.(2,1)
5.Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙A的位置关系是( )
A.点D在⊙A外
B.点D在⊙A上
C.点D在⊙A内
D.无法确定
6.若⊙A的半径为5,圆心A的坐标是(3,4),点P的坐标是(5,8),你认为点P的位置为( )
A.在⊙A内
B.在⊙A上
C.在⊙A外
D.不能确定
7.如图,⊙O是△ABC的外接圆,若∠B=30°,AC=,则⊙O的直径为( )
A.1
B.
C.2
D.
8.用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应该假设这个三角形中( )
A.有一个内角小于60°
B.每一个内角都小于60°
C.有一个内角大于60°
D.每一个内角都大于60°
二、填空题
9.点A在以O为圆心,3cm为半径的⊙O内,则点A到圆心O的距离d的范围是______.
10.如图,在△ABC中,∠ACB=90°,AC=2cm,BC=4cm,CM为中线,以C为圆心,
cm为半径作圆,则A、B、C、M四点在圆外的有______,在圆上的有______,在圆内的有______.
11.若AB=4cm,则过点A、B且半径为3cm的圆有______个.
12.在△ABC中,BC=24cm,外心O到BC的距离为6cm,则△ABC外接圆的半径为______.
13.一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这个圆的半径是______.
14.阅读下面材料:对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖.回答下列问题:
(1)边长为1cm的正方形被一个半径为r的圆所覆盖,r的最小值是______
cm;
(2)边长为1cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是______
cm.
15.若Rt△ABC的两条直角边a,b是方程x2﹣3x+1=0的两根,则Rt△ABC的外接圆面积是______.
三、解答题
16.已知圆的半径等于5cm,根据下列点P到圆心的距离:(1)4cm;(2)5cm;(3)6cm,判定点P与圆的位置关系,并说明理由.
17.在Rt△ABC中,∠C=90°,BC=3m,AC=4m,以B为圆心,以BC为半径作⊙B,D、E是AB、AC中点,A、C、D、E分别与⊙O有怎样的位置关系?(画出图形,写过程)
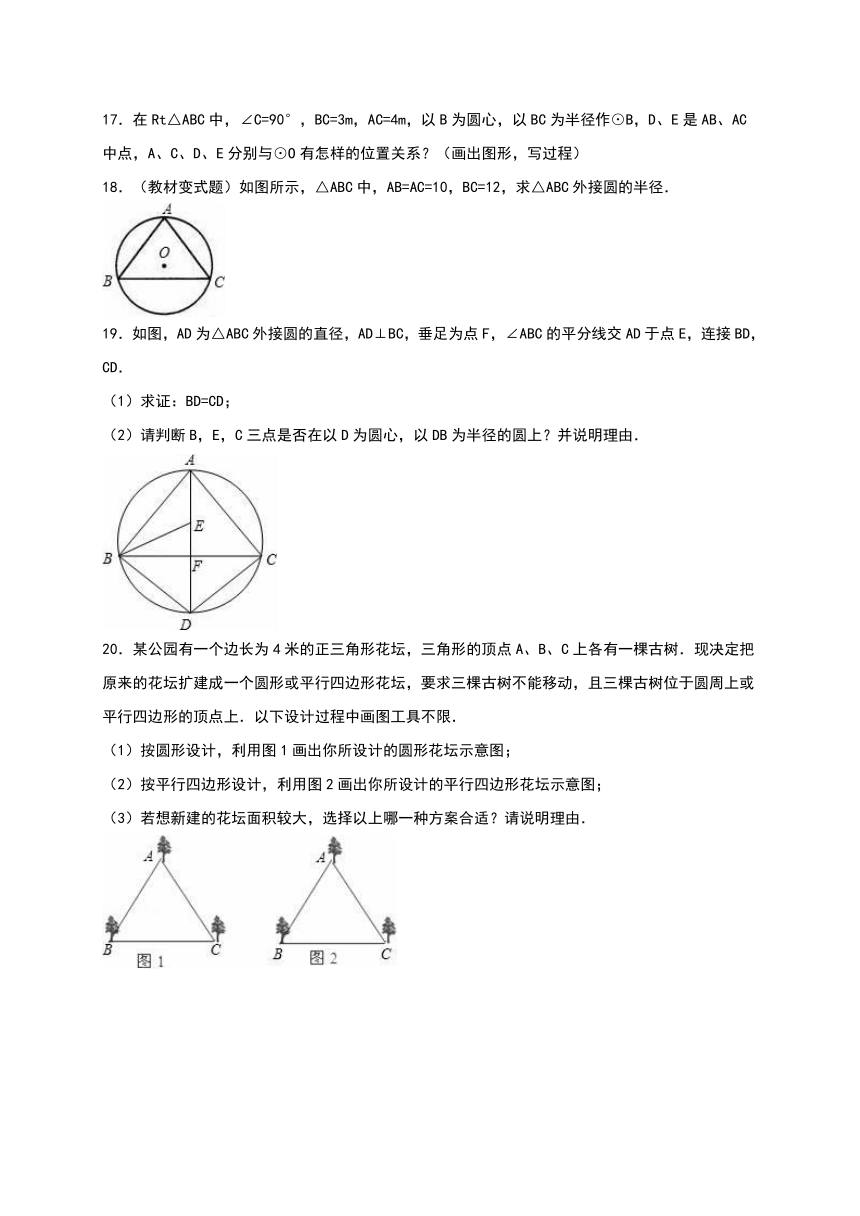
18.(教材变式题)如图所示,△ABC中,AB=AC=10,BC=12,求△ABC外接圆的半径.
19.如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
20.某公园有一个边长为4米的正三角形花坛,三角形的顶点A、B、C上各有一棵古树.现决定把原来的花坛扩建成一个圆形或平行四边形花坛,要求三棵古树不能移动,且三棵古树位于圆周上或平行四边形的顶点上.以下设计过程中画图工具不限.
(1)按圆形设计,利用图1画出你所设计的圆形花坛示意图;
(2)按平行四边形设计,利用图2画出你所设计的平行四边形花坛示意图;
(3)若想新建的花坛面积较大,选择以上哪一种方案合适?请说明理由.
《24.2.1
点和圆的位置关系》
参考答案与试题解析
一、选择题
1.下列说法正确的是( )
A.过一点A的圆的圆心可以是平面上任意点
B.过两点A、B的圆的圆心在一条直线上
C.过三点A、B、C的圆的圆心有且只有一点
D.过四点A、B、C、D的圆不存在
【解答】解:A、过一点A的圆的圆心可以是平面上任意点(A点外),故本选项错误,
B、过两点A、B的圆的圆心在一条直线上,错误,
C、正确,
D、过四点A、B、C、D的圆可以存在,故本选项错误,
故选:B.
2.若△ABC的外接圆的圆心在△ABC的内部,则△ABC是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
【解答】解:△ABC的外接圆的圆心在△ABC的内部,则△ABC是锐角三角形.
故选A.
3.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,则它的外心与顶点C的距离为( )
A.5cm
B.6cm
C.7cm
D.8cm
【解答】解:∵∠C=90°,AC=6cm,BC=8cm,
∴AB==10cm,
∵Rt△ABC的外心为斜边AB的中点,
∴Rt△ABC的外接圆半径为5cm,
∴它的外心与顶点C的距离为5cm.
故选A.
4.如图所示,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(﹣2,4),则该圆弧所在圆的圆心坐标是( )
A.(﹣1,2)
B.(1,﹣1)
C.(﹣1,1)
D.(2,1)
【解答】解:如图所示,
∵AW=1,WH=3,
∴AH==;
∵BQ=3,QH=1,
∴BH==;
∴AH=BH,
同理,AD=BD,
所以GH为线段AB的垂直平分线,
易得EF为线段AC的垂直平分线,
H为圆的两条弦的垂直平分线的交点,
则BH=AH=HC,
H为圆心.
于是则该圆弧所在圆的圆心坐标是(﹣1,1).
故选C.
5.Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙A的位置关系是( )
A.点D在⊙A外
B.点D在⊙A上
C.点D在⊙A内
D.无法确定
【解答】解:根据勾股定理求得斜边AB==2,
则AD=,
∵>2,
∴点在圆外.
故选A.
6.若⊙A的半径为5,圆心A的坐标是(3,4),点P的坐标是(5,8),你认为点P的位置为( )
A.在⊙A内
B.在⊙A上
C.在⊙A外
D.不能确定
【解答】解:∵AP==2<5,
∴点P在⊙A内,
故选A.
7.如图,⊙O是△ABC的外接圆,若∠B=30°,AC=,则⊙O的直径为( )
A.1
B.
C.2
D.
【解答】解:作直径AD,连结CD,如图,
∵AD为直径,
∴∠ACD=90°,
∵∠D=∠B=30°,
∴AD=2AC=2.
故选D.
8.用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应该假设这个三角形中( )
A.有一个内角小于60°
B.每一个内角都小于60°
C.有一个内角大于60°
D.每一个内角都大于60°
【解答】解:用反证法证明“三角形中必有一个内角小于或等于60°”时,
应先假设三角形中每一个内角都不小于或等于60°,即每一个内角都大于60°.
故选:D.
二、填空题
9.点A在以O为圆心,3cm为半径的⊙O内,则点A到圆心O的距离d的范围是 0≤d<3cm .
【解答】解:∵点A在以O为圆心,3cm为半径的⊙O内,
∴点A到圆心O的距离d的范围是:0≤d<3cm.
故答案为:0≤d<3cm.
10.如图,在△ABC中,∠ACB=90°,AC=2cm,BC=4cm,CM为中线,以C为圆心,
cm为半径作圆,则A、B、C、M四点在圆外的有 点B; ,在圆上的有 点M; ,在圆内的有 点A、C. .
【解答】解:∵△ABC中,∠ACB=90°,AC=2cm,BC=4cm,
∴AB==2,
∵CM为中线,
∴CM=AB=,
∴AC<cm,BC>cm,
∴在圆外的有点B,在圆上的有点M,在圆内的有点C和点A,
故答案为:点B;
点M;
点A、C.
11.若AB=4cm,则过点A、B且半径为3cm的圆有 两 个.
【解答】解:这样的圆能画2个.如图,作AB的垂直平分线l,再以点A为圆心,3cm为半径作圆交l于O1和O2,然后分别以O1和O2为圆心,以3cm为半径作圆,
则⊙O1和⊙O2为所求圆.
故答案为:两.
12.在△ABC中,BC=24cm,外心O到BC的距离为6cm,则△ABC外接圆的半径为 .
【解答】解:过O作OD⊥BC,由垂径定理得,
BD=BC=12cm,
在Rt△OBD中,OD=6cm,BD=12cm,
∴OB==cm,
即△ABC外接圆的半径为cm.
13.一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这个圆的半径是 6.5cm或2.5cm .
【解答】解:点P应分为位于圆的内部与外部两种情况讨论:
①当点P在圆内时,最近点的距离为4cm,最远点的距离为9cm,则直径是4+9=13cm,因而半径是6.5cm;
②当点P在圆外时,最近点的距离为4cm,最远点的距离为9cm,则直径是9﹣4=5cm,因而半径是2.5cm.
故答案为6.5cm或2.5cm.
14.阅读下面材料:对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖.回答下列问题:
(1)边长为1cm的正方形被一个半径为r的圆所覆盖,r的最小值是
cm;
(2)边长为1cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是
cm.
【解答】解:(1)正方形ABCD的边长为1cm,则正方形ABCD被一个半径为r的圆所覆盖,r的最小值为其外接圆的半径,如图1,正方形ABCD的外接圆为⊙0,
∵∠B=90°,
∴AC为直径,
∴AC=AB=,
∴OA=,
∴r的最小值是cm;
(2)边长为1cm的等边三角形ABC被一个半径为r的圆所覆盖,r的最小值为其外接圆的半径,如图2,等边三角形ABC的外接圆为⊙0,
连结OB,作OD⊥BC于D,
∵点O为等边三角形ABC的外心,
∴OB平分∠ABC,
∴∠OBD=30°,
∵OD⊥BC,
∴BD=BC=,
在Rt△BOD中,∵cos∠OBD=,
∴OB===,
∴r的最小值是cm.
故答案为;.
15.若Rt△ABC的两条直角边a,b是方程x2﹣3x+1=0的两根,则Rt△ABC的外接圆面积是 π .
【解答】解:∵圆的半径r=c,
根据两直角边a、b分别是一元二次方程x2﹣3x+1=0的两根,可得
a+b=3,a b=1,
∴c2=a2+b2=(a+b)2﹣2a b=7,
∴Rt△的外接圆的面积为πr2=π×()2=π.
故答案为:π.
三、解答题
16.已知圆的半径等于5cm,根据下列点P到圆心的距离:(1)4cm;(2)5cm;(3)6cm,判定点P与圆的位置关系,并说明理由.
【解答】解:(1)当d=4
cm时,
∵d<r,
∴点P在圆内;
(2)当d=5
cm时,
∵d=r,
∴点P在圆上;
(3)当d=6
cm时,
∵d>r,
∴点P在圆外.
17.在Rt△ABC中,∠C=90°,BC=3m,AC=4m,以B为圆心,以BC为半径作⊙B,D、E是AB、AC中点,A、C、D、E分别与⊙O有怎样的位置关系?(画出图形,写过程)
【解答】解:∵BC=3=R,
∴点C在⊙B上,
∵AB=5>3,
∴点A在⊙B外,
∵D为BA中点,
∴,
∴点D在⊙B内,
∵E为AC中点,
∴,
连结BE,
∴BE===>3m,
∴E在⊙B外.
18.(教材变式题)如图所示,△ABC中,AB=AC=10,BC=12,求△ABC外接圆的半径.
【解答】解:如图,作AD⊥BC,垂足为D,则O一定在AD上,
所以AD==8;
设OA=r,OB2=OD2+BD2,
即r2=(8﹣r)2+62,
解得r=.
答:△ABC外接圆的半径为.
19.如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
【解答】(1)证明:∵AD为直径,AD⊥BC,
∴由垂径定理得:
∴根据圆心角、弧、弦之间的关系得:BD=CD.
(2)解:B,E,C三点在以D为圆心,以DB为半径的圆上.
理由:由(1)知:,
∴∠1=∠2,
又∵∠2=∠3,
∴∠1=∠3,
∴∠DBE=∠3+∠4,∠DEB=∠1+∠5,
∵BE是∠ABC的平分线,
∴∠4=∠5,
∴∠DBE=∠DEB,
∴DB=DE.
由(1)知:BD=CD
∴DB=DE=DC.
∴B,E,C三点在以D为圆心,以DB为半径的圆上.(7分)
20.某公园有一个边长为4米的正三角形花坛,三角形的顶点A、B、C上各有一棵古树.现决定把原来的花坛扩建成一个圆形或平行四边形花坛,要求三棵古树不能移动,且三棵古树位于圆周上或平行四边形的顶点上.以下设计过程中画图工具不限.
(1)按圆形设计,利用图1画出你所设计的圆形花坛示意图;
(2)按平行四边形设计,利用图2画出你所设计的平行四边形花坛示意图;
(3)若想新建的花坛面积较大,选择以上哪一种方案合适?请说明理由.
【解答】解:
(1)(2)
;
(3)连接OB,OA,并延长AO交BC于D,
∵r=OB==,
∴S⊙O=πr2=≈16.75,
又S平行四边形=2S△ABC=2××42×sin60°=8≈13.86,
∵S⊙O>S平行四边形,
∴选择建圆形花坛面积较大.
点和圆的位置关系》
一、选择题
1.下列说法正确的是( )
A.过一点A的圆的圆心可以是平面上任意点
B.过两点A、B的圆的圆心在一条直线上
C.过三点A、B、C的圆的圆心有且只有一点
D.过四点A、B、C、D的圆不存在
2.若△ABC的外接圆的圆心在△ABC的内部,则△ABC是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
3.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,则它的外心与顶点C的距离为( )
A.5cm
B.6cm
C.7cm
D.8cm
4.如图所示,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(﹣2,4),则该圆弧所在圆的圆心坐标是( )
A.(﹣1,2)
B.(1,﹣1)
C.(﹣1,1)
D.(2,1)
5.Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙A的位置关系是( )
A.点D在⊙A外
B.点D在⊙A上
C.点D在⊙A内
D.无法确定
6.若⊙A的半径为5,圆心A的坐标是(3,4),点P的坐标是(5,8),你认为点P的位置为( )
A.在⊙A内
B.在⊙A上
C.在⊙A外
D.不能确定
7.如图,⊙O是△ABC的外接圆,若∠B=30°,AC=,则⊙O的直径为( )
A.1
B.
C.2
D.
8.用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应该假设这个三角形中( )
A.有一个内角小于60°
B.每一个内角都小于60°
C.有一个内角大于60°
D.每一个内角都大于60°
二、填空题
9.点A在以O为圆心,3cm为半径的⊙O内,则点A到圆心O的距离d的范围是______.
10.如图,在△ABC中,∠ACB=90°,AC=2cm,BC=4cm,CM为中线,以C为圆心,
cm为半径作圆,则A、B、C、M四点在圆外的有______,在圆上的有______,在圆内的有______.
11.若AB=4cm,则过点A、B且半径为3cm的圆有______个.
12.在△ABC中,BC=24cm,外心O到BC的距离为6cm,则△ABC外接圆的半径为______.
13.一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这个圆的半径是______.
14.阅读下面材料:对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖.回答下列问题:
(1)边长为1cm的正方形被一个半径为r的圆所覆盖,r的最小值是______
cm;
(2)边长为1cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是______
cm.
15.若Rt△ABC的两条直角边a,b是方程x2﹣3x+1=0的两根,则Rt△ABC的外接圆面积是______.
三、解答题
16.已知圆的半径等于5cm,根据下列点P到圆心的距离:(1)4cm;(2)5cm;(3)6cm,判定点P与圆的位置关系,并说明理由.
17.在Rt△ABC中,∠C=90°,BC=3m,AC=4m,以B为圆心,以BC为半径作⊙B,D、E是AB、AC中点,A、C、D、E分别与⊙O有怎样的位置关系?(画出图形,写过程)
18.(教材变式题)如图所示,△ABC中,AB=AC=10,BC=12,求△ABC外接圆的半径.
19.如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
20.某公园有一个边长为4米的正三角形花坛,三角形的顶点A、B、C上各有一棵古树.现决定把原来的花坛扩建成一个圆形或平行四边形花坛,要求三棵古树不能移动,且三棵古树位于圆周上或平行四边形的顶点上.以下设计过程中画图工具不限.
(1)按圆形设计,利用图1画出你所设计的圆形花坛示意图;
(2)按平行四边形设计,利用图2画出你所设计的平行四边形花坛示意图;
(3)若想新建的花坛面积较大,选择以上哪一种方案合适?请说明理由.
《24.2.1
点和圆的位置关系》
参考答案与试题解析
一、选择题
1.下列说法正确的是( )
A.过一点A的圆的圆心可以是平面上任意点
B.过两点A、B的圆的圆心在一条直线上
C.过三点A、B、C的圆的圆心有且只有一点
D.过四点A、B、C、D的圆不存在
【解答】解:A、过一点A的圆的圆心可以是平面上任意点(A点外),故本选项错误,
B、过两点A、B的圆的圆心在一条直线上,错误,
C、正确,
D、过四点A、B、C、D的圆可以存在,故本选项错误,
故选:B.
2.若△ABC的外接圆的圆心在△ABC的内部,则△ABC是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
【解答】解:△ABC的外接圆的圆心在△ABC的内部,则△ABC是锐角三角形.
故选A.
3.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,则它的外心与顶点C的距离为( )
A.5cm
B.6cm
C.7cm
D.8cm
【解答】解:∵∠C=90°,AC=6cm,BC=8cm,
∴AB==10cm,
∵Rt△ABC的外心为斜边AB的中点,
∴Rt△ABC的外接圆半径为5cm,
∴它的外心与顶点C的距离为5cm.
故选A.
4.如图所示,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(﹣2,4),则该圆弧所在圆的圆心坐标是( )
A.(﹣1,2)
B.(1,﹣1)
C.(﹣1,1)
D.(2,1)
【解答】解:如图所示,
∵AW=1,WH=3,
∴AH==;
∵BQ=3,QH=1,
∴BH==;
∴AH=BH,
同理,AD=BD,
所以GH为线段AB的垂直平分线,
易得EF为线段AC的垂直平分线,
H为圆的两条弦的垂直平分线的交点,
则BH=AH=HC,
H为圆心.
于是则该圆弧所在圆的圆心坐标是(﹣1,1).
故选C.
5.Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙A的位置关系是( )
A.点D在⊙A外
B.点D在⊙A上
C.点D在⊙A内
D.无法确定
【解答】解:根据勾股定理求得斜边AB==2,
则AD=,
∵>2,
∴点在圆外.
故选A.
6.若⊙A的半径为5,圆心A的坐标是(3,4),点P的坐标是(5,8),你认为点P的位置为( )
A.在⊙A内
B.在⊙A上
C.在⊙A外
D.不能确定
【解答】解:∵AP==2<5,
∴点P在⊙A内,
故选A.
7.如图,⊙O是△ABC的外接圆,若∠B=30°,AC=,则⊙O的直径为( )
A.1
B.
C.2
D.
【解答】解:作直径AD,连结CD,如图,
∵AD为直径,
∴∠ACD=90°,
∵∠D=∠B=30°,
∴AD=2AC=2.
故选D.
8.用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应该假设这个三角形中( )
A.有一个内角小于60°
B.每一个内角都小于60°
C.有一个内角大于60°
D.每一个内角都大于60°
【解答】解:用反证法证明“三角形中必有一个内角小于或等于60°”时,
应先假设三角形中每一个内角都不小于或等于60°,即每一个内角都大于60°.
故选:D.
二、填空题
9.点A在以O为圆心,3cm为半径的⊙O内,则点A到圆心O的距离d的范围是 0≤d<3cm .
【解答】解:∵点A在以O为圆心,3cm为半径的⊙O内,
∴点A到圆心O的距离d的范围是:0≤d<3cm.
故答案为:0≤d<3cm.
10.如图,在△ABC中,∠ACB=90°,AC=2cm,BC=4cm,CM为中线,以C为圆心,
cm为半径作圆,则A、B、C、M四点在圆外的有 点B; ,在圆上的有 点M; ,在圆内的有 点A、C. .
【解答】解:∵△ABC中,∠ACB=90°,AC=2cm,BC=4cm,
∴AB==2,
∵CM为中线,
∴CM=AB=,
∴AC<cm,BC>cm,
∴在圆外的有点B,在圆上的有点M,在圆内的有点C和点A,
故答案为:点B;
点M;
点A、C.
11.若AB=4cm,则过点A、B且半径为3cm的圆有 两 个.
【解答】解:这样的圆能画2个.如图,作AB的垂直平分线l,再以点A为圆心,3cm为半径作圆交l于O1和O2,然后分别以O1和O2为圆心,以3cm为半径作圆,
则⊙O1和⊙O2为所求圆.
故答案为:两.
12.在△ABC中,BC=24cm,外心O到BC的距离为6cm,则△ABC外接圆的半径为 .
【解答】解:过O作OD⊥BC,由垂径定理得,
BD=BC=12cm,
在Rt△OBD中,OD=6cm,BD=12cm,
∴OB==cm,
即△ABC外接圆的半径为cm.
13.一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这个圆的半径是 6.5cm或2.5cm .
【解答】解:点P应分为位于圆的内部与外部两种情况讨论:
①当点P在圆内时,最近点的距离为4cm,最远点的距离为9cm,则直径是4+9=13cm,因而半径是6.5cm;
②当点P在圆外时,最近点的距离为4cm,最远点的距离为9cm,则直径是9﹣4=5cm,因而半径是2.5cm.
故答案为6.5cm或2.5cm.
14.阅读下面材料:对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖.回答下列问题:
(1)边长为1cm的正方形被一个半径为r的圆所覆盖,r的最小值是
cm;
(2)边长为1cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是
cm.
【解答】解:(1)正方形ABCD的边长为1cm,则正方形ABCD被一个半径为r的圆所覆盖,r的最小值为其外接圆的半径,如图1,正方形ABCD的外接圆为⊙0,
∵∠B=90°,
∴AC为直径,
∴AC=AB=,
∴OA=,
∴r的最小值是cm;
(2)边长为1cm的等边三角形ABC被一个半径为r的圆所覆盖,r的最小值为其外接圆的半径,如图2,等边三角形ABC的外接圆为⊙0,
连结OB,作OD⊥BC于D,
∵点O为等边三角形ABC的外心,
∴OB平分∠ABC,
∴∠OBD=30°,
∵OD⊥BC,
∴BD=BC=,
在Rt△BOD中,∵cos∠OBD=,
∴OB===,
∴r的最小值是cm.
故答案为;.
15.若Rt△ABC的两条直角边a,b是方程x2﹣3x+1=0的两根,则Rt△ABC的外接圆面积是 π .
【解答】解:∵圆的半径r=c,
根据两直角边a、b分别是一元二次方程x2﹣3x+1=0的两根,可得
a+b=3,a b=1,
∴c2=a2+b2=(a+b)2﹣2a b=7,
∴Rt△的外接圆的面积为πr2=π×()2=π.
故答案为:π.
三、解答题
16.已知圆的半径等于5cm,根据下列点P到圆心的距离:(1)4cm;(2)5cm;(3)6cm,判定点P与圆的位置关系,并说明理由.
【解答】解:(1)当d=4
cm时,
∵d<r,
∴点P在圆内;
(2)当d=5
cm时,
∵d=r,
∴点P在圆上;
(3)当d=6
cm时,
∵d>r,
∴点P在圆外.
17.在Rt△ABC中,∠C=90°,BC=3m,AC=4m,以B为圆心,以BC为半径作⊙B,D、E是AB、AC中点,A、C、D、E分别与⊙O有怎样的位置关系?(画出图形,写过程)
【解答】解:∵BC=3=R,
∴点C在⊙B上,
∵AB=5>3,
∴点A在⊙B外,
∵D为BA中点,
∴,
∴点D在⊙B内,
∵E为AC中点,
∴,
连结BE,
∴BE===>3m,
∴E在⊙B外.
18.(教材变式题)如图所示,△ABC中,AB=AC=10,BC=12,求△ABC外接圆的半径.
【解答】解:如图,作AD⊥BC,垂足为D,则O一定在AD上,
所以AD==8;
设OA=r,OB2=OD2+BD2,
即r2=(8﹣r)2+62,
解得r=.
答:△ABC外接圆的半径为.
19.如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
【解答】(1)证明:∵AD为直径,AD⊥BC,
∴由垂径定理得:
∴根据圆心角、弧、弦之间的关系得:BD=CD.
(2)解:B,E,C三点在以D为圆心,以DB为半径的圆上.
理由:由(1)知:,
∴∠1=∠2,
又∵∠2=∠3,
∴∠1=∠3,
∴∠DBE=∠3+∠4,∠DEB=∠1+∠5,
∵BE是∠ABC的平分线,
∴∠4=∠5,
∴∠DBE=∠DEB,
∴DB=DE.
由(1)知:BD=CD
∴DB=DE=DC.
∴B,E,C三点在以D为圆心,以DB为半径的圆上.(7分)
20.某公园有一个边长为4米的正三角形花坛,三角形的顶点A、B、C上各有一棵古树.现决定把原来的花坛扩建成一个圆形或平行四边形花坛,要求三棵古树不能移动,且三棵古树位于圆周上或平行四边形的顶点上.以下设计过程中画图工具不限.
(1)按圆形设计,利用图1画出你所设计的圆形花坛示意图;
(2)按平行四边形设计,利用图2画出你所设计的平行四边形花坛示意图;
(3)若想新建的花坛面积较大,选择以上哪一种方案合适?请说明理由.
【解答】解:
(1)(2)
;
(3)连接OB,OA,并延长AO交BC于D,
∵r=OB==,
∴S⊙O=πr2=≈16.75,
又S平行四边形=2S△ABC=2××42×sin60°=8≈13.86,
∵S⊙O>S平行四边形,
∴选择建圆形花坛面积较大.
同课章节目录
