九年级上数学24.1.4圆同步测试(含答案)
文档属性
| 名称 | 九年级上数学24.1.4圆同步测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 190.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-01 06:45:21 | ||
图片预览



文档简介
《24.1.4
圆》
一、选择题
1.如图,在⊙O中,若C是的中点,则图中与∠BAC相等的角有( )
A.1个
B.2个
C.3个
D.4个
2.如图,△ABC内接于⊙O,∠A=40°,则∠BOC的度数为( )
A.20°
B.40°
C.60°
D.80°
3.如图,AB是⊙O的直径,点C在⊙O上,若∠A=40°,则∠B的度数为( )
A.80°
B.60°
C.50°
D.40°
4.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为( )
A.50°
B.60°
C.70°
D.80°
5.如图,AB、CD是⊙O的两条弦,连接AD、BC.若∠BAD=60°,则∠BCD的度数为( )
A.40°
B.50°
C.60°
D.70°
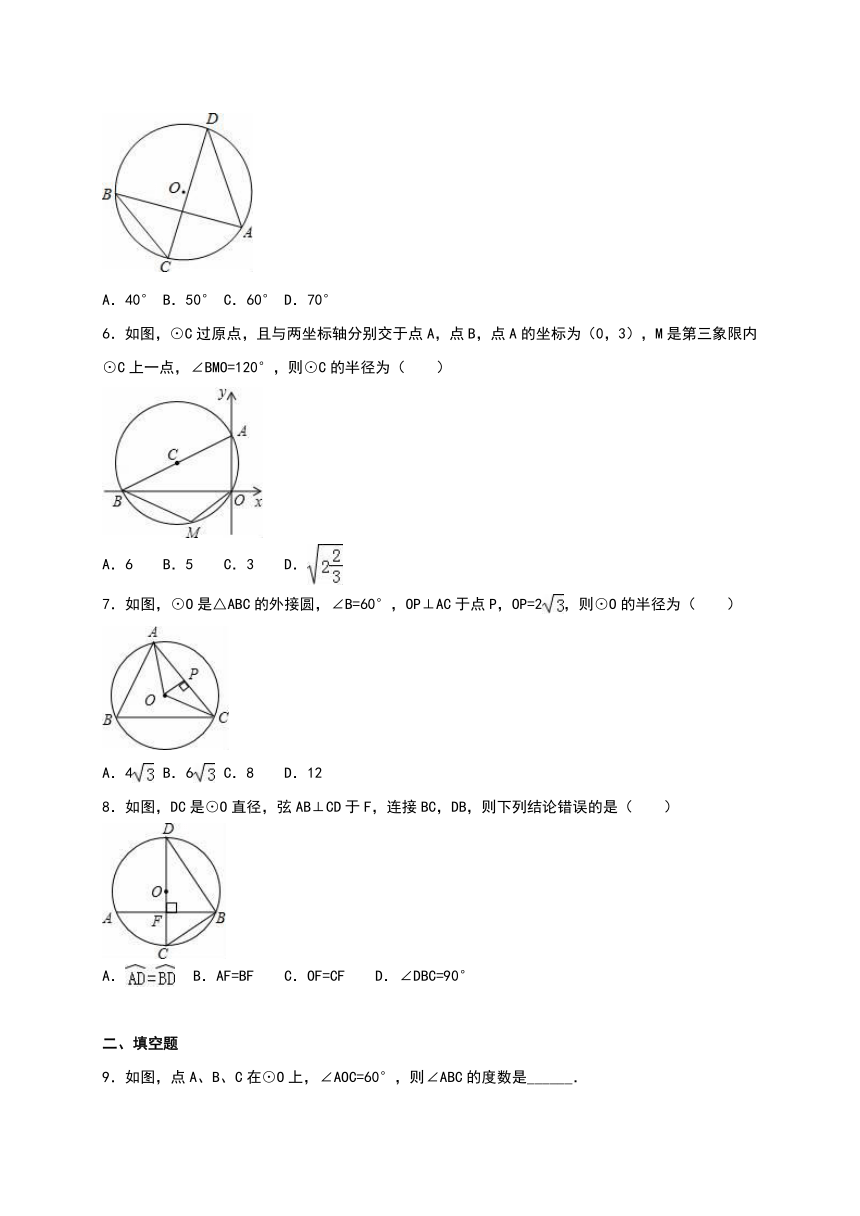
6.如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内⊙C上一点,∠BMO=120°,则⊙C的半径为( )
A.6
B.5
C.3
D.
7.如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,OP=2,则⊙O的半径为( )
A.4
B.6
C.8
D.12
8.如图,DC是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是( )
A.
B.AF=BF
C.OF=CF
D.∠DBC=90°
二、填空题
9.如图,点A、B、C在⊙O上,∠AOC=60°,则∠ABC的度数是______.
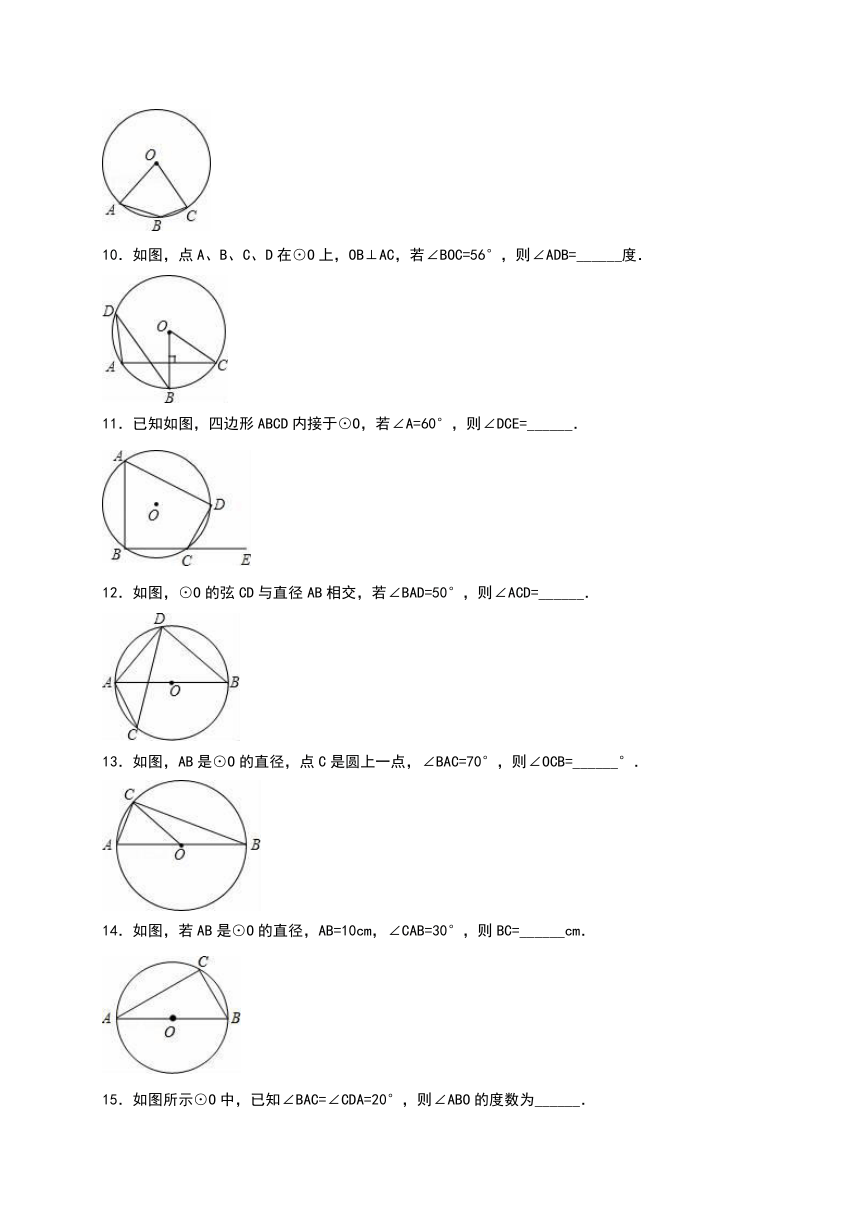
10.如图,点A、B、C、D在⊙O上,OB⊥AC,若∠BOC=56°,则∠ADB=______度.
11.已知如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE=______.
12.如图,⊙O的弦CD与直径AB相交,若∠BAD=50°,则∠ACD=______.
13.如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB=______°.
14.如图,若AB是⊙O的直径,AB=10cm,∠CAB=30°,则BC=______cm.
15.如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为______.
16.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC=______.
17.图中圆心角∠AOB=30°,弦CA∥OB,延长CO与圆交于点D,则∠BOD=______.
18.如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒,点E在量角器上对应的读数是______度.
三、解答题
19.如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
20.如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于点F.
(1)求证:CF﹦BF;
(2)若CD﹦6,AC﹦8,则⊙O的半径为______,CE的长是______.
21.如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
22.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
23.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
《24.1.4
圆》
参考答案与试题解析
一、选择题
1.如图,在⊙O中,若C是的中点,则图中与∠BAC相等的角有( )
A.1个
B.2个
C.3个
D.4个
【解答】解:∵点C是弧BD的中点,
∴,
∴∠BAC=∠CAD,
∠BAC=∠BDC,
∠CAD=∠CBD,
∴∠CAD=∠BDC=∠CBD=∠BAC,
于是图中与∠BAC相等的角共有3个,
故选C.
2.如图,△ABC内接于⊙O,∠A=40°,则∠BOC的度数为( )
A.20°
B.40°
C.60°
D.80°
【解答】解:∵∠BOC、∠A是同弧所对的圆心角和圆周角,
∴∠BOC=2∠A=80°;
故选D.
3.如图,AB是⊙O的直径,点C在⊙O上,若∠A=40°,则∠B的度数为( )
A.80°
B.60°
C.50°
D.40°
【解答】解:∵AB是⊙O的直径,
∴∠C=90°,
∵∠A=40°,
∴∠B=90°﹣∠A=50°.
故选C.
4.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为( )
A.50°
B.60°
C.70°
D.80°
【解答】解:∵∠BOD=100°,
∴∠A=∠BOD=50°,
∵∠B=60°,
∴∠C=180°﹣∠A﹣∠B=70°.
故选C.
5.如图,AB、CD是⊙O的两条弦,连接AD、BC.若∠BAD=60°,则∠BCD的度数为( )
A.40°
B.50°
C.60°
D.70°
【解答】解:∵∠BAD与∠BCD都是对的圆周角,
∴∠BCD=∠BAD=60°.
故选C.
6.如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内⊙C上一点,∠BMO=120°,则⊙C的半径为( )
A.6
B.5
C.3
D.
【解答】解:∵∠AOB=90°,
∴AB是直径,
∴∠BAM+∠OAM=∠BOM+∠OBM=180°﹣120°=60°,
∴∠BAO=60°,
∵点A的坐标为(0,3),
∴AO=3,
∴cos∠BAO=,
∴AB==6,
∴⊙C的半径为3,
故选C.
7.如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,OP=2,则⊙O的半径为( )
A.4
B.6
C.8
D.12
【解答】解:∵圆心角∠AOC与圆周角∠B所对的弧都为,且∠B=60°,
∴∠AOC=2∠B=120°,
又OA=OC,
∴∠OAC=∠OCA=30°,
∵OP⊥AC,
∴∠APO=90°,
在Rt△AOP中,OP=2,∠OAC=30°,
∴OA=2OP=4,
则圆O的半径4.
故选A
8.如图,DC是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是( )
A.
B.AF=BF
C.OF=CF
D.∠DBC=90°
【解答】解:∵DC是⊙O直径,弦AB⊥CD于F,
∴点D是优弧AB的中点,点C是劣弧AB的中点,
A、=,正确,故本选项错误;
B、AF=BF,正确,故本选项错误;
C、OF=CF,不能得出,错误,故本选项符合题意;
D、∠DBC=90°,正确,故本选项错误;
故选C.
二、填空题
9.如图,点A、B、C在⊙O上,∠AOC=60°,则∠ABC的度数是 150° .
【解答】解:在优弧上取点D,连接AD,CD,
∵∠AOC=60°,
∴∠ADC=∠AOC=30°,
∵∠ABC+∠ADC=180°,
∴∠ABC=180°﹣∠ADC=180°﹣30°=150°.
故答案为:150°.
10.如图,点A、B、C、D在⊙O上,OB⊥AC,若∠BOC=56°,则∠ADB= 28 度.
【解答】解:∵OB⊥AC,
∴=,
∴∠ADB=∠BOC=28°.
故答案为:28.
11.已知如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE= 60° .
【解答】解:∵四边形ABCD是圆内接四边形,
∴∠A+∠BCD=180°,
∵∠BCD+∠DCE=180°,
∴∠DCE=∠A.
∵∠A=60°,
∴∠DCE=60°.
故答案为:60°.
12.如图,⊙O的弦CD与直径AB相交,若∠BAD=50°,则∠ACD= 40° .
【解答】解:∵AB为圆的直径,
∴∠ADB=90°,
∵∠BAD=50°,
∴∠DBA=40°,
∴∠ACD=40°.
故答案为:40°.
13.如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB= 20 °.
【解答】解:∵⊙O是△ABC的外接圆,∠BAC=70°,
∴∠B0C=2∠BAC=2×70°=140°,
∵OC=OB(都是半径),
∴∠OCB=∠OBC=(180°﹣∠BOC)=20°.
故答案为:20°.
14.如图,若AB是⊙O的直径,AB=10cm,∠CAB=30°,则BC= 5 cm.
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵AB=10cm,∠CAB=30°,
∴BC=AB=5cm.
故答案为:5.
15.如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为 50° .
【解答】解:连接OA,
由题意得,∠AOB=2(∠ADC+∠BAC)=80°,
∵OA=OB(都是半径),
∴∠ABO=∠OAB=(180°﹣∠AOB)=50°.
故答案为:50°.
16.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= 2 .
【解答】解:∵BD为⊙O的直径,
∴∠BAD=∠BCD=90°,
∵∠BAC=120°,
∴∠CAD=120°﹣90°=30°,
∴∠CBD=∠CAD=30°,
又∵∠BAC=120°,
∴∠BDC=180°﹣∠BAC=180°﹣120°=60°,
∵AB=AC,
∴∠ADB=∠ADC,
∴∠ADB=∠BDC=×60°=30°,
∵AD=6,
∴在Rt△ABD中,BD=AD÷sin60°=6÷=4,
在Rt△BCD中,DC=BD=×4=2.
故答案为:2.
17.图中圆心角∠AOB=30°,弦CA∥OB,延长CO与圆交于点D,则∠BOD= 30° .
【解答】解:∵CA∥OB,
∴∠CAO=∠AOB=30°,
∵OA=OC,
∴∠C=∠OAC=30°,
∴∠AOD=2∠C=60°,
∴∠BOD=60°﹣30°=30°.
故答案为30°.
18.如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒,点E在量角器上对应的读数是 144 度.
【解答】解:连接OE,
∵∠ACB=90°,
∴A,B,C在以点O为圆心,AB为直径的圆上,
∴点E,A,B,C共圆,
∵∠ACE=3×24=72°,
∴∠AOE=2∠ACE=144°.
∴点E在量角器上对应的读数是:144°.
故答案为:144.
三、解答题
19.如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
【解答】解:∵AB是直径
∴∠ACB=∠ADB=90°
在Rt△ABC中,AB2=AC2+BC2,AB=10cm,AC=6cm
∴BC2=AB2﹣AC2=102﹣62=64
∴BC==8(cm)
又CD平分∠ACB,
∴∠ACD=∠BCD,
∴
∴AD=BD
又在Rt△ABD中,AD2+BD2=AB2
∴AD2+BD2=102
∴AD=BD==5(cm).
20.如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于点F.
(1)求证:CF﹦BF;
(2)若CD﹦6,AC﹦8,则⊙O的半径为 5 ,CE的长是 .
【解答】(1)证明:
∵AB是⊙O的直径,
∴∠ACB﹦90°
又∵CE⊥AB,
∴∠CEB﹦90°
∴∠2﹦90°﹣∠ACE﹦∠A,
∵C是的中点,
∴=,
∴∠1﹦∠A(等弧所对的圆周角相等),
∴∠1﹦∠2,
∴CF﹦BF;
(2)解:∵C是的中点,CD﹦6,
∴BC=6,
∵∠ACB﹦90°,
∴AB2=AC2+BC2,
又∵BC=CD,
∴AB2=64+36=100,
∴AB=10,
∴CE===,
故⊙O的半径为5,CE的长是.
21.如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
【解答】(1)证明:在△ABC中,
∵∠BAC=∠APC=60°,
又∵∠APC=∠ABC,
∴∠ABC=60°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°,
∴△ABC是等边三角形;
(2)解:连接OB,
∵△ABC为等边三角形,⊙O为其外接圆,
∴O为△ABC的外心,
∴BO平分∠ABC,
∴∠OBD=30°,
∴OD=8×=4.
22.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
【解答】证明:(1)∵OD⊥AC
OD为半径,
∴=,
∴∠CBD=∠ABD,
∴BD平分∠ABC;
(2)∵OB=OD,
∴∠OBD=∠0DB=30°,
∴∠AOD=∠OBD+∠ODB=30°+30°=60°,
又∵OD⊥AC于E,
∴∠OEA=90°,
∴∠A=180°﹣∠OEA﹣∠AOD=180°﹣90°﹣60°=30°,
又∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△ACB中,BC=AB,
∵OD=AB,
∴BC=OD.
23.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
【解答】(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC⊥BC,
又∵DC=CB,
∴AD=AB,
∴∠B=∠D;
(2)解:设BC=x,则AC=x﹣2,
在Rt△ABC中,AC2+BC2=AB2,
∴(x﹣2)2+x2=42,
解得:x1=1+,x2=1﹣(舍去),
∵∠B=∠E,∠B=∠D,
∴∠D=∠E,
∴CD=CE,
∵CD=CB,
∴CE=CB=1+.
圆》
一、选择题
1.如图,在⊙O中,若C是的中点,则图中与∠BAC相等的角有( )
A.1个
B.2个
C.3个
D.4个
2.如图,△ABC内接于⊙O,∠A=40°,则∠BOC的度数为( )
A.20°
B.40°
C.60°
D.80°
3.如图,AB是⊙O的直径,点C在⊙O上,若∠A=40°,则∠B的度数为( )
A.80°
B.60°
C.50°
D.40°
4.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为( )
A.50°
B.60°
C.70°
D.80°
5.如图,AB、CD是⊙O的两条弦,连接AD、BC.若∠BAD=60°,则∠BCD的度数为( )
A.40°
B.50°
C.60°
D.70°
6.如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内⊙C上一点,∠BMO=120°,则⊙C的半径为( )
A.6
B.5
C.3
D.
7.如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,OP=2,则⊙O的半径为( )
A.4
B.6
C.8
D.12
8.如图,DC是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是( )
A.
B.AF=BF
C.OF=CF
D.∠DBC=90°
二、填空题
9.如图,点A、B、C在⊙O上,∠AOC=60°,则∠ABC的度数是______.
10.如图,点A、B、C、D在⊙O上,OB⊥AC,若∠BOC=56°,则∠ADB=______度.
11.已知如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE=______.
12.如图,⊙O的弦CD与直径AB相交,若∠BAD=50°,则∠ACD=______.
13.如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB=______°.
14.如图,若AB是⊙O的直径,AB=10cm,∠CAB=30°,则BC=______cm.
15.如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为______.
16.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC=______.
17.图中圆心角∠AOB=30°,弦CA∥OB,延长CO与圆交于点D,则∠BOD=______.
18.如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒,点E在量角器上对应的读数是______度.
三、解答题
19.如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
20.如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于点F.
(1)求证:CF﹦BF;
(2)若CD﹦6,AC﹦8,则⊙O的半径为______,CE的长是______.
21.如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
22.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
23.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
《24.1.4
圆》
参考答案与试题解析
一、选择题
1.如图,在⊙O中,若C是的中点,则图中与∠BAC相等的角有( )
A.1个
B.2个
C.3个
D.4个
【解答】解:∵点C是弧BD的中点,
∴,
∴∠BAC=∠CAD,
∠BAC=∠BDC,
∠CAD=∠CBD,
∴∠CAD=∠BDC=∠CBD=∠BAC,
于是图中与∠BAC相等的角共有3个,
故选C.
2.如图,△ABC内接于⊙O,∠A=40°,则∠BOC的度数为( )
A.20°
B.40°
C.60°
D.80°
【解答】解:∵∠BOC、∠A是同弧所对的圆心角和圆周角,
∴∠BOC=2∠A=80°;
故选D.
3.如图,AB是⊙O的直径,点C在⊙O上,若∠A=40°,则∠B的度数为( )
A.80°
B.60°
C.50°
D.40°
【解答】解:∵AB是⊙O的直径,
∴∠C=90°,
∵∠A=40°,
∴∠B=90°﹣∠A=50°.
故选C.
4.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为( )
A.50°
B.60°
C.70°
D.80°
【解答】解:∵∠BOD=100°,
∴∠A=∠BOD=50°,
∵∠B=60°,
∴∠C=180°﹣∠A﹣∠B=70°.
故选C.
5.如图,AB、CD是⊙O的两条弦,连接AD、BC.若∠BAD=60°,则∠BCD的度数为( )
A.40°
B.50°
C.60°
D.70°
【解答】解:∵∠BAD与∠BCD都是对的圆周角,
∴∠BCD=∠BAD=60°.
故选C.
6.如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内⊙C上一点,∠BMO=120°,则⊙C的半径为( )
A.6
B.5
C.3
D.
【解答】解:∵∠AOB=90°,
∴AB是直径,
∴∠BAM+∠OAM=∠BOM+∠OBM=180°﹣120°=60°,
∴∠BAO=60°,
∵点A的坐标为(0,3),
∴AO=3,
∴cos∠BAO=,
∴AB==6,
∴⊙C的半径为3,
故选C.
7.如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,OP=2,则⊙O的半径为( )
A.4
B.6
C.8
D.12
【解答】解:∵圆心角∠AOC与圆周角∠B所对的弧都为,且∠B=60°,
∴∠AOC=2∠B=120°,
又OA=OC,
∴∠OAC=∠OCA=30°,
∵OP⊥AC,
∴∠APO=90°,
在Rt△AOP中,OP=2,∠OAC=30°,
∴OA=2OP=4,
则圆O的半径4.
故选A
8.如图,DC是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是( )
A.
B.AF=BF
C.OF=CF
D.∠DBC=90°
【解答】解:∵DC是⊙O直径,弦AB⊥CD于F,
∴点D是优弧AB的中点,点C是劣弧AB的中点,
A、=,正确,故本选项错误;
B、AF=BF,正确,故本选项错误;
C、OF=CF,不能得出,错误,故本选项符合题意;
D、∠DBC=90°,正确,故本选项错误;
故选C.
二、填空题
9.如图,点A、B、C在⊙O上,∠AOC=60°,则∠ABC的度数是 150° .
【解答】解:在优弧上取点D,连接AD,CD,
∵∠AOC=60°,
∴∠ADC=∠AOC=30°,
∵∠ABC+∠ADC=180°,
∴∠ABC=180°﹣∠ADC=180°﹣30°=150°.
故答案为:150°.
10.如图,点A、B、C、D在⊙O上,OB⊥AC,若∠BOC=56°,则∠ADB= 28 度.
【解答】解:∵OB⊥AC,
∴=,
∴∠ADB=∠BOC=28°.
故答案为:28.
11.已知如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE= 60° .
【解答】解:∵四边形ABCD是圆内接四边形,
∴∠A+∠BCD=180°,
∵∠BCD+∠DCE=180°,
∴∠DCE=∠A.
∵∠A=60°,
∴∠DCE=60°.
故答案为:60°.
12.如图,⊙O的弦CD与直径AB相交,若∠BAD=50°,则∠ACD= 40° .
【解答】解:∵AB为圆的直径,
∴∠ADB=90°,
∵∠BAD=50°,
∴∠DBA=40°,
∴∠ACD=40°.
故答案为:40°.
13.如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB= 20 °.
【解答】解:∵⊙O是△ABC的外接圆,∠BAC=70°,
∴∠B0C=2∠BAC=2×70°=140°,
∵OC=OB(都是半径),
∴∠OCB=∠OBC=(180°﹣∠BOC)=20°.
故答案为:20°.
14.如图,若AB是⊙O的直径,AB=10cm,∠CAB=30°,则BC= 5 cm.
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵AB=10cm,∠CAB=30°,
∴BC=AB=5cm.
故答案为:5.
15.如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为 50° .
【解答】解:连接OA,
由题意得,∠AOB=2(∠ADC+∠BAC)=80°,
∵OA=OB(都是半径),
∴∠ABO=∠OAB=(180°﹣∠AOB)=50°.
故答案为:50°.
16.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= 2 .
【解答】解:∵BD为⊙O的直径,
∴∠BAD=∠BCD=90°,
∵∠BAC=120°,
∴∠CAD=120°﹣90°=30°,
∴∠CBD=∠CAD=30°,
又∵∠BAC=120°,
∴∠BDC=180°﹣∠BAC=180°﹣120°=60°,
∵AB=AC,
∴∠ADB=∠ADC,
∴∠ADB=∠BDC=×60°=30°,
∵AD=6,
∴在Rt△ABD中,BD=AD÷sin60°=6÷=4,
在Rt△BCD中,DC=BD=×4=2.
故答案为:2.
17.图中圆心角∠AOB=30°,弦CA∥OB,延长CO与圆交于点D,则∠BOD= 30° .
【解答】解:∵CA∥OB,
∴∠CAO=∠AOB=30°,
∵OA=OC,
∴∠C=∠OAC=30°,
∴∠AOD=2∠C=60°,
∴∠BOD=60°﹣30°=30°.
故答案为30°.
18.如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒,点E在量角器上对应的读数是 144 度.
【解答】解:连接OE,
∵∠ACB=90°,
∴A,B,C在以点O为圆心,AB为直径的圆上,
∴点E,A,B,C共圆,
∵∠ACE=3×24=72°,
∴∠AOE=2∠ACE=144°.
∴点E在量角器上对应的读数是:144°.
故答案为:144.
三、解答题
19.如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
【解答】解:∵AB是直径
∴∠ACB=∠ADB=90°
在Rt△ABC中,AB2=AC2+BC2,AB=10cm,AC=6cm
∴BC2=AB2﹣AC2=102﹣62=64
∴BC==8(cm)
又CD平分∠ACB,
∴∠ACD=∠BCD,
∴
∴AD=BD
又在Rt△ABD中,AD2+BD2=AB2
∴AD2+BD2=102
∴AD=BD==5(cm).
20.如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于点F.
(1)求证:CF﹦BF;
(2)若CD﹦6,AC﹦8,则⊙O的半径为 5 ,CE的长是 .
【解答】(1)证明:
∵AB是⊙O的直径,
∴∠ACB﹦90°
又∵CE⊥AB,
∴∠CEB﹦90°
∴∠2﹦90°﹣∠ACE﹦∠A,
∵C是的中点,
∴=,
∴∠1﹦∠A(等弧所对的圆周角相等),
∴∠1﹦∠2,
∴CF﹦BF;
(2)解:∵C是的中点,CD﹦6,
∴BC=6,
∵∠ACB﹦90°,
∴AB2=AC2+BC2,
又∵BC=CD,
∴AB2=64+36=100,
∴AB=10,
∴CE===,
故⊙O的半径为5,CE的长是.
21.如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
【解答】(1)证明:在△ABC中,
∵∠BAC=∠APC=60°,
又∵∠APC=∠ABC,
∴∠ABC=60°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°,
∴△ABC是等边三角形;
(2)解:连接OB,
∵△ABC为等边三角形,⊙O为其外接圆,
∴O为△ABC的外心,
∴BO平分∠ABC,
∴∠OBD=30°,
∴OD=8×=4.
22.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
【解答】证明:(1)∵OD⊥AC
OD为半径,
∴=,
∴∠CBD=∠ABD,
∴BD平分∠ABC;
(2)∵OB=OD,
∴∠OBD=∠0DB=30°,
∴∠AOD=∠OBD+∠ODB=30°+30°=60°,
又∵OD⊥AC于E,
∴∠OEA=90°,
∴∠A=180°﹣∠OEA﹣∠AOD=180°﹣90°﹣60°=30°,
又∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△ACB中,BC=AB,
∵OD=AB,
∴BC=OD.
23.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
【解答】(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC⊥BC,
又∵DC=CB,
∴AD=AB,
∴∠B=∠D;
(2)解:设BC=x,则AC=x﹣2,
在Rt△ABC中,AC2+BC2=AB2,
∴(x﹣2)2+x2=42,
解得:x1=1+,x2=1﹣(舍去),
∵∠B=∠E,∠B=∠D,
∴∠D=∠E,
∴CD=CE,
∵CD=CB,
∴CE=CB=1+.
同课章节目录
