九年级数学上24.2.2直线和圆的位置关系(3)同步测试(含答案)
文档属性
| 名称 | 九年级数学上24.2.2直线和圆的位置关系(3)同步测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 121.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-01 06:50:41 | ||
图片预览



文档简介
《24.2.2
直线和圆的位置关系》(3)
一、选择题
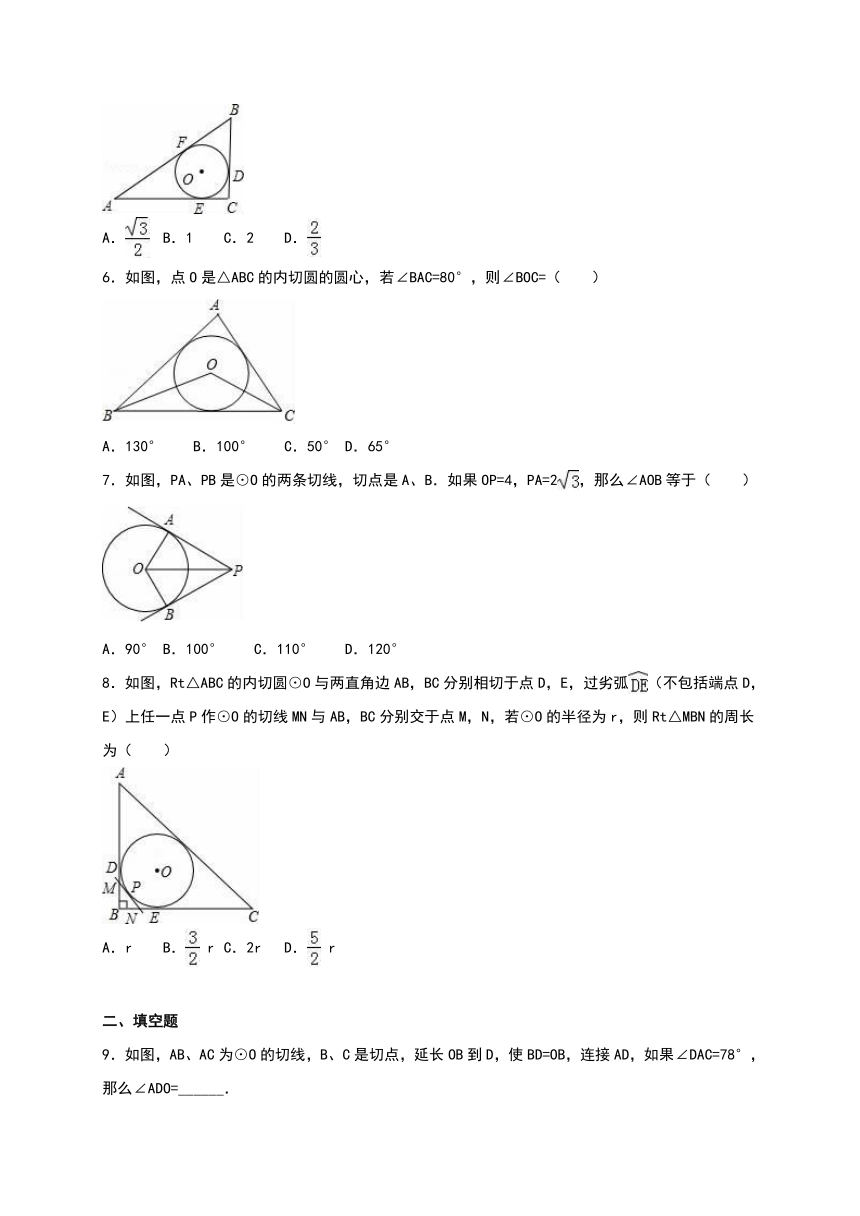
1.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )
A.4
B.8
C.
D.
2.如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=60°,则∠P的度数为( )
A.120°
B.90°
C.60°
D.75°
3.如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( )
A.12
B.6
C.8
D.4
4.如图,边长为a的正三角形的内切圆半径是( )
A.
B.
C.
D.
5.在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是( )
A.
B.1
C.2
D.
6.如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,则∠BOC=( )
A.130°
B.100°
C.50°
D.65°
7.如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=2,那么∠AOB等于( )
A.90°
B.100°
C.110°
D.120°
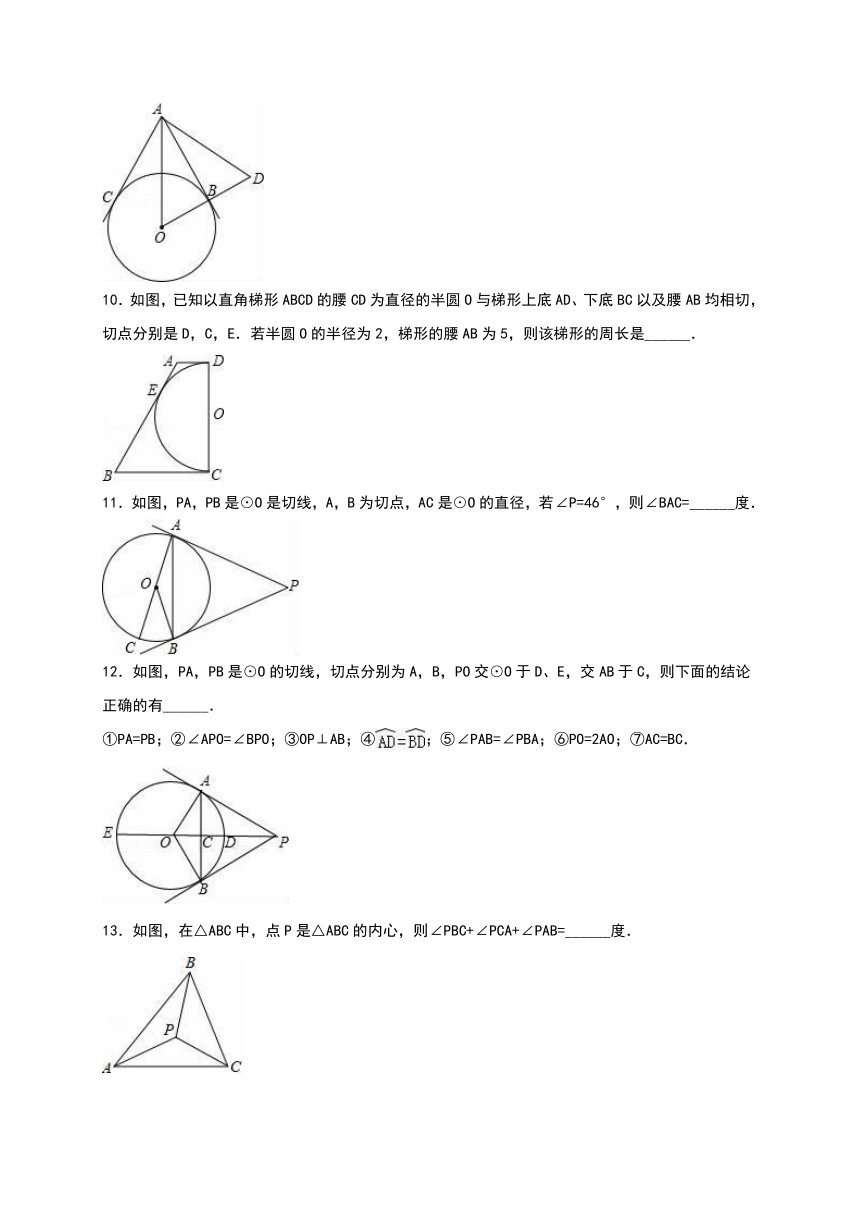
8.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
A.r
B.
r
C.2r
D.
r
二、填空题
9.如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO=______.
10.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是______.
11.如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则∠BAC=______度.
12.如图,PA,PB是⊙O的切线,切点分别为A,B,PO交⊙O于D、E,交AB于C,则下面的结论正确的有______.
①PA=PB;②∠APO=∠BPO;③OP⊥AB;④;⑤∠PAB=∠PBA;⑥PO=2AO;⑦AC=BC.
13.如图,在△ABC中,点P是△ABC的内心,则∠PBC+∠PCA+∠PAB=______度.
14.P为⊙O外一点,PA,PB分别切⊙O于点A,B,∠APB=50°,点C为⊙O上一点(不与A,B重合),则∠ACB的度数为______.
15.如图,点O为△ABC的外心,点I为△ABC的内心,若∠BOC=140°,则∠BIC的度数为______.
《24.2.2
直线和圆的位置关系》(3)
参考答案与试题解析
一、选择题
1.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )
A.4
B.8
C.
D.
【解答】解:∵PA、PB都是⊙O的切线,
∴PA=PB,
又∵∠P=60°,
∴△PAB是等边三角形,即AB=PA=8,
故选B.
2.如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=60°,则∠P的度数为( )
A.120°
B.90°
C.60°
D.75°
【解答】解:连接OA、OB.
在四边形PAOB中,由于PA、PB分别切⊙O于点A、B,
则∠OAP=∠OBP=90°,
又∠AOB=2∠E=120°,
∠P=60°.
故选C.
3.如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( )
A.12
B.6
C.8
D.4
【解答】解:∵PA,PB分别和⊙O切于A,B两点,
∴PA=PB,
∵DE是⊙O的切线,
∴DA=DC,EB=EC,
∵△PDE的周长为12,
即PD+DE+PE=PD+DC+EC+PE=PD+AD+EB+PE=PA+PB=2PA=12,
∴PA=6.
故选B.
4.如图,边长为a的正三角形的内切圆半径是( )
A.
B.
C.
D.
【解答】解:∵内切圆的半径、外接圆的半径和半边组成一个30°的直角三角形,
∴∠OBD=30°,BD=,
∴tan∠BOD==,
∴内切圆半径OD=×=a.
故选:A.
5.在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是( )
A.
B.1
C.2
D.
【解答】解:在Rt△ABC,∠C=90°,BC=3,AC=4;
根据勾股定理AB==5;
若设Rt△ABC的内切圆的半径为R,则有:
R==1.故选B.
6.如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,则∠BOC=( )
A.130°
B.100°
C.50°
D.65°
【解答】解:∵OB、OC是∠ABC、∠ACB的角平分线,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣80°)=50°,
∴∠BOC=180°﹣50°=130°.
故选A.
7.如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=2,那么∠AOB等于( )
A.90°
B.100°
C.110°
D.120°
【解答】解:∵△APO≌△BPO(HL),
∴∠AOP=∠BOP.
∵sin∠AOP=AP:OP=2:4=:2,
∴∠AOP=60°.
∴∠AOB=120°.
故选D.
8.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
A.r
B.
r
C.2r
D.
r
【解答】解:连接OD、OE,
∵⊙O是Rt△ABC的内切圆,
∴OD⊥AB,OE⊥BC,
∵∠ABC=90°,
∴∠ODB=∠DBE=∠OEB=90°,
∴四边形ODBE是矩形,
∵OD=OE,
∴矩形ODBE是正方形,
∴BD=BE=OD=OE=r,
∵⊙O切AB于D,切BC于E,切MN于P,NP与NE是从一点出发的圆的两条切线,
∴MP=DM,NP=NE,
∴Rt△MBN的周长为:MB+NB+MN=MB+BN+NE+DM=BD+BE=r+r=2r,
故选C.
二、填空题
9.如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO= 64° .
【解答】解:∵AB、AC为⊙O的切线,
∴∠BAO=∠CAO,OB⊥AB,
∵BD=OB,
∴△AOD为等腰三角形,
∴∠BAO=∠BAD,
∴∠CAO=∠BAO=∠BAD,
∵∠DAC=∠BAD+∠BAO+∠CAO=78°,
∴3∠BAD=78°,解得∠BAD=26°,
∴∠ADO=90°﹣∠BAD=90°﹣26°=64°.
故答案为64°.
10.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是 14 .
【解答】解:根据切线长定理,得AD=AE,BC=BE,所以梯形的周长是5×2+4=14,
故答案为:14.
11.如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则∠BAC= 23 度.
【解答】解:∵PA,PB是⊙O是切线,
∴PA=PB,又∠P=46°,
∴∠PAB=∠PBA==67°,
又PA是⊙O是切线,AO为半径,
∴OA⊥AP,
∴∠OAP=90°,
∴∠BAC=∠OAP﹣∠PAB=90°﹣67°=23°.
故答案为:23
12.如图,PA,PB是⊙O的切线,切点分别为A,B,PO交⊙O于D、E,交AB于C,则下面的结论正确的有 ①②③④⑤⑦ .
①PA=PB;②∠APO=∠BPO;③OP⊥AB;④;⑤∠PAB=∠PBA;⑥PO=2AO;⑦AC=BC.
【解答】解:∵PA,PB是⊙O的切线,
∴PA=PB,所以①正确;
∠APO=∠BPO,所以②正确;
∴OP⊥AB,所以③正确;
∴=,所以④正确;
∵PA=PB,
∴∠PAB=∠PBA,所以⑤正确;
AC=BC,所以⑦正确;
∵PA是⊙O的切线,
∴OA⊥PA,
∴∠PAO=90°,
∴只有当∠APO=30°时,PO=2AO,所以⑥错误.
故答案为①②③④⑤⑦.
13.如图,在△ABC中,点P是△ABC的内心,则∠PBC+∠PCA+∠PAB= 90 度.
【解答】解:∵点P是△ABC的内心,
∴PB平分∠ABC,PA平分∠BAC,PC平分∠ACB,
∵∠ABC+∠ACB+∠BAC=180°,
∴∠PBC+∠PCA+∠PAB=90°,
故答案为:90°
14.P为⊙O外一点,PA,PB分别切⊙O于点A,B,∠APB=50°,点C为⊙O上一点(不与A,B重合),则∠ACB的度数为 65°或115° .
【解答】解:连接OA、OB.
∵PA,PB分别切⊙O于点A,B,
∴OA⊥PA,OB⊥PB;
∴∠PAO=∠PBO=90°;
又∵∠APB=50°,
∴在四边形AOBP中,∠AOB=360°﹣90°﹣90°﹣50°=130°,
∴∠ADB=×∠AOB=×130°=65°,
即当C在D处时,∠ACB=65°.
在四边形ADBC中,∠ACB=180°﹣∠ADB=180°﹣65°=115°.
于是∠ACB的度数为65°或115°.
15.如图,点O为△ABC的外心,点I为△ABC的内心,若∠BOC=140°,则∠BIC的度数为 125° .
【解答】解:∵点O为△ABC的外心,∠BOC=140°,
∴∠A=70°,
∴∠ABC+∠ACB=110°,
∵点I为△ABC的内心,
∴∠IBC+∠ICB=55°,
∴∠BIC=125°.
故答案为:125°.
直线和圆的位置关系》(3)
一、选择题
1.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )
A.4
B.8
C.
D.
2.如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=60°,则∠P的度数为( )
A.120°
B.90°
C.60°
D.75°
3.如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( )
A.12
B.6
C.8
D.4
4.如图,边长为a的正三角形的内切圆半径是( )
A.
B.
C.
D.
5.在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是( )
A.
B.1
C.2
D.
6.如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,则∠BOC=( )
A.130°
B.100°
C.50°
D.65°
7.如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=2,那么∠AOB等于( )
A.90°
B.100°
C.110°
D.120°
8.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
A.r
B.
r
C.2r
D.
r
二、填空题
9.如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO=______.
10.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是______.
11.如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则∠BAC=______度.
12.如图,PA,PB是⊙O的切线,切点分别为A,B,PO交⊙O于D、E,交AB于C,则下面的结论正确的有______.
①PA=PB;②∠APO=∠BPO;③OP⊥AB;④;⑤∠PAB=∠PBA;⑥PO=2AO;⑦AC=BC.
13.如图,在△ABC中,点P是△ABC的内心,则∠PBC+∠PCA+∠PAB=______度.
14.P为⊙O外一点,PA,PB分别切⊙O于点A,B,∠APB=50°,点C为⊙O上一点(不与A,B重合),则∠ACB的度数为______.
15.如图,点O为△ABC的外心,点I为△ABC的内心,若∠BOC=140°,则∠BIC的度数为______.
《24.2.2
直线和圆的位置关系》(3)
参考答案与试题解析
一、选择题
1.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )
A.4
B.8
C.
D.
【解答】解:∵PA、PB都是⊙O的切线,
∴PA=PB,
又∵∠P=60°,
∴△PAB是等边三角形,即AB=PA=8,
故选B.
2.如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=60°,则∠P的度数为( )
A.120°
B.90°
C.60°
D.75°
【解答】解:连接OA、OB.
在四边形PAOB中,由于PA、PB分别切⊙O于点A、B,
则∠OAP=∠OBP=90°,
又∠AOB=2∠E=120°,
∠P=60°.
故选C.
3.如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( )
A.12
B.6
C.8
D.4
【解答】解:∵PA,PB分别和⊙O切于A,B两点,
∴PA=PB,
∵DE是⊙O的切线,
∴DA=DC,EB=EC,
∵△PDE的周长为12,
即PD+DE+PE=PD+DC+EC+PE=PD+AD+EB+PE=PA+PB=2PA=12,
∴PA=6.
故选B.
4.如图,边长为a的正三角形的内切圆半径是( )
A.
B.
C.
D.
【解答】解:∵内切圆的半径、外接圆的半径和半边组成一个30°的直角三角形,
∴∠OBD=30°,BD=,
∴tan∠BOD==,
∴内切圆半径OD=×=a.
故选:A.
5.在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是( )
A.
B.1
C.2
D.
【解答】解:在Rt△ABC,∠C=90°,BC=3,AC=4;
根据勾股定理AB==5;
若设Rt△ABC的内切圆的半径为R,则有:
R==1.故选B.
6.如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,则∠BOC=( )
A.130°
B.100°
C.50°
D.65°
【解答】解:∵OB、OC是∠ABC、∠ACB的角平分线,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣80°)=50°,
∴∠BOC=180°﹣50°=130°.
故选A.
7.如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=2,那么∠AOB等于( )
A.90°
B.100°
C.110°
D.120°
【解答】解:∵△APO≌△BPO(HL),
∴∠AOP=∠BOP.
∵sin∠AOP=AP:OP=2:4=:2,
∴∠AOP=60°.
∴∠AOB=120°.
故选D.
8.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
A.r
B.
r
C.2r
D.
r
【解答】解:连接OD、OE,
∵⊙O是Rt△ABC的内切圆,
∴OD⊥AB,OE⊥BC,
∵∠ABC=90°,
∴∠ODB=∠DBE=∠OEB=90°,
∴四边形ODBE是矩形,
∵OD=OE,
∴矩形ODBE是正方形,
∴BD=BE=OD=OE=r,
∵⊙O切AB于D,切BC于E,切MN于P,NP与NE是从一点出发的圆的两条切线,
∴MP=DM,NP=NE,
∴Rt△MBN的周长为:MB+NB+MN=MB+BN+NE+DM=BD+BE=r+r=2r,
故选C.
二、填空题
9.如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO= 64° .
【解答】解:∵AB、AC为⊙O的切线,
∴∠BAO=∠CAO,OB⊥AB,
∵BD=OB,
∴△AOD为等腰三角形,
∴∠BAO=∠BAD,
∴∠CAO=∠BAO=∠BAD,
∵∠DAC=∠BAD+∠BAO+∠CAO=78°,
∴3∠BAD=78°,解得∠BAD=26°,
∴∠ADO=90°﹣∠BAD=90°﹣26°=64°.
故答案为64°.
10.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是 14 .
【解答】解:根据切线长定理,得AD=AE,BC=BE,所以梯形的周长是5×2+4=14,
故答案为:14.
11.如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则∠BAC= 23 度.
【解答】解:∵PA,PB是⊙O是切线,
∴PA=PB,又∠P=46°,
∴∠PAB=∠PBA==67°,
又PA是⊙O是切线,AO为半径,
∴OA⊥AP,
∴∠OAP=90°,
∴∠BAC=∠OAP﹣∠PAB=90°﹣67°=23°.
故答案为:23
12.如图,PA,PB是⊙O的切线,切点分别为A,B,PO交⊙O于D、E,交AB于C,则下面的结论正确的有 ①②③④⑤⑦ .
①PA=PB;②∠APO=∠BPO;③OP⊥AB;④;⑤∠PAB=∠PBA;⑥PO=2AO;⑦AC=BC.
【解答】解:∵PA,PB是⊙O的切线,
∴PA=PB,所以①正确;
∠APO=∠BPO,所以②正确;
∴OP⊥AB,所以③正确;
∴=,所以④正确;
∵PA=PB,
∴∠PAB=∠PBA,所以⑤正确;
AC=BC,所以⑦正确;
∵PA是⊙O的切线,
∴OA⊥PA,
∴∠PAO=90°,
∴只有当∠APO=30°时,PO=2AO,所以⑥错误.
故答案为①②③④⑤⑦.
13.如图,在△ABC中,点P是△ABC的内心,则∠PBC+∠PCA+∠PAB= 90 度.
【解答】解:∵点P是△ABC的内心,
∴PB平分∠ABC,PA平分∠BAC,PC平分∠ACB,
∵∠ABC+∠ACB+∠BAC=180°,
∴∠PBC+∠PCA+∠PAB=90°,
故答案为:90°
14.P为⊙O外一点,PA,PB分别切⊙O于点A,B,∠APB=50°,点C为⊙O上一点(不与A,B重合),则∠ACB的度数为 65°或115° .
【解答】解:连接OA、OB.
∵PA,PB分别切⊙O于点A,B,
∴OA⊥PA,OB⊥PB;
∴∠PAO=∠PBO=90°;
又∵∠APB=50°,
∴在四边形AOBP中,∠AOB=360°﹣90°﹣90°﹣50°=130°,
∴∠ADB=×∠AOB=×130°=65°,
即当C在D处时,∠ACB=65°.
在四边形ADBC中,∠ACB=180°﹣∠ADB=180°﹣65°=115°.
于是∠ACB的度数为65°或115°.
15.如图,点O为△ABC的外心,点I为△ABC的内心,若∠BOC=140°,则∠BIC的度数为 125° .
【解答】解:∵点O为△ABC的外心,∠BOC=140°,
∴∠A=70°,
∴∠ABC+∠ACB=110°,
∵点I为△ABC的内心,
∴∠IBC+∠ICB=55°,
∴∠BIC=125°.
故答案为:125°.
同课章节目录
