沪科版九年级数学下册24.3.1圆周角定理测试卷(解析版)
文档属性
| 名称 | 沪科版九年级数学下册24.3.1圆周角定理测试卷(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 337.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-01 20:57:28 | ||
图片预览


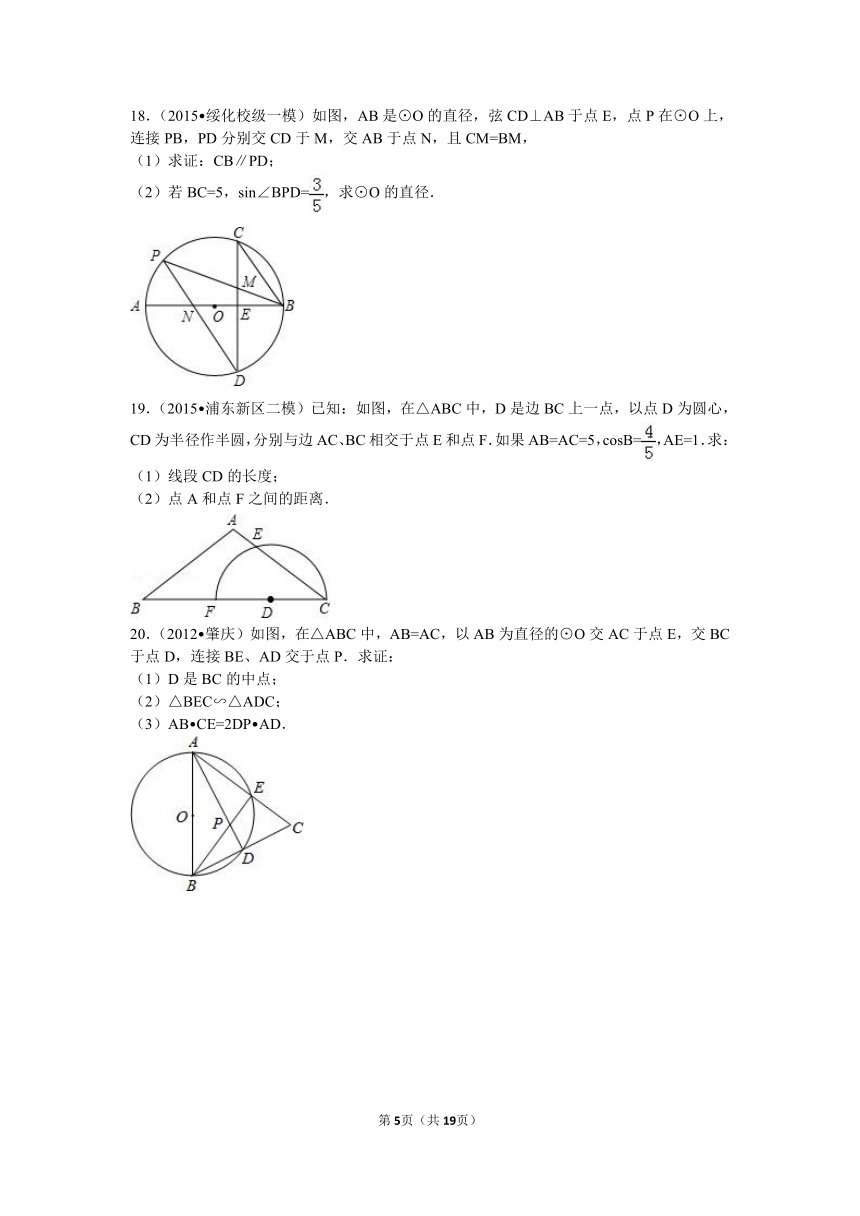
文档简介
沪科版九年级数学下册24.3.1《圆周角定理》测试卷
一.选择题(共10小题)
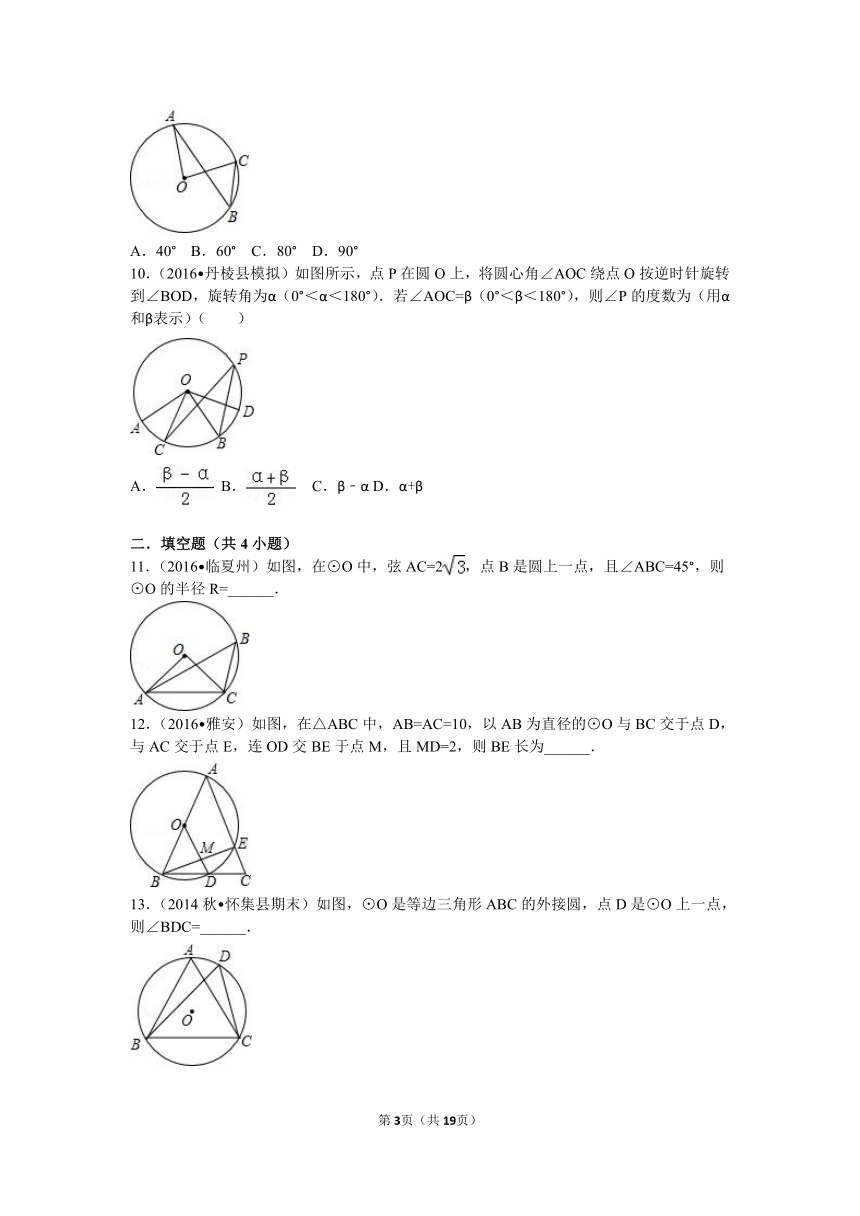
1.(2016 张家界)如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
A.75°
B.60°
C.45°
D.30°
2.(2016 邗江区二模)如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA,OB在0点钉在一起,并使它们保持垂直,在测直径时,把0点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )
A.12个单位
B.10个单位
C.4个单位
D.15个单位
3.(2016 黔东南州一模)如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )
A.25°
B.30°
C.40°
D.50°
4.(2016 盘龙区一模)如图,AB是⊙O的直径,CD是⊙O的弦.若∠BAC=23°,则∠ADC的大小为( )
A.23°
B.57°
C.67°
D.77°
5.(2016 嘉善县模拟)如图,AB是⊙O的弦,点C在圆上,已知∠OBA=40°,则∠C=( )
A.40°
B.50°
C.60°
D.80°
6.(2016 河南模拟)如图,⊙O的直径BD=4,∠A=60°,则BC的长度为( )
A.
B.2
C.2
D.4
7.(2016 丰润区二模)如图,已知AB、AD是⊙O的弦,∠B=30°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=20°,则∠BAD的度数是( )
A.30°
B.40°
C.50°
D.60°
8.(2016 峄城区一模)在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
A.35°
B.40°
C.45°
D.65°
9.(2016 重庆模拟)如图,点A、点B、点C均在⊙O上,若∠B=40°,则∠AOC的度数为( )
A.40°
B.60°
C.80°
D.90°
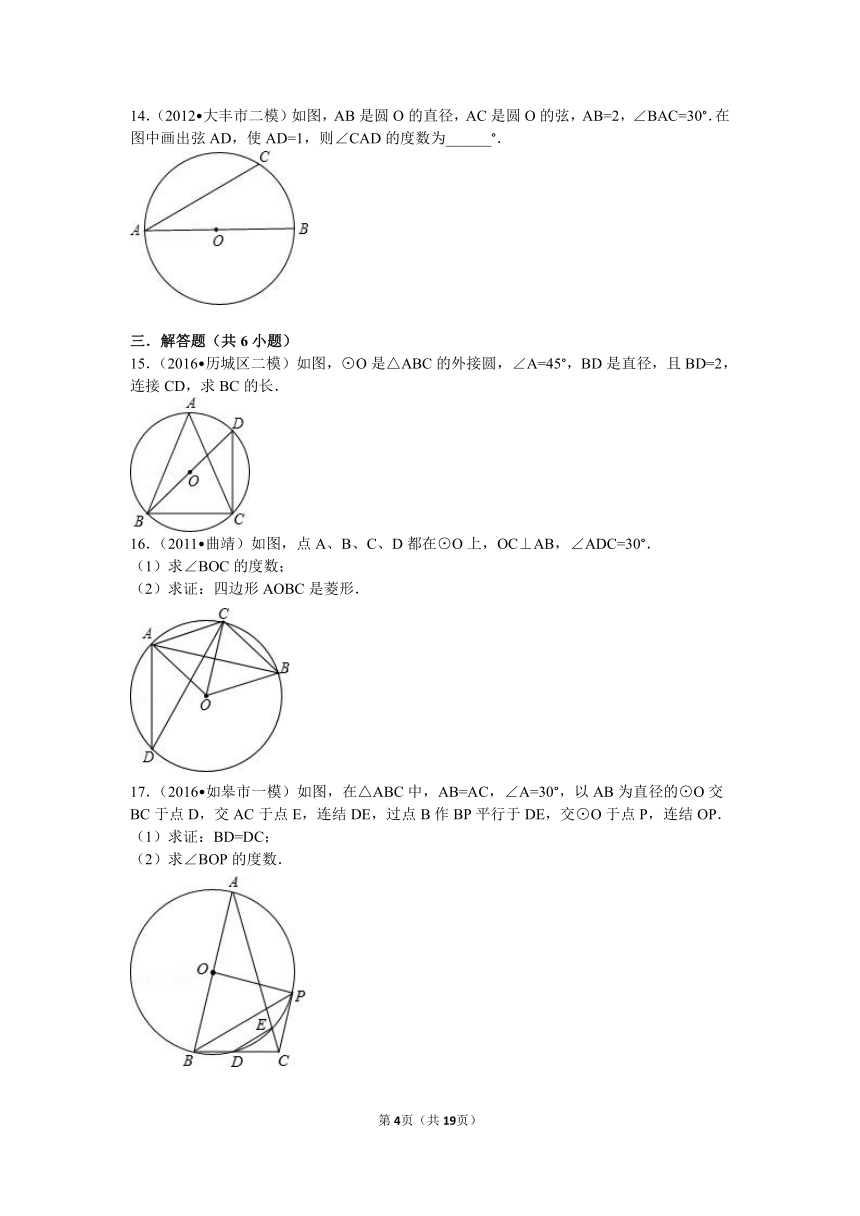
10.(2016 丹棱县模拟)如图所示,点P在圆O上,将圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°).若∠AOC=β(0°<β<180°),则∠P的度数为(用α和β表示)( )
A.
B.
C.β﹣α
D.α+β
二.填空题(共4小题)
11.(2016 临夏州)如图,在⊙O中,弦AC=2,点B是圆上一点,且∠ABC=45°,则⊙O的半径R=______.
12.(2016 雅安)如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且MD=2,则BE长为______.
13.(2014秋 怀集县期末)如图,⊙O是等边三角形ABC的外接圆,点D是⊙O上一点,则∠BDC=______.
14.(2012 大丰市二模)如图,AB是圆O的直径,AC是圆O的弦,AB=2,∠BAC=30°.在图中画出弦AD,使AD=1,则∠CAD的度数为______°.
三.解答题(共6小题)
15.(2016 历城区二模)如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,且BD=2,连接CD,求BC的长.
16.(2011 曲靖)如图,点A、B、C、D都在⊙O上,OC⊥AB,∠ADC=30°.
(1)求∠BOC的度数;
(2)求证:四边形AOBC是菱形.
17.(2016 如皋市一模)如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点B作BP平行于DE,交⊙O于点P,连结OP.
(1)求证:BD=DC;
(2)求∠BOP的度数.
18.(2015 绥化校级一模)如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,连接PB,PD分别交CD于M,交AB于点N,且CM=BM,
(1)求证:CB∥PD;
(2)若BC=5,sin∠BPD=,求⊙O的直径.
19.(2015 浦东新区二模)已知:如图,在△ABC中,D是边BC上一点,以点D为圆心,CD为半径作半圆,分别与边AC、BC相交于点E和点F.如果AB=AC=5,cosB=,AE=1.求:
(1)线段CD的长度;
(2)点A和点F之间的距离.
20.(2012 肇庆)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE、AD交于点P.求证:
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)AB CE=2DP AD.
沪科版九年级数学下册24.3.1《圆周角定理》测试卷
参考答案与试题解析
一.选择题(共10小题)
1.(2016 张家界)如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
A.75°
B.60°
C.45°
D.30°
【分析】根据AB是⊙O的直径可得出∠ACB=90°,再根据三角形内角和为180°以及∠OBC=60°,即可求出∠BAC的度数.
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠OBC=60°,
∴∠BAC=180°﹣∠ACB﹣∠ABC=30°.
故选D.
【点评】本题考查了圆周角定理以及角的计算,解题的关键是找出∠ACB=90°.本题属于基础题,难度不大,解决该题型题目时,找出直径所对的圆周角为90°是关键.
2.(2016 邗江区二模)如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA,OB在0点钉在一起,并使它们保持垂直,在测直径时,把0点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )
A.12个单位
B.10个单位
C.4个单位
D.15个单位
【分析】根据圆中的有关性质“90°的圆周角所对的弦是直径”.从而得到EF即可是直径,根据勾股定理计算即可.
【解答】解:连接EF,
∵OE⊥OF,
∴EF是直径,
∴EF====10.
故选:B.
【点评】考查了圆中的有关性质:90°的圆周角所对的弦是直径.此性质是判断直径的一个有效方法,也是构造直角三角形的一个常用方法.
3.(2016 黔东南州一模)如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )
A.25°
B.30°
C.40°
D.50°
【分析】先根据平行线的性质求出∠AOD的度数,再由圆周角定理即可解答.
【解答】解:∵OA∥DE,∠D=50°,∴∠AOD=50°,
∵∠C=∠AOD,
∠C=×50°=25°.
故选A.
【点评】本题比较简单.考查的是平行线的性质及圆周角定理.
4.(2016 盘龙区一模)如图,AB是⊙O的直径,CD是⊙O的弦.若∠BAC=23°,则∠ADC的大小为( )
A.23°
B.57°
C.67°
D.77°
【分析】由AB是⊙O的直径,根据半圆(或直径)所对的圆周角是直角,即可求得∠ACB=90°,又由∠BAC=23°,即可求得∠B的度数,然后根据在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得∠ADC的大小.
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=23°,
∴∠B=90°﹣∠BAC=67°,
∴∠ADC=∠B=67°.
故C.
【点评】本题考查圆周角定理及直角三角形的性质.此题属容易题,解题的关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角相等与半圆(或直径)所对的圆周角是直角定理的应用.
5.(2016 嘉善县模拟)如图,AB是⊙O的弦,点C在圆上,已知∠OBA=40°,则∠C=( )
A.40°
B.50°
C.60°
D.80°
【分析】首先根据等边对等角即可求得∠OAB的度数,然后根据三角形的内角和定理求得∠AOB的度数,再根据圆周角定理即可求解.
【解答】解:∵OA=OB,
∴∠OAB=∠OBA=40°,
∴∠AOB=180°﹣40°﹣40°=100°.
∴∠C=∠AOB=×100°=50°.
故选B.
【点评】本题考查了等腰三角形的性质定理以及圆周角定理,正确理解定理是关键.
6.(2016 河南模拟)如图,⊙O的直径BD=4,∠A=60°,则BC的长度为( )
A.
B.2
C.2
D.4
【分析】根据圆周角定理得∠BCD=90°,∠D=∠A=60°,然后利用∠D的正弦计算BC的长.
【解答】解:∵BD为直径,
∴∠BCD=90°,
∵∠D=∠A=60°,
∴sinD=sin60°=,
∴BC=4×=2.
故选C.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
7.(2016 丰润区二模)如图,已知AB、AD是⊙O的弦,∠B=30°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=20°,则∠BAD的度数是( )
A.30°
B.40°
C.50°
D.60°
【分析】连接OA,根据圆的半径相等证明∠OAB=∠B和∠OAD=∠D,得到答案.
【解答】解:连接OA,
∵OA=OB,
∴∠OAB=∠B=30°,
∵OA=OD,
∴∠OAD=∠D=20°,
∴∠BAD=∠OAB+∠OAD=50°,
故选:C.
【点评】本题考查的是圆的性质和等腰三角形的性质,掌握圆的半径相等和等边对等角是解题的关键.
8.(2016 峄城区一模)在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
A.35°
B.40°
C.45°
D.65°
【分析】首先连接BC,由AB是直径,可求得∠ACB=90°,则可求得∠B的度数,然后由翻折的性质可得,所对的圆周角为∠B,所对的圆周角为∠ADC,继而求得答案.
【解答】解:连接BC,
∵AB是直径,
∴∠ACB=90°,
∵∠BAC=25°,
∴∠B=90°﹣∠BAC=90°﹣25°=65°,
根据翻折的性质,所对的圆周角为∠B,所对的圆周角为∠ADC,
∴∠ADC+∠B=180°,
∴∠B=∠CDB=65°,
∴∠DCA=∠CDB﹣∠A=65°﹣25°=40°.
故选B.
【点评】此题考查了圆周角定理以及折叠的性质.注意掌握辅助线的作法,能得到∠BDC=∠B是解此题的关键.
9.(2016 重庆模拟)如图,点A、点B、点C均在⊙O上,若∠B=40°,则∠AOC的度数为( )
A.40°
B.60°
C.80°
D.90°
【分析】直接根据圆周角定理求解.
【解答】解:∵∠B=40°,
∴∠AOC=2∠B=80°.
故选C.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
10.(2016 丹棱县模拟)如图所示,点P在圆O上,将圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°).若∠AOC=β(0°<β<180°),则∠P的度数为(用α和β表示)( )
A.
B.
C.β﹣α
D.α+β
【分析】根据圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°)可知∠AOB=α,再由∠AOC=β可求出∠COB的度数,根据圆周角定理即可求出∠P的度数.
【解答】解:∵圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°),
∴∠AOB=α,
∵∠AOC=β,
∴∠COB=α﹣β,
∴∠P==.
故选A.
【点评】本题考查的是圆周角定理及图形的旋转,解答此题的关键是弄清旋转角即为∠AOB的度数.
二.填空题(共4小题)
11.(2016 临夏州)如图,在⊙O中,弦AC=2,点B是圆上一点,且∠ABC=45°,则⊙O的半径R= .
【分析】通过∠ABC=45°,可得出∠AOC=90°,根据OA=OC就可以结合勾股定理求出AC的长了.
【解答】解:∵∠ABC=45°,
∴∠AOC=90°,
∵OA=OC=R,
∴R2+R2=2,
解得R=.
故答案为:.
【点评】本题考查了圆周角定理、勾股定理,解题的关键是通过圆周角定理得到∠AOC的度数.
12.(2016 雅安)如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且MD=2,则BE长为 8 .
【分析】连接AD,由圆周角定理得出∠AEB=∠ADB=90°,由等腰三角形的性质得出BD=CD,由三角形中位线定理得出OD∥AC,CE=2MD=4,求出AE,再由勾股定理求出BE即可.
【解答】解:连接AD,如图所示:
∵以AB为直径的⊙O与BC交于点D,
∴∠AEB=∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
∵OA=OB,
∴OD∥AC,
∴BM=EM,
∴CE=2MD=4,
∴AE=AC﹣CE=6,
∴BE==;
故答案为:8.
【点评】本题考查了圆周角定理、等腰三角形的性质、勾股定理、三角形中位线定理;熟练掌握圆周角定理,由三角形中位线定理求出CE是解决问题的关键.
13.(2014秋 怀集县期末)如图,⊙O是等边三角形ABC的外接圆,点D是⊙O上一点,则∠BDC= 60° .
【分析】因为⊙O是等边三角形ABC的外接圆,所以∠A=∠ABC=∠ACB=60°,所以∠BCD=∠A=60°.
【解答】解:∵⊙O是等边三角形ABC的外接圆,
∴∠A=∠ABC=∠ACB=60°,
∴∠BDC=∠A=60°.
【点评】此题主要考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
14.(2012 大丰市二模)如图,AB是圆O的直径,AC是圆O的弦,AB=2,∠BAC=30°.在图中画出弦AD,使AD=1,则∠CAD的度数为 30或90 °.
【分析】根据题意作图,由AB是圆O的直径,可得∠ADB=∠AD′B=90°,继而可求得∠DAB的度数,则可求得答案.
【解答】解:如图,∵AB是圆O的直径,
∴∠ADB=∠AD′B=90°,
∵AD=AD′=1,AB=2,
∴cos∠DAB=cosD′AB=,
∴∠DAB=∠D′AB=60°,
∵∠CAB=30°,
∴∠CAD=30°,∠CAD′=90°.
∴∠CAD的度数为:30°或90°.
故答案为:30或90.
【点评】此题考查了圆周角定理以及解直角三角形的知识.此题难度适中,注意掌握数形结合思想与分类讨论思想的应用.
三.解答题(共6小题)
15.(2016 历城区二模)如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,且BD=2,连接CD,求BC的长.
【分析】先根据圆周角定理可求出∠D=45°,∠BCD=90°,再根据三角形内角和定理可知△BCD是等腰直角三角形,由锐角三角函数的定义即可求出BC的长.
【解答】解:在⊙O中,∵∠A=45°,∠D=45°,
∵BD为⊙O的直径,
∴∠BCD=90°,
∴△BCD是等腰直角三角形,
∴BC=BD sin45°,
∵BD=2,
∴.
【点评】本题主要考查的是圆周角定理、等腰直角三角形的判定及锐角三角函数的定义,关键是求出△BCD是等腰直角三角形.
16.(2011 曲靖)如图,点A、B、C、D都在⊙O上,OC⊥AB,∠ADC=30°.
(1)求∠BOC的度数;
(2)求证:四边形AOBC是菱形.
【分析】(1)根据垂径定理得出=,再利用圆周角定理得出∠BOC的度数;
(2)根据等边三角形的判定得出BC=BO=CO,进而利用(1)中结论得出AO=BO=AC=BC,即可证明结论.
【解答】(1)解:∵点A、B、C、D都在⊙O上,OC⊥AB,
∴=,
∵∠ADC=30°,
∴∠AOC=∠BOC=2∠ADC=60°,
∴∠BOC的度数为60°;
(2)证明:∵=,
∴AC=BC,
AO=BO,
∵∠BOC的度数为60°,BO=CO
∴△BOC为等边三角形,
∴BC=BO=CO,
∴AO=BO=AC=BC,
∴四边形AOBC是菱形.
【点评】此题主要考查了菱形的判定以及垂径定理和圆周角定理等知识,根据垂径定理得出=是解决问题的关键.
17.(2016 如皋市一模)如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点B作BP平行于DE,交⊙O于点P,连结OP.
(1)求证:BD=DC;
(2)求∠BOP的度数.
【分析】(1)连结AD,根据直径所对的圆周角为直角得到∠ADB=90°,而AB=AC,根据等腰进行的性质即可得到BD=CD;
(2)根据等腰三角形的性质和三角形内角和定理可计算出∠ABC=75°,再根据圆内接四边形的性质得到∠EDC=∠BAC=30°,然后利用平行线的性质得到∠PBC=∠EDC=30°,所以∠OBP=∠ABC﹣∠PBC=45°,于是可判断△OBP为等腰直角三角形,则∠BOP=90°.
【解答】(1)证明:连结AD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD;
(2)解:∵∠BAC=30°,AB=AC,
∴∠ABC=(180°﹣30°)=75°,
∵四边形ABDE为圆O的内接四边形,
∴∠EDC=∠BAC=30°,
∵BP∥DE,
∴∠PBC=∠EDC=30°,
∴∠OBP=∠ABC﹣∠PBC=45°,
∵OB=OP,
∴△OBP为等腰直角三角形,
∴∠BOP=90°.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.也考查了等腰三角形的性质.
18.(2015 绥化校级一模)如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,连接PB,PD分别交CD于M,交AB于点N,且CM=BM,
(1)求证:CB∥PD;
(2)若BC=5,sin∠BPD=,求⊙O的直径.
【分析】(1)由等腰三角形的性质和圆周角定理得出∠P=∠C,然后根据平行线的判定定理即可得到结论;
(2)连接AC,根据垂径定理及圆周角定理得到∠P=∠A,∠ACB=90°,则sinA=sinP,然后根据正弦的定义得到==,得出AB的长即可.
【解答】(1)证明:∵CM=BM,
∴∠C=∠CBM,
∵∠C=∠P,
∴∠P=∠CBM,
∴CB∥PD;
(2)解:连接AC,如图所示
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴,
∴∠BPD=∠A,
∴sinA=sin∠BPD=,
又∵AB为直径,
∴∠ACB=90°,
∴sinA==,即=,
解得:AB=,
即⊙O的直径为.
【点评】本题考查了圆的综合题:在同圆或等圆中,相等的弧所对的圆周角相等,直径所对的圆周角为直角;垂直于弦的直径平分弦,并且平分弦所对的弧;运用相似三角形的判定与性质证明线段之间的关系;运用正弦的定义进行几何计算.
19.(2015 浦东新区二模)已知:如图,在△ABC中,D是边BC上一点,以点D为圆心,CD为半径作半圆,分别与边AC、BC相交于点E和点F.如果AB=AC=5,cosB=,AE=1.求:
(1)线段CD的长度;
(2)点A和点F之间的距离.
【分析】(1)连接EF,利用圆周角定理得出∠FEC=90°,再利用等腰三角形的性质,结合锐角三角函数得出答案;
(2)利用锐角三角函数得出NC的长,再利用勾股定理得出答案.
【解答】解:(1)连接EF,
∵由题意可得FC是⊙D的直径,
∴∠FEC=90°,
∵AB=AC,
∴∠B=∠ACB,
∵AB=AC=5,cosB=,AE=1,
∴EC=4,cosB=cos∠ACB===,
解得:FC=5,
则DC=2.5;
(2)连接AF,过点A作AN⊥BC于点N,
∵AB=5,cosB=,
∴BN=4,
∴AN=3,
∵cosC=cosB=,
∴NC=4,
∴FN=1,
∴AF==.
【点评】此题主要考查了圆周角定理以及勾股定理和锐角三角函数等知识,正确应用锐角三角函数关系是解题关键.
20.(2012 肇庆)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE、AD交于点P.求证:
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)AB CE=2DP AD.
【分析】(1)由AB是⊙O的直径,可得AD⊥BC,又由AB=AC,由三线合一,即可证得D是BC的中点;
(2)由AB是⊙O的直径,∠AEB=∠ADB=90°,又由∠C是公共角,即可证得△BEC∽△ADC;
(3)易证得△ABD∽△BCE与△BPD∽△BCE,根据相似三角形的对应边成比例与BC=2BD,即可证得AB CE=2DP AD.
【解答】证明:(1)∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴D是BC的中点;
(2)∵AB是⊙O的直径,
∴∠AEB=∠ADB=90°,
即∠CEB=∠CDA=90°,
∵∠C是公共角,
∴△BEC∽△ADC;
(3)∵△BEC∽△ADC,
∴∠CBE=∠CAD,
∵AB=AC,BD=CD,
∴∠BAD=∠CAD,
∴∠BAD=∠CBE,
∵∠ADB=∠BEC=90°,
∴△ABD∽△BCE,
∴,
∴,
∵∠BDP=∠BEC=90°,∠PBD=∠CBE,
∴△BPD∽△BCE,
∴=,
∵BC=2BD,∴AB:AD=2BD:BE,
∴,
∴AB CE=2DP AD.
【点评】此题考查了相似三角形的判定与性质、圆周角定理以及等腰三角形的性质.此题难度适中,注意数形结合思想的应用.
第6页(共19页)
一.选择题(共10小题)
1.(2016 张家界)如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
A.75°
B.60°
C.45°
D.30°
2.(2016 邗江区二模)如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA,OB在0点钉在一起,并使它们保持垂直,在测直径时,把0点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )
A.12个单位
B.10个单位
C.4个单位
D.15个单位
3.(2016 黔东南州一模)如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )
A.25°
B.30°
C.40°
D.50°
4.(2016 盘龙区一模)如图,AB是⊙O的直径,CD是⊙O的弦.若∠BAC=23°,则∠ADC的大小为( )
A.23°
B.57°
C.67°
D.77°
5.(2016 嘉善县模拟)如图,AB是⊙O的弦,点C在圆上,已知∠OBA=40°,则∠C=( )
A.40°
B.50°
C.60°
D.80°
6.(2016 河南模拟)如图,⊙O的直径BD=4,∠A=60°,则BC的长度为( )
A.
B.2
C.2
D.4
7.(2016 丰润区二模)如图,已知AB、AD是⊙O的弦,∠B=30°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=20°,则∠BAD的度数是( )
A.30°
B.40°
C.50°
D.60°
8.(2016 峄城区一模)在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
A.35°
B.40°
C.45°
D.65°
9.(2016 重庆模拟)如图,点A、点B、点C均在⊙O上,若∠B=40°,则∠AOC的度数为( )
A.40°
B.60°
C.80°
D.90°
10.(2016 丹棱县模拟)如图所示,点P在圆O上,将圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°).若∠AOC=β(0°<β<180°),则∠P的度数为(用α和β表示)( )
A.
B.
C.β﹣α
D.α+β
二.填空题(共4小题)
11.(2016 临夏州)如图,在⊙O中,弦AC=2,点B是圆上一点,且∠ABC=45°,则⊙O的半径R=______.
12.(2016 雅安)如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且MD=2,则BE长为______.
13.(2014秋 怀集县期末)如图,⊙O是等边三角形ABC的外接圆,点D是⊙O上一点,则∠BDC=______.
14.(2012 大丰市二模)如图,AB是圆O的直径,AC是圆O的弦,AB=2,∠BAC=30°.在图中画出弦AD,使AD=1,则∠CAD的度数为______°.
三.解答题(共6小题)
15.(2016 历城区二模)如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,且BD=2,连接CD,求BC的长.
16.(2011 曲靖)如图,点A、B、C、D都在⊙O上,OC⊥AB,∠ADC=30°.
(1)求∠BOC的度数;
(2)求证:四边形AOBC是菱形.
17.(2016 如皋市一模)如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点B作BP平行于DE,交⊙O于点P,连结OP.
(1)求证:BD=DC;
(2)求∠BOP的度数.
18.(2015 绥化校级一模)如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,连接PB,PD分别交CD于M,交AB于点N,且CM=BM,
(1)求证:CB∥PD;
(2)若BC=5,sin∠BPD=,求⊙O的直径.
19.(2015 浦东新区二模)已知:如图,在△ABC中,D是边BC上一点,以点D为圆心,CD为半径作半圆,分别与边AC、BC相交于点E和点F.如果AB=AC=5,cosB=,AE=1.求:
(1)线段CD的长度;
(2)点A和点F之间的距离.
20.(2012 肇庆)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE、AD交于点P.求证:
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)AB CE=2DP AD.
沪科版九年级数学下册24.3.1《圆周角定理》测试卷
参考答案与试题解析
一.选择题(共10小题)
1.(2016 张家界)如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
A.75°
B.60°
C.45°
D.30°
【分析】根据AB是⊙O的直径可得出∠ACB=90°,再根据三角形内角和为180°以及∠OBC=60°,即可求出∠BAC的度数.
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠OBC=60°,
∴∠BAC=180°﹣∠ACB﹣∠ABC=30°.
故选D.
【点评】本题考查了圆周角定理以及角的计算,解题的关键是找出∠ACB=90°.本题属于基础题,难度不大,解决该题型题目时,找出直径所对的圆周角为90°是关键.
2.(2016 邗江区二模)如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA,OB在0点钉在一起,并使它们保持垂直,在测直径时,把0点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )
A.12个单位
B.10个单位
C.4个单位
D.15个单位
【分析】根据圆中的有关性质“90°的圆周角所对的弦是直径”.从而得到EF即可是直径,根据勾股定理计算即可.
【解答】解:连接EF,
∵OE⊥OF,
∴EF是直径,
∴EF====10.
故选:B.
【点评】考查了圆中的有关性质:90°的圆周角所对的弦是直径.此性质是判断直径的一个有效方法,也是构造直角三角形的一个常用方法.
3.(2016 黔东南州一模)如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )
A.25°
B.30°
C.40°
D.50°
【分析】先根据平行线的性质求出∠AOD的度数,再由圆周角定理即可解答.
【解答】解:∵OA∥DE,∠D=50°,∴∠AOD=50°,
∵∠C=∠AOD,
∠C=×50°=25°.
故选A.
【点评】本题比较简单.考查的是平行线的性质及圆周角定理.
4.(2016 盘龙区一模)如图,AB是⊙O的直径,CD是⊙O的弦.若∠BAC=23°,则∠ADC的大小为( )
A.23°
B.57°
C.67°
D.77°
【分析】由AB是⊙O的直径,根据半圆(或直径)所对的圆周角是直角,即可求得∠ACB=90°,又由∠BAC=23°,即可求得∠B的度数,然后根据在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得∠ADC的大小.
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=23°,
∴∠B=90°﹣∠BAC=67°,
∴∠ADC=∠B=67°.
故C.
【点评】本题考查圆周角定理及直角三角形的性质.此题属容易题,解题的关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角相等与半圆(或直径)所对的圆周角是直角定理的应用.
5.(2016 嘉善县模拟)如图,AB是⊙O的弦,点C在圆上,已知∠OBA=40°,则∠C=( )
A.40°
B.50°
C.60°
D.80°
【分析】首先根据等边对等角即可求得∠OAB的度数,然后根据三角形的内角和定理求得∠AOB的度数,再根据圆周角定理即可求解.
【解答】解:∵OA=OB,
∴∠OAB=∠OBA=40°,
∴∠AOB=180°﹣40°﹣40°=100°.
∴∠C=∠AOB=×100°=50°.
故选B.
【点评】本题考查了等腰三角形的性质定理以及圆周角定理,正确理解定理是关键.
6.(2016 河南模拟)如图,⊙O的直径BD=4,∠A=60°,则BC的长度为( )
A.
B.2
C.2
D.4
【分析】根据圆周角定理得∠BCD=90°,∠D=∠A=60°,然后利用∠D的正弦计算BC的长.
【解答】解:∵BD为直径,
∴∠BCD=90°,
∵∠D=∠A=60°,
∴sinD=sin60°=,
∴BC=4×=2.
故选C.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
7.(2016 丰润区二模)如图,已知AB、AD是⊙O的弦,∠B=30°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=20°,则∠BAD的度数是( )
A.30°
B.40°
C.50°
D.60°
【分析】连接OA,根据圆的半径相等证明∠OAB=∠B和∠OAD=∠D,得到答案.
【解答】解:连接OA,
∵OA=OB,
∴∠OAB=∠B=30°,
∵OA=OD,
∴∠OAD=∠D=20°,
∴∠BAD=∠OAB+∠OAD=50°,
故选:C.
【点评】本题考查的是圆的性质和等腰三角形的性质,掌握圆的半径相等和等边对等角是解题的关键.
8.(2016 峄城区一模)在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
A.35°
B.40°
C.45°
D.65°
【分析】首先连接BC,由AB是直径,可求得∠ACB=90°,则可求得∠B的度数,然后由翻折的性质可得,所对的圆周角为∠B,所对的圆周角为∠ADC,继而求得答案.
【解答】解:连接BC,
∵AB是直径,
∴∠ACB=90°,
∵∠BAC=25°,
∴∠B=90°﹣∠BAC=90°﹣25°=65°,
根据翻折的性质,所对的圆周角为∠B,所对的圆周角为∠ADC,
∴∠ADC+∠B=180°,
∴∠B=∠CDB=65°,
∴∠DCA=∠CDB﹣∠A=65°﹣25°=40°.
故选B.
【点评】此题考查了圆周角定理以及折叠的性质.注意掌握辅助线的作法,能得到∠BDC=∠B是解此题的关键.
9.(2016 重庆模拟)如图,点A、点B、点C均在⊙O上,若∠B=40°,则∠AOC的度数为( )
A.40°
B.60°
C.80°
D.90°
【分析】直接根据圆周角定理求解.
【解答】解:∵∠B=40°,
∴∠AOC=2∠B=80°.
故选C.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
10.(2016 丹棱县模拟)如图所示,点P在圆O上,将圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°).若∠AOC=β(0°<β<180°),则∠P的度数为(用α和β表示)( )
A.
B.
C.β﹣α
D.α+β
【分析】根据圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°)可知∠AOB=α,再由∠AOC=β可求出∠COB的度数,根据圆周角定理即可求出∠P的度数.
【解答】解:∵圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°),
∴∠AOB=α,
∵∠AOC=β,
∴∠COB=α﹣β,
∴∠P==.
故选A.
【点评】本题考查的是圆周角定理及图形的旋转,解答此题的关键是弄清旋转角即为∠AOB的度数.
二.填空题(共4小题)
11.(2016 临夏州)如图,在⊙O中,弦AC=2,点B是圆上一点,且∠ABC=45°,则⊙O的半径R= .
【分析】通过∠ABC=45°,可得出∠AOC=90°,根据OA=OC就可以结合勾股定理求出AC的长了.
【解答】解:∵∠ABC=45°,
∴∠AOC=90°,
∵OA=OC=R,
∴R2+R2=2,
解得R=.
故答案为:.
【点评】本题考查了圆周角定理、勾股定理,解题的关键是通过圆周角定理得到∠AOC的度数.
12.(2016 雅安)如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且MD=2,则BE长为 8 .
【分析】连接AD,由圆周角定理得出∠AEB=∠ADB=90°,由等腰三角形的性质得出BD=CD,由三角形中位线定理得出OD∥AC,CE=2MD=4,求出AE,再由勾股定理求出BE即可.
【解答】解:连接AD,如图所示:
∵以AB为直径的⊙O与BC交于点D,
∴∠AEB=∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
∵OA=OB,
∴OD∥AC,
∴BM=EM,
∴CE=2MD=4,
∴AE=AC﹣CE=6,
∴BE==;
故答案为:8.
【点评】本题考查了圆周角定理、等腰三角形的性质、勾股定理、三角形中位线定理;熟练掌握圆周角定理,由三角形中位线定理求出CE是解决问题的关键.
13.(2014秋 怀集县期末)如图,⊙O是等边三角形ABC的外接圆,点D是⊙O上一点,则∠BDC= 60° .
【分析】因为⊙O是等边三角形ABC的外接圆,所以∠A=∠ABC=∠ACB=60°,所以∠BCD=∠A=60°.
【解答】解:∵⊙O是等边三角形ABC的外接圆,
∴∠A=∠ABC=∠ACB=60°,
∴∠BDC=∠A=60°.
【点评】此题主要考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
14.(2012 大丰市二模)如图,AB是圆O的直径,AC是圆O的弦,AB=2,∠BAC=30°.在图中画出弦AD,使AD=1,则∠CAD的度数为 30或90 °.
【分析】根据题意作图,由AB是圆O的直径,可得∠ADB=∠AD′B=90°,继而可求得∠DAB的度数,则可求得答案.
【解答】解:如图,∵AB是圆O的直径,
∴∠ADB=∠AD′B=90°,
∵AD=AD′=1,AB=2,
∴cos∠DAB=cosD′AB=,
∴∠DAB=∠D′AB=60°,
∵∠CAB=30°,
∴∠CAD=30°,∠CAD′=90°.
∴∠CAD的度数为:30°或90°.
故答案为:30或90.
【点评】此题考查了圆周角定理以及解直角三角形的知识.此题难度适中,注意掌握数形结合思想与分类讨论思想的应用.
三.解答题(共6小题)
15.(2016 历城区二模)如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,且BD=2,连接CD,求BC的长.
【分析】先根据圆周角定理可求出∠D=45°,∠BCD=90°,再根据三角形内角和定理可知△BCD是等腰直角三角形,由锐角三角函数的定义即可求出BC的长.
【解答】解:在⊙O中,∵∠A=45°,∠D=45°,
∵BD为⊙O的直径,
∴∠BCD=90°,
∴△BCD是等腰直角三角形,
∴BC=BD sin45°,
∵BD=2,
∴.
【点评】本题主要考查的是圆周角定理、等腰直角三角形的判定及锐角三角函数的定义,关键是求出△BCD是等腰直角三角形.
16.(2011 曲靖)如图,点A、B、C、D都在⊙O上,OC⊥AB,∠ADC=30°.
(1)求∠BOC的度数;
(2)求证:四边形AOBC是菱形.
【分析】(1)根据垂径定理得出=,再利用圆周角定理得出∠BOC的度数;
(2)根据等边三角形的判定得出BC=BO=CO,进而利用(1)中结论得出AO=BO=AC=BC,即可证明结论.
【解答】(1)解:∵点A、B、C、D都在⊙O上,OC⊥AB,
∴=,
∵∠ADC=30°,
∴∠AOC=∠BOC=2∠ADC=60°,
∴∠BOC的度数为60°;
(2)证明:∵=,
∴AC=BC,
AO=BO,
∵∠BOC的度数为60°,BO=CO
∴△BOC为等边三角形,
∴BC=BO=CO,
∴AO=BO=AC=BC,
∴四边形AOBC是菱形.
【点评】此题主要考查了菱形的判定以及垂径定理和圆周角定理等知识,根据垂径定理得出=是解决问题的关键.
17.(2016 如皋市一模)如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点B作BP平行于DE,交⊙O于点P,连结OP.
(1)求证:BD=DC;
(2)求∠BOP的度数.
【分析】(1)连结AD,根据直径所对的圆周角为直角得到∠ADB=90°,而AB=AC,根据等腰进行的性质即可得到BD=CD;
(2)根据等腰三角形的性质和三角形内角和定理可计算出∠ABC=75°,再根据圆内接四边形的性质得到∠EDC=∠BAC=30°,然后利用平行线的性质得到∠PBC=∠EDC=30°,所以∠OBP=∠ABC﹣∠PBC=45°,于是可判断△OBP为等腰直角三角形,则∠BOP=90°.
【解答】(1)证明:连结AD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD;
(2)解:∵∠BAC=30°,AB=AC,
∴∠ABC=(180°﹣30°)=75°,
∵四边形ABDE为圆O的内接四边形,
∴∠EDC=∠BAC=30°,
∵BP∥DE,
∴∠PBC=∠EDC=30°,
∴∠OBP=∠ABC﹣∠PBC=45°,
∵OB=OP,
∴△OBP为等腰直角三角形,
∴∠BOP=90°.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.也考查了等腰三角形的性质.
18.(2015 绥化校级一模)如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,连接PB,PD分别交CD于M,交AB于点N,且CM=BM,
(1)求证:CB∥PD;
(2)若BC=5,sin∠BPD=,求⊙O的直径.
【分析】(1)由等腰三角形的性质和圆周角定理得出∠P=∠C,然后根据平行线的判定定理即可得到结论;
(2)连接AC,根据垂径定理及圆周角定理得到∠P=∠A,∠ACB=90°,则sinA=sinP,然后根据正弦的定义得到==,得出AB的长即可.
【解答】(1)证明:∵CM=BM,
∴∠C=∠CBM,
∵∠C=∠P,
∴∠P=∠CBM,
∴CB∥PD;
(2)解:连接AC,如图所示
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴,
∴∠BPD=∠A,
∴sinA=sin∠BPD=,
又∵AB为直径,
∴∠ACB=90°,
∴sinA==,即=,
解得:AB=,
即⊙O的直径为.
【点评】本题考查了圆的综合题:在同圆或等圆中,相等的弧所对的圆周角相等,直径所对的圆周角为直角;垂直于弦的直径平分弦,并且平分弦所对的弧;运用相似三角形的判定与性质证明线段之间的关系;运用正弦的定义进行几何计算.
19.(2015 浦东新区二模)已知:如图,在△ABC中,D是边BC上一点,以点D为圆心,CD为半径作半圆,分别与边AC、BC相交于点E和点F.如果AB=AC=5,cosB=,AE=1.求:
(1)线段CD的长度;
(2)点A和点F之间的距离.
【分析】(1)连接EF,利用圆周角定理得出∠FEC=90°,再利用等腰三角形的性质,结合锐角三角函数得出答案;
(2)利用锐角三角函数得出NC的长,再利用勾股定理得出答案.
【解答】解:(1)连接EF,
∵由题意可得FC是⊙D的直径,
∴∠FEC=90°,
∵AB=AC,
∴∠B=∠ACB,
∵AB=AC=5,cosB=,AE=1,
∴EC=4,cosB=cos∠ACB===,
解得:FC=5,
则DC=2.5;
(2)连接AF,过点A作AN⊥BC于点N,
∵AB=5,cosB=,
∴BN=4,
∴AN=3,
∵cosC=cosB=,
∴NC=4,
∴FN=1,
∴AF==.
【点评】此题主要考查了圆周角定理以及勾股定理和锐角三角函数等知识,正确应用锐角三角函数关系是解题关键.
20.(2012 肇庆)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE、AD交于点P.求证:
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)AB CE=2DP AD.
【分析】(1)由AB是⊙O的直径,可得AD⊥BC,又由AB=AC,由三线合一,即可证得D是BC的中点;
(2)由AB是⊙O的直径,∠AEB=∠ADB=90°,又由∠C是公共角,即可证得△BEC∽△ADC;
(3)易证得△ABD∽△BCE与△BPD∽△BCE,根据相似三角形的对应边成比例与BC=2BD,即可证得AB CE=2DP AD.
【解答】证明:(1)∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴D是BC的中点;
(2)∵AB是⊙O的直径,
∴∠AEB=∠ADB=90°,
即∠CEB=∠CDA=90°,
∵∠C是公共角,
∴△BEC∽△ADC;
(3)∵△BEC∽△ADC,
∴∠CBE=∠CAD,
∵AB=AC,BD=CD,
∴∠BAD=∠CAD,
∴∠BAD=∠CBE,
∵∠ADB=∠BEC=90°,
∴△ABD∽△BCE,
∴,
∴,
∵∠BDP=∠BEC=90°,∠PBD=∠CBE,
∴△BPD∽△BCE,
∴=,
∵BC=2BD,∴AB:AD=2BD:BE,
∴,
∴AB CE=2DP AD.
【点评】此题考查了相似三角形的判定与性质、圆周角定理以及等腰三角形的性质.此题难度适中,注意数形结合思想的应用.
第6页(共19页)
