26.2.2列表法与树状图法 同步练习(含答案解析)
文档属性
| 名称 | 26.2.2列表法与树状图法 同步练习(含答案解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 254.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-01 22:10:13 | ||
图片预览





文档简介
沪科版九年级数学下册26.2.2《列表法与树状图法》测试卷
一.选择题(共10小题)
1.(2016 浦东新区二模)如果从1、2、3这三个数字中任意选取两个数字,组成一个两位数,那么这个两位数是素数的概率等于( )
A.
B.
C.
D.
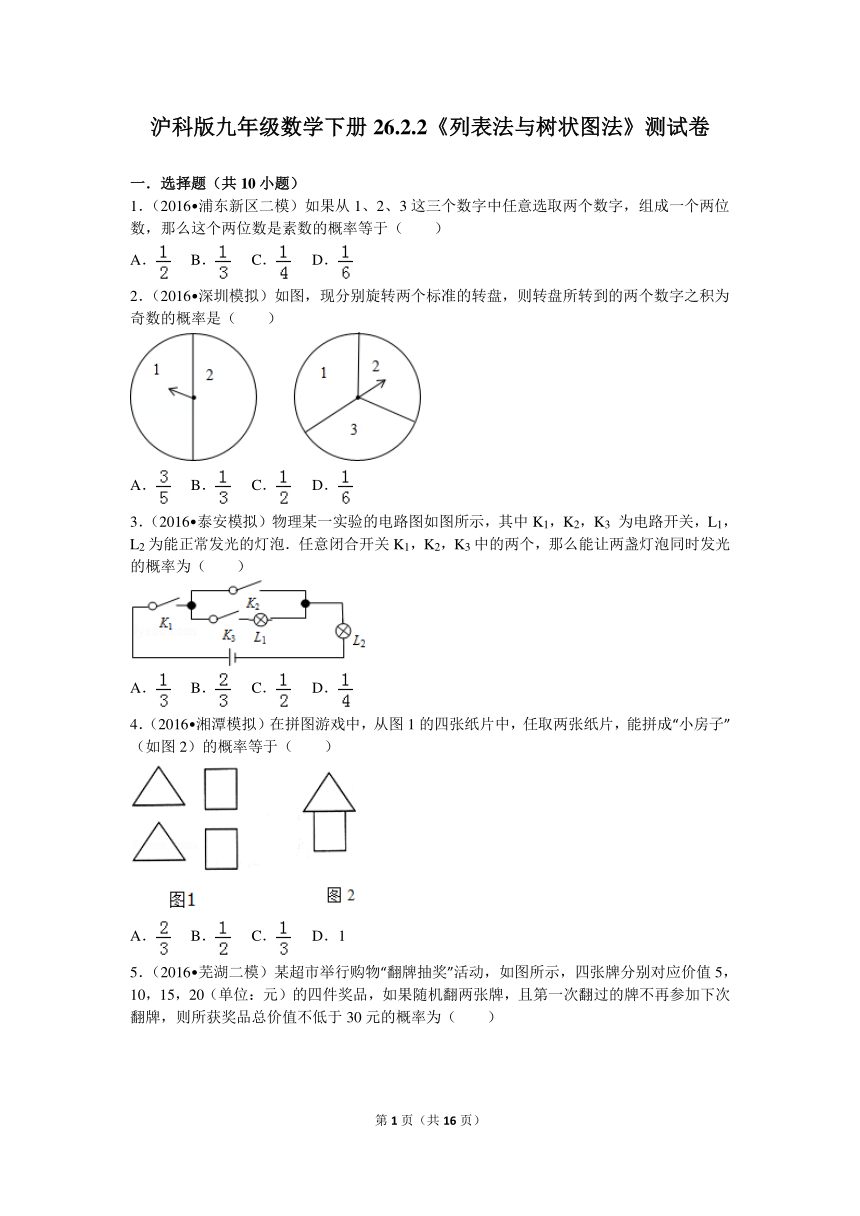
2.(2016 深圳模拟)如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是( )
A.
B.
C.
D.
3.(2016 泰安模拟)物理某一实验的电路图如图所示,其中K1,K2,K3
为电路开关,L1,L2为能正常发光的灯泡.任意闭合开关K1,K2,K3中的两个,那么能让两盏灯泡同时发光的概率为( )
A.
B.
C.
D.
4.(2016 湘潭模拟)在拼图游戏中,从图1的四张纸片中,任取两张纸片,能拼成“小房子”(如图2)的概率等于( )
A.
B.
C.
D.1
5.(2016 芜湖二模)某超市举行购物“翻牌抽奖”活动,如图所示,四张牌分别对应价值5,10,15,20(单位:元)的四件奖品,如果随机翻两张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总价值不低于30元的概率为( )
A.
B.
C.
D.
6.(2016 萧山区二模)有一箱子装有3张分别标示4,5,6的号码牌,已知小明以每次取一张且取后不放回的方式,先后取出2张牌,组成一个二位数,则组成的二位数是6的倍数的概率是( )
A.
B.
C.
D.
7.(2016 杭州校级二模)一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于n2,则算过关;否则不算过关,则能过第二关的概率是( )
A.
B.
C.
D.
8.(2016春 阜阳月考)一个骰子,六个面上的数字分别为1、2、3、4、5、6,连续投掷两次,两次向上的面出现数字之和为偶数的概率是( )
A.
B.
C.
D.
9.(2015 株洲)从2,3,4,5中任意选两个数,记作a和b,那么点(a,b)在函数y=图象上的概率是( )
A.
B.
C.
D.
10.(2015 牡丹江)学校组织校外实践活动,安排给九年级三辆车,小明与小红都可以从这三辆车中任选一辆搭乘,小明与小红同车的概率是( )
A.
B.
C.
D.
二.填空题(共4小题)
11.(2016 黄石)如图所示,一只蚂蚁从A点出发到D,E,F处寻觅食物.假定蚂蚁在每个岔路口都等可能的随机选择一条向左下或右下的路径(比如A岔路口可以向左下到达B处,也可以向右下到达C处,其中A,B,C都是岔路口).那么,蚂蚁从A出发到达E处的概率是______.
12.(2016 湘潭模拟)现有四张分别标有数字1,2,3,4的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的卡片所标数字不同的概率是______.
13.(2016 新县校级模拟)一项“过关游戏”规定:在过第n关时要将一枚质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于n2,则算过关;否则不算过关,则能过第二关的概率是______.
14.(2016 滑县一模)某商店设计了一种促销活动来吸引顾客:在一个不透明的箱子里放有4个相同的乒乓球,乒乓球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率是______.
三.解答题(共6小题)
15.(2016 昆明)甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1,2,3的小球,乙口袋中装有2个分别标有数字4,5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之和能被3整除的概率.
16.(2016 怀化)甲、乙两人都握有分别标记为A、B、C的三张牌,两人做游戏,游戏规则是:若两人出的牌不同,则A胜B,B胜C,C胜A;若两人出的牌相同,则为平局.
(1)用树状图或列表等方法,列出甲、乙两人一次游戏的所有可能的结果;
(2)求出现平局的概率.
17.(2016 淮安)如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
(1)用树状图或列表法列出所有可能出现的结果;
(2)求两个数字的积为奇数的概率.
18.(2016 临夏州)在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣的图象上的概率.
19.(2016 岳阳)已知不等式组
(1)求不等式组的解集,并写出它的所有整数解;
(2)在不等式组的所有整数解中任取两个不同的整数相乘,请用画树状图或列表的方法求积为正数的概率.
20.(2016 邵阳)为了解市民对全市创卫工作的满意程度,某中学教学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.
请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数.
(2)求此次调查中结果为非常满意的人数.
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2为进行回访,已知4为市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 浦东新区二模)如果从1、2、3这三个数字中任意选取两个数字,组成一个两位数,那么这个两位数是素数的概率等于( )
A.
B.
C.
D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与这个两位数是素数的情况,再利用概率公式求解即可求得答案.
【解答】解:画树状图得:
∵共有6种等可能的结果,这个两位数是素数的有13,23,31共3种情况,
∴这个两位数是素数的概率为:=.
故选A.
【点评】此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
2.(2016 深圳模拟)如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是( )
A.
B.
C.
D.
【分析】列表将所有等可能的结果列举出来利用概率公式求解即可.
【解答】解:列表得:
根据题意分析可得:共6种情况;为奇数的2种.
故P(奇数)==.
【点评】此题考查的是列表法与树状图法.用到的知识点为:概率=所求情况数与总情况数之比.
3.(2016 泰安模拟)物理某一实验的电路图如图所示,其中K1,K2,K3
为电路开关,L1,L2为能正常发光的灯泡.任意闭合开关K1,K2,K3中的两个,那么能让两盏灯泡同时发光的概率为( )
A.
B.
C.
D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与能让两盏灯泡同时发光的情况,再利用概率公式求解即可求得答案.
【解答】解:画树状图得:
∵共有6种等可能的结果,能让两盏灯泡同时发光的有2种情况,
∴能让两盏灯泡同时发光的概率为:P==.
故选A.
【点评】本题考查了列表法与树状图法.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比
4.(2016 湘潭模拟)在拼图游戏中,从图1的四张纸片中,任取两张纸片,能拼成“小房子”(如图2)的概率等于( )
A.
B.
C.
D.1
【分析】首先分别用A与B表示三角形与矩形,然后根据题意画树状图,由树状图求得所有等可能的结果与能拼成“小房子”(如图2)的情况,再利用概率公式求解即可求得答案,
【解答】解:分别用A与B表示三角形与矩形,
画树状图得:
∵共有12种等可能的结果,能拼成“小房子”的有8种情况,
∴任取两张纸片,能拼成“小房子”(如图2)的概率等于:=.
故选A.
【点评】此题考查了列表法或树状图法求概率.注意此题是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
5.(2016 芜湖二模)某超市举行购物“翻牌抽奖”活动,如图所示,四张牌分别对应价值5,10,15,20(单位:元)的四件奖品,如果随机翻两张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总价值不低于30元的概率为( )
A.
B.
C.
D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所获奖品总价值不低于30元的情况,再利用概率公式即可求得答案.
【解答】解:画树状图得:
∵共有12种等可能的结果,所获奖品总价值不低于30元的有4种情况,
∴所获奖品总价值不低于30元的概率为:=.
故选C.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
6.(2016 萧山区二模)有一箱子装有3张分别标示4,5,6的号码牌,已知小明以每次取一张且取后不放回的方式,先后取出2张牌,组成一个二位数,则组成的二位数是6的倍数的概率是( )
A.
B.
C.
D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与组成的二位数是6的倍数的情况,再利用概率公式即可求得答案.
【解答】解:画树状图得:
∵共有6种等可能的结果,组成的二位数是6的倍数的只有54,
∴组成的二位数是6的倍数的概率是:.
故选D.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
7.(2016 杭州校级二模)一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于n2,则算过关;否则不算过关,则能过第二关的概率是( )
A.
B.
C.
D.
【分析】利用树状展示抛掷2次的所有36种等可能的结果数,然后找出2次抛掷所出现的点数之和大于22的结果数,再根据概率公式计算出能过第二关的概率.
【解答】解:当n=2时,将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷2次,
画树状图为:
共有36种等可能的结果数,其中2次抛掷所出现的点数之和大于22的结果数为30,
所以能过第二关的概率==.
故选A.
【点评】本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.
8.(2016春 阜阳月考)一个骰子,六个面上的数字分别为1、2、3、4、5、6,连续投掷两次,两次向上的面出现数字之和为偶数的概率是( )
A.
B.
C.
D.
【分析】首先根据题意列出表格,然后由表格即可求得所有等可能的结果与两次向上的面出现数字之和为偶数的情况,再利用概率公式即可求得答案.
【解答】解:列表得:
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
∵共有36种等可能的结果,两次向上的面出现数字之和为偶数的有18种情况,
∴连续投掷两次,两次向上的面出现数字之和为偶数的概率是:=.
故选B.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
9.(2015 株洲)从2,3,4,5中任意选两个数,记作a和b,那么点(a,b)在函数y=图象上的概率是( )
A.
B.
C.
D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与点(a,b)在函数y=图象上的情况,再利用概率公式即可求得答案.
【解答】解:画树状图得:
∵共有12种等可能的结果,点(a,b)在函数y=图象上的有(3,4),(4,3);
∴点(a,b)在函数y=图象上的概率是:=.
故选D.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
10.(2015 牡丹江)学校组织校外实践活动,安排给九年级三辆车,小明与小红都可以从这三辆车中任选一辆搭乘,小明与小红同车的概率是( )
A.
B.
C.
D.
【分析】首先用A,B,C分别表示给九年级的三辆车,然后根据题意画树状图,再由树状图求得所有等可能的结果与小明与小红同车的情况,然后利用概率公式求解即可求得答案.
【解答】解:用A,B,C分别表示给九年级的三辆车,
画树状图得:
∵共有9种等可能的结果,小明与小红同车的有3种情况,
∴小明与小红同车的概率是:=.
故选C.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
二.填空题(共4小题)
11.(2016 黄石)如图所示,一只蚂蚁从A点出发到D,E,F处寻觅食物.假定蚂蚁在每个岔路口都等可能的随机选择一条向左下或右下的路径(比如A岔路口可以向左下到达B处,也可以向右下到达C处,其中A,B,C都是岔路口).那么,蚂蚁从A出发到达E处的概率是 .
【分析】首先根据题意可得共有4种等可能的结果,蚂蚁从A出发到达E处的2种情况,然后直接利用概率公式求解即可求得答案.
【解答】解:画树状图得:
∵共有4种等可能的结果,蚂蚁从A出发到达E处的2种情况,
∴蚂蚁从A出发到达E处的概率是:=.
故答案为:.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
12.(2016 湘潭模拟)现有四张分别标有数字1,2,3,4的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的卡片所标数字不同的概率是 .
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次抽出的卡片所标数字不同的情况,再利用概率公式即可求得答案.
【解答】解:画树状图得:
∵共有16种等可能的结果,两次抽出的卡片所标数字不同的有12种情况,
∴两次抽出的卡片所标数字不同的概率是:=.
故答案为:.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
13.(2016 新县校级模拟)一项“过关游戏”规定:在过第n关时要将一枚质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于n2,则算过关;否则不算过关,则能过第二关的概率是 .
【分析】由在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,n次抛掷所出现的点数之和大于n2,则算过关;可得能过第二关的抛掷所出现的点数之和需要大于5,然后根据题意列出表格,由表格求得所有等可能的结果与能过第二关的情况,再利用概率公式求解即可求得答案.
【解答】解:∵在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,n次抛掷所出现的点数之和大于n2,则算过关;
∴能过第二关的抛掷所出现的点数之和需要大于5,
列表如下:
6
7
8
9
10
11
12
5
6
7
8
9
10
11
4
5
6
7
8
9
10
3
4
5
6
7
8
9
2
3
4
5
6
7
8
1
2
3
4
5
6
7
1
2
3
4
5
6
∵共有36种等可能的结果,能过第二关的有26种情况,
∴能过第二关的概率是:=.
故答案为:.
【点评】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.
14.(2016 滑县一模)某商店设计了一种促销活动来吸引顾客:在一个不透明的箱子里放有4个相同的乒乓球,乒乓球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率是 .
【分析】首先根据题意列出表格,然后由表格即可求得所有等可能的结果与该顾客所获得购物券的金额不低于30元的情况,再利用概率公式即可求得答案.
【解答】解:列表得:
第二次第一次
0
10
20
30
0
﹣﹣
10
20
30
10
10
﹣﹣
30
40
20
20
30
﹣﹣
50
30
30
40
50
﹣﹣
∵共有12种等可能结果,该顾客所获得购物券的金额不低于30元的有8种情况,
∴P(不低于30元)==.
故答案为:.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
三.解答题(共6小题)
15.(2016 昆明)甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1,2,3的小球,乙口袋中装有2个分别标有数字4,5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之和能被3整除的概率.
【分析】先根据题意画树状图,再根据所得结果计算两个数字之和能被3整除的概率.
【解答】解:(1)树状图如下:
(2)∵共6种情况,两个数字之和能被3整除的情况数有2种,
∴两个数字之和能被3整除的概率为,
即P(两个数字之和能被3整除)=.
【点评】本题主要考查了列表法与树状图法,解决问题的关键是掌握概率的计算公式.随机事件A的概率P(A)等于事件A可能出现的结果数除以所有可能出现的结果数.
16.(2016 怀化)甲、乙两人都握有分别标记为A、B、C的三张牌,两人做游戏,游戏规则是:若两人出的牌不同,则A胜B,B胜C,C胜A;若两人出的牌相同,则为平局.
(1)用树状图或列表等方法,列出甲、乙两人一次游戏的所有可能的结果;
(2)求出现平局的概率.
【分析】(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由(1)可求得出现平局的情况,再利用概率公式求解即可求得答案.
【解答】解:(1)画树状图得:
则共有9种等可能的结果;
(2)∵出现平局的有3种情况,
∴出现平局的概率为:=.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
17.(2016 淮安)如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
(1)用树状图或列表法列出所有可能出现的结果;
(2)求两个数字的积为奇数的概率.
【分析】(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由两个数字的积为奇数的情况,再利用概率公式即可求得答案.
【解答】解:(1)画树状图得:
则共有12种等可能的结果;
(2)∵两个数字的积为奇数的4种情况,
∴两个数字的积为奇数的概率为:=.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
18.(2016 临夏州)在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣的图象上的概率.
【分析】(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由点M(x,y)在函数y=﹣的图象上的有:(1,﹣2),(2,﹣1),直接利用概率公式求解即可求得答案.
【解答】解:(1)画树状图得:
则点M所有可能的坐标为:(0,﹣1),(0,﹣2),(0,0),(1,﹣1),(1,﹣2),(1,0),(2,﹣1),(2,﹣2),(2,0);
(2)∵点M(x,y)在函数y=﹣的图象上的有:(1,﹣2),(2,﹣1),
∴点M(x,y)在函数y=﹣的图象上的概率为:.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
19.(2016 岳阳)已知不等式组
(1)求不等式组的解集,并写出它的所有整数解;
(2)在不等式组的所有整数解中任取两个不同的整数相乘,请用画树状图或列表的方法求积为正数的概率.
【分析】(1)首先分别解不等式①②,然后求得不等式组的解集,继而求得它的所有整数解;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与积为正数的情况,再利用概率公式即可求得答案.
【解答】解:(1)由①得:x>﹣2,
由②得:x≤2,
∴不等式组的解集为:﹣2<x≤2,
∴它的所有整数解为:﹣1,0,1,2;
(2)画树状图得:
∵共有12种等可能的结果,积为正数的有2种情况,
∴积为正数的概率为:=.
【点评】此题考查了列表法或树状图法求概率以及不等式组的整数解.用到的知识点为:概率=所求情况数与总情况数之比.
20.(2016 邵阳)为了解市民对全市创卫工作的满意程度,某中学教学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.
请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数.
(2)求此次调查中结果为非常满意的人数.
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2为进行回访,已知4为市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.
【分析】(1)由满意的有20人,占40%,即可求得此次调查中接受调查的人数.
(2)由(1),即可求得此次调查中结果为非常满意的人数.
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与选择的市民均来自甲区的情况,再利用概率公式即可求得答案.
【解答】解:(1)∵满意的有20人,占40%,
∴此次调查中接受调查的人数:20÷40%=50(人);
(2)此次调查中结果为非常满意的人数为:50﹣4﹣8﹣20=18(人);
(3)画树状图得:
∵共有12种等可能的结果,选择的市民均来自甲区的有2种情况,
∴选择的市民均来自甲区的概率为:=.
【点评】此题考查了列表法或树状图法求概率以及条形与扇形统计图的知识.用到的知识点为:概率=所求情况数与总情况数之比.
第5页(共16页)
一.选择题(共10小题)
1.(2016 浦东新区二模)如果从1、2、3这三个数字中任意选取两个数字,组成一个两位数,那么这个两位数是素数的概率等于( )
A.
B.
C.
D.
2.(2016 深圳模拟)如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是( )
A.
B.
C.
D.
3.(2016 泰安模拟)物理某一实验的电路图如图所示,其中K1,K2,K3
为电路开关,L1,L2为能正常发光的灯泡.任意闭合开关K1,K2,K3中的两个,那么能让两盏灯泡同时发光的概率为( )
A.
B.
C.
D.
4.(2016 湘潭模拟)在拼图游戏中,从图1的四张纸片中,任取两张纸片,能拼成“小房子”(如图2)的概率等于( )
A.
B.
C.
D.1
5.(2016 芜湖二模)某超市举行购物“翻牌抽奖”活动,如图所示,四张牌分别对应价值5,10,15,20(单位:元)的四件奖品,如果随机翻两张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总价值不低于30元的概率为( )
A.
B.
C.
D.
6.(2016 萧山区二模)有一箱子装有3张分别标示4,5,6的号码牌,已知小明以每次取一张且取后不放回的方式,先后取出2张牌,组成一个二位数,则组成的二位数是6的倍数的概率是( )
A.
B.
C.
D.
7.(2016 杭州校级二模)一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于n2,则算过关;否则不算过关,则能过第二关的概率是( )
A.
B.
C.
D.
8.(2016春 阜阳月考)一个骰子,六个面上的数字分别为1、2、3、4、5、6,连续投掷两次,两次向上的面出现数字之和为偶数的概率是( )
A.
B.
C.
D.
9.(2015 株洲)从2,3,4,5中任意选两个数,记作a和b,那么点(a,b)在函数y=图象上的概率是( )
A.
B.
C.
D.
10.(2015 牡丹江)学校组织校外实践活动,安排给九年级三辆车,小明与小红都可以从这三辆车中任选一辆搭乘,小明与小红同车的概率是( )
A.
B.
C.
D.
二.填空题(共4小题)
11.(2016 黄石)如图所示,一只蚂蚁从A点出发到D,E,F处寻觅食物.假定蚂蚁在每个岔路口都等可能的随机选择一条向左下或右下的路径(比如A岔路口可以向左下到达B处,也可以向右下到达C处,其中A,B,C都是岔路口).那么,蚂蚁从A出发到达E处的概率是______.
12.(2016 湘潭模拟)现有四张分别标有数字1,2,3,4的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的卡片所标数字不同的概率是______.
13.(2016 新县校级模拟)一项“过关游戏”规定:在过第n关时要将一枚质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于n2,则算过关;否则不算过关,则能过第二关的概率是______.
14.(2016 滑县一模)某商店设计了一种促销活动来吸引顾客:在一个不透明的箱子里放有4个相同的乒乓球,乒乓球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率是______.
三.解答题(共6小题)
15.(2016 昆明)甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1,2,3的小球,乙口袋中装有2个分别标有数字4,5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之和能被3整除的概率.
16.(2016 怀化)甲、乙两人都握有分别标记为A、B、C的三张牌,两人做游戏,游戏规则是:若两人出的牌不同,则A胜B,B胜C,C胜A;若两人出的牌相同,则为平局.
(1)用树状图或列表等方法,列出甲、乙两人一次游戏的所有可能的结果;
(2)求出现平局的概率.
17.(2016 淮安)如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
(1)用树状图或列表法列出所有可能出现的结果;
(2)求两个数字的积为奇数的概率.
18.(2016 临夏州)在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣的图象上的概率.
19.(2016 岳阳)已知不等式组
(1)求不等式组的解集,并写出它的所有整数解;
(2)在不等式组的所有整数解中任取两个不同的整数相乘,请用画树状图或列表的方法求积为正数的概率.
20.(2016 邵阳)为了解市民对全市创卫工作的满意程度,某中学教学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.
请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数.
(2)求此次调查中结果为非常满意的人数.
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2为进行回访,已知4为市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 浦东新区二模)如果从1、2、3这三个数字中任意选取两个数字,组成一个两位数,那么这个两位数是素数的概率等于( )
A.
B.
C.
D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与这个两位数是素数的情况,再利用概率公式求解即可求得答案.
【解答】解:画树状图得:
∵共有6种等可能的结果,这个两位数是素数的有13,23,31共3种情况,
∴这个两位数是素数的概率为:=.
故选A.
【点评】此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
2.(2016 深圳模拟)如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是( )
A.
B.
C.
D.
【分析】列表将所有等可能的结果列举出来利用概率公式求解即可.
【解答】解:列表得:
根据题意分析可得:共6种情况;为奇数的2种.
故P(奇数)==.
【点评】此题考查的是列表法与树状图法.用到的知识点为:概率=所求情况数与总情况数之比.
3.(2016 泰安模拟)物理某一实验的电路图如图所示,其中K1,K2,K3
为电路开关,L1,L2为能正常发光的灯泡.任意闭合开关K1,K2,K3中的两个,那么能让两盏灯泡同时发光的概率为( )
A.
B.
C.
D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与能让两盏灯泡同时发光的情况,再利用概率公式求解即可求得答案.
【解答】解:画树状图得:
∵共有6种等可能的结果,能让两盏灯泡同时发光的有2种情况,
∴能让两盏灯泡同时发光的概率为:P==.
故选A.
【点评】本题考查了列表法与树状图法.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比
4.(2016 湘潭模拟)在拼图游戏中,从图1的四张纸片中,任取两张纸片,能拼成“小房子”(如图2)的概率等于( )
A.
B.
C.
D.1
【分析】首先分别用A与B表示三角形与矩形,然后根据题意画树状图,由树状图求得所有等可能的结果与能拼成“小房子”(如图2)的情况,再利用概率公式求解即可求得答案,
【解答】解:分别用A与B表示三角形与矩形,
画树状图得:
∵共有12种等可能的结果,能拼成“小房子”的有8种情况,
∴任取两张纸片,能拼成“小房子”(如图2)的概率等于:=.
故选A.
【点评】此题考查了列表法或树状图法求概率.注意此题是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
5.(2016 芜湖二模)某超市举行购物“翻牌抽奖”活动,如图所示,四张牌分别对应价值5,10,15,20(单位:元)的四件奖品,如果随机翻两张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总价值不低于30元的概率为( )
A.
B.
C.
D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所获奖品总价值不低于30元的情况,再利用概率公式即可求得答案.
【解答】解:画树状图得:
∵共有12种等可能的结果,所获奖品总价值不低于30元的有4种情况,
∴所获奖品总价值不低于30元的概率为:=.
故选C.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
6.(2016 萧山区二模)有一箱子装有3张分别标示4,5,6的号码牌,已知小明以每次取一张且取后不放回的方式,先后取出2张牌,组成一个二位数,则组成的二位数是6的倍数的概率是( )
A.
B.
C.
D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与组成的二位数是6的倍数的情况,再利用概率公式即可求得答案.
【解答】解:画树状图得:
∵共有6种等可能的结果,组成的二位数是6的倍数的只有54,
∴组成的二位数是6的倍数的概率是:.
故选D.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
7.(2016 杭州校级二模)一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于n2,则算过关;否则不算过关,则能过第二关的概率是( )
A.
B.
C.
D.
【分析】利用树状展示抛掷2次的所有36种等可能的结果数,然后找出2次抛掷所出现的点数之和大于22的结果数,再根据概率公式计算出能过第二关的概率.
【解答】解:当n=2时,将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷2次,
画树状图为:
共有36种等可能的结果数,其中2次抛掷所出现的点数之和大于22的结果数为30,
所以能过第二关的概率==.
故选A.
【点评】本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.
8.(2016春 阜阳月考)一个骰子,六个面上的数字分别为1、2、3、4、5、6,连续投掷两次,两次向上的面出现数字之和为偶数的概率是( )
A.
B.
C.
D.
【分析】首先根据题意列出表格,然后由表格即可求得所有等可能的结果与两次向上的面出现数字之和为偶数的情况,再利用概率公式即可求得答案.
【解答】解:列表得:
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
∵共有36种等可能的结果,两次向上的面出现数字之和为偶数的有18种情况,
∴连续投掷两次,两次向上的面出现数字之和为偶数的概率是:=.
故选B.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
9.(2015 株洲)从2,3,4,5中任意选两个数,记作a和b,那么点(a,b)在函数y=图象上的概率是( )
A.
B.
C.
D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与点(a,b)在函数y=图象上的情况,再利用概率公式即可求得答案.
【解答】解:画树状图得:
∵共有12种等可能的结果,点(a,b)在函数y=图象上的有(3,4),(4,3);
∴点(a,b)在函数y=图象上的概率是:=.
故选D.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
10.(2015 牡丹江)学校组织校外实践活动,安排给九年级三辆车,小明与小红都可以从这三辆车中任选一辆搭乘,小明与小红同车的概率是( )
A.
B.
C.
D.
【分析】首先用A,B,C分别表示给九年级的三辆车,然后根据题意画树状图,再由树状图求得所有等可能的结果与小明与小红同车的情况,然后利用概率公式求解即可求得答案.
【解答】解:用A,B,C分别表示给九年级的三辆车,
画树状图得:
∵共有9种等可能的结果,小明与小红同车的有3种情况,
∴小明与小红同车的概率是:=.
故选C.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
二.填空题(共4小题)
11.(2016 黄石)如图所示,一只蚂蚁从A点出发到D,E,F处寻觅食物.假定蚂蚁在每个岔路口都等可能的随机选择一条向左下或右下的路径(比如A岔路口可以向左下到达B处,也可以向右下到达C处,其中A,B,C都是岔路口).那么,蚂蚁从A出发到达E处的概率是 .
【分析】首先根据题意可得共有4种等可能的结果,蚂蚁从A出发到达E处的2种情况,然后直接利用概率公式求解即可求得答案.
【解答】解:画树状图得:
∵共有4种等可能的结果,蚂蚁从A出发到达E处的2种情况,
∴蚂蚁从A出发到达E处的概率是:=.
故答案为:.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
12.(2016 湘潭模拟)现有四张分别标有数字1,2,3,4的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的卡片所标数字不同的概率是 .
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次抽出的卡片所标数字不同的情况,再利用概率公式即可求得答案.
【解答】解:画树状图得:
∵共有16种等可能的结果,两次抽出的卡片所标数字不同的有12种情况,
∴两次抽出的卡片所标数字不同的概率是:=.
故答案为:.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
13.(2016 新县校级模拟)一项“过关游戏”规定:在过第n关时要将一枚质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于n2,则算过关;否则不算过关,则能过第二关的概率是 .
【分析】由在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,n次抛掷所出现的点数之和大于n2,则算过关;可得能过第二关的抛掷所出现的点数之和需要大于5,然后根据题意列出表格,由表格求得所有等可能的结果与能过第二关的情况,再利用概率公式求解即可求得答案.
【解答】解:∵在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,n次抛掷所出现的点数之和大于n2,则算过关;
∴能过第二关的抛掷所出现的点数之和需要大于5,
列表如下:
6
7
8
9
10
11
12
5
6
7
8
9
10
11
4
5
6
7
8
9
10
3
4
5
6
7
8
9
2
3
4
5
6
7
8
1
2
3
4
5
6
7
1
2
3
4
5
6
∵共有36种等可能的结果,能过第二关的有26种情况,
∴能过第二关的概率是:=.
故答案为:.
【点评】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.
14.(2016 滑县一模)某商店设计了一种促销活动来吸引顾客:在一个不透明的箱子里放有4个相同的乒乓球,乒乓球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率是 .
【分析】首先根据题意列出表格,然后由表格即可求得所有等可能的结果与该顾客所获得购物券的金额不低于30元的情况,再利用概率公式即可求得答案.
【解答】解:列表得:
第二次第一次
0
10
20
30
0
﹣﹣
10
20
30
10
10
﹣﹣
30
40
20
20
30
﹣﹣
50
30
30
40
50
﹣﹣
∵共有12种等可能结果,该顾客所获得购物券的金额不低于30元的有8种情况,
∴P(不低于30元)==.
故答案为:.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
三.解答题(共6小题)
15.(2016 昆明)甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1,2,3的小球,乙口袋中装有2个分别标有数字4,5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之和能被3整除的概率.
【分析】先根据题意画树状图,再根据所得结果计算两个数字之和能被3整除的概率.
【解答】解:(1)树状图如下:
(2)∵共6种情况,两个数字之和能被3整除的情况数有2种,
∴两个数字之和能被3整除的概率为,
即P(两个数字之和能被3整除)=.
【点评】本题主要考查了列表法与树状图法,解决问题的关键是掌握概率的计算公式.随机事件A的概率P(A)等于事件A可能出现的结果数除以所有可能出现的结果数.
16.(2016 怀化)甲、乙两人都握有分别标记为A、B、C的三张牌,两人做游戏,游戏规则是:若两人出的牌不同,则A胜B,B胜C,C胜A;若两人出的牌相同,则为平局.
(1)用树状图或列表等方法,列出甲、乙两人一次游戏的所有可能的结果;
(2)求出现平局的概率.
【分析】(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由(1)可求得出现平局的情况,再利用概率公式求解即可求得答案.
【解答】解:(1)画树状图得:
则共有9种等可能的结果;
(2)∵出现平局的有3种情况,
∴出现平局的概率为:=.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
17.(2016 淮安)如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
(1)用树状图或列表法列出所有可能出现的结果;
(2)求两个数字的积为奇数的概率.
【分析】(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由两个数字的积为奇数的情况,再利用概率公式即可求得答案.
【解答】解:(1)画树状图得:
则共有12种等可能的结果;
(2)∵两个数字的积为奇数的4种情况,
∴两个数字的积为奇数的概率为:=.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
18.(2016 临夏州)在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣的图象上的概率.
【分析】(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由点M(x,y)在函数y=﹣的图象上的有:(1,﹣2),(2,﹣1),直接利用概率公式求解即可求得答案.
【解答】解:(1)画树状图得:
则点M所有可能的坐标为:(0,﹣1),(0,﹣2),(0,0),(1,﹣1),(1,﹣2),(1,0),(2,﹣1),(2,﹣2),(2,0);
(2)∵点M(x,y)在函数y=﹣的图象上的有:(1,﹣2),(2,﹣1),
∴点M(x,y)在函数y=﹣的图象上的概率为:.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
19.(2016 岳阳)已知不等式组
(1)求不等式组的解集,并写出它的所有整数解;
(2)在不等式组的所有整数解中任取两个不同的整数相乘,请用画树状图或列表的方法求积为正数的概率.
【分析】(1)首先分别解不等式①②,然后求得不等式组的解集,继而求得它的所有整数解;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与积为正数的情况,再利用概率公式即可求得答案.
【解答】解:(1)由①得:x>﹣2,
由②得:x≤2,
∴不等式组的解集为:﹣2<x≤2,
∴它的所有整数解为:﹣1,0,1,2;
(2)画树状图得:
∵共有12种等可能的结果,积为正数的有2种情况,
∴积为正数的概率为:=.
【点评】此题考查了列表法或树状图法求概率以及不等式组的整数解.用到的知识点为:概率=所求情况数与总情况数之比.
20.(2016 邵阳)为了解市民对全市创卫工作的满意程度,某中学教学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.
请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数.
(2)求此次调查中结果为非常满意的人数.
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2为进行回访,已知4为市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.
【分析】(1)由满意的有20人,占40%,即可求得此次调查中接受调查的人数.
(2)由(1),即可求得此次调查中结果为非常满意的人数.
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与选择的市民均来自甲区的情况,再利用概率公式即可求得答案.
【解答】解:(1)∵满意的有20人,占40%,
∴此次调查中接受调查的人数:20÷40%=50(人);
(2)此次调查中结果为非常满意的人数为:50﹣4﹣8﹣20=18(人);
(3)画树状图得:
∵共有12种等可能的结果,选择的市民均来自甲区的有2种情况,
∴选择的市民均来自甲区的概率为:=.
【点评】此题考查了列表法或树状图法求概率以及条形与扇形统计图的知识.用到的知识点为:概率=所求情况数与总情况数之比.
第5页(共16页)
