新疆奎屯市第一高级中学人教版高一数学必修三课件:3.2古典概型 (共27张PPT)
文档属性
| 名称 | 新疆奎屯市第一高级中学人教版高一数学必修三课件:3.2古典概型 (共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-03 12:10:25 | ||
图片预览







文档简介
课件27张PPT。3.2.1古典概型 储蓄卡密码问题问1:储蓄卡的密码一般由6个数字组成,每个数字可以是0,1,……,9十个数字中的任意一个。假设一个人完全忘记了自己的储蓄卡密码,问他在自动提款机上随机试一次密码就能取到钱的概率是多少?
同学们知道答案吗?能组织试验得出答案吗?
中奖问题
问2:某彩民随机的买一注双色球彩票,中一等奖的概率是多少?
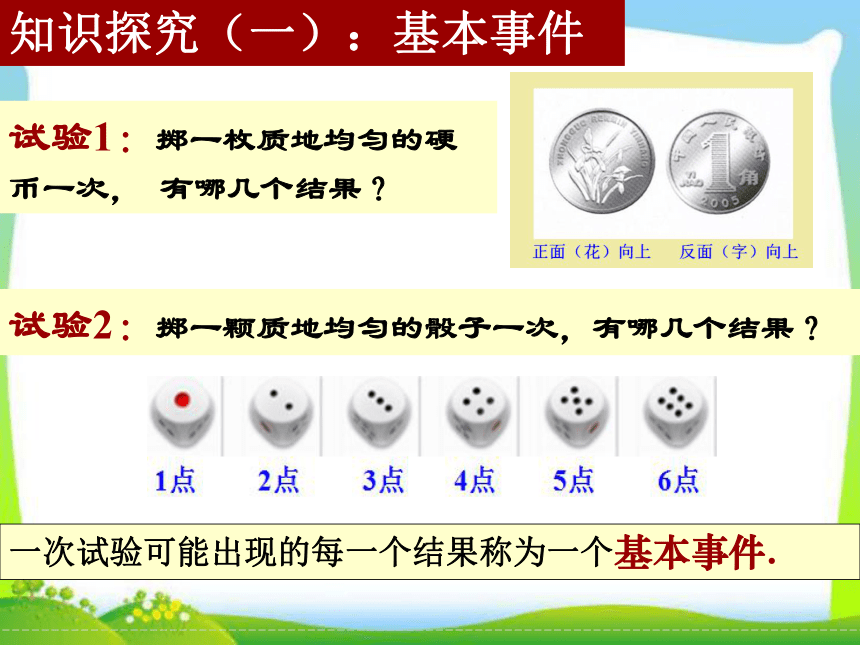
同学们知道答案吗?能组织试验得出答案吗? 通过试验和观察的方法,我们可以得到一些事件的概率估计,但这种方法耗时多,操作不方便,并且有些事件是难以组织试验的。因此,我们希望在某些特殊条件下,有一个计算事件概率的通用方法。古典概型试验1:掷一枚质地均匀的硬币一次, 有哪几个结果?试验2:掷一颗质地均匀的骰子一次,有哪几个结果?知识探究(一):基本事件 一次试验可能出现的每一个结果称为一个基本事件.(1)任何两个基本事件是互斥的。(2)任何事件(除不可能事件)都可以表示成基本事件的和。(2)事件“出现偶数点”包含哪几个基本事件?在掷一颗质地均匀的骰子一次的实验中(1)会同时出现 “1点” 与 “2点”这两个基本事件吗?基本事件的特点【做一做1】抛掷一枚骰子,下列不是基本事件的是( )
A.向上的点数是奇数 B.向上的点数是 3
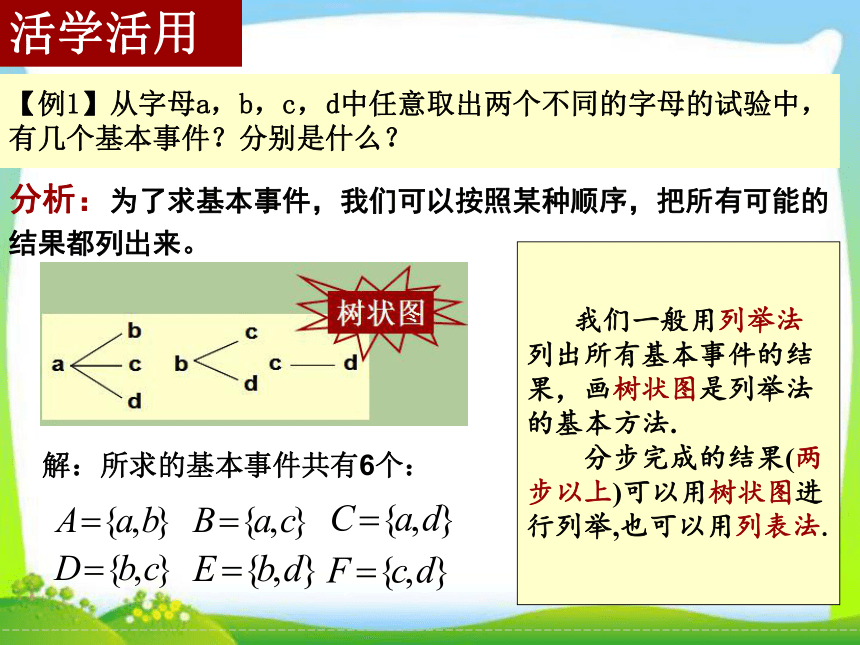
C.向上的点数是 4 D.向上的点数是 6 A活学活用【例1】从字母a,b,c,d中任意取出两个不同的字母的试验中,有几个基本事件?分别是什么?分析:为了求基本事件,我们可以按照某种顺序,把所有可能的结果都列出来。 我们一般用列举法
列出所有基本事件的结
果,画树状图是列举法
的基本方法.
分步完成的结果(两
步以上)可以用树状图进
行列举,也可以用列表法.活学活用(1) 所有可能出现的基本事件只有有限个;(有限性)
(2)每个基本事件出现的可能性相等。(等可能性) 你能从上面的两个试验和例题1发现它们的共同特点吗?思考想一想:如何判断是否为古典概型?需抓住几点?两点:有限性且等可能性。
知识探究(二):古典概型 我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型。
【做一做2】下列试验中是古典概型的是 ( ).
A.在适宜的条件下,种下一粒种子,观察它是否发芽
B.口袋里有2个白球和2个黑球,这4个球除颜色外完全
相同,从中任取一球
C.向一个圆面内随机地投一个点,该点落在圆内任意一
点都是等可能的
D.射击运动员向一靶心进行射击,试验结果为命中10
环,命中9环,…,命中0环.B判断古典概型试验1:掷一枚质地均匀的硬币一次, 有哪几个结果?试验2:掷一颗质地均匀的骰子一次,有哪几个结果?基本事件的概率古典概型每个基本事件的概率=1/n(基本事件的总数)基本事件的概率试验3:同时掷两枚质地均匀的硬币一次, 有哪几个结果?若关注结果为几个正面几个反面,则所求的基本事件共有3个:
{正,正},{正,反},{反,反}.非古典概型 若关注结果为哪个正面哪个反面,将两枚硬币标号区别,则所求的基本事件共有4个:
(正,正),(正, 反),(反,正),(反, 反).古典概型 不标号:不等可能标号:等可能将三枚硬币标号区别,所有基本事件共有8个:(正,正,正),(正,正,反),(正,反,正)(反,正,正),
(正,反,反),(反,正,反)(反,反,正),
(反,反,反).标号:等可能基本事件的概率试验4:同时掷三枚质地均匀的硬币一次, 有哪几个结果?古典概型每个基本事件的概率=1/n(基本事件的总数)【做一做3】袋中有除颜色外其他均相同的2个红球和2个黑球,从中摸出2个球,有哪几个结果?
活学活用解:设2个红球的编号为1,2,而2个黑球的编号为3,4.从袋中的4个小球中任取2个球的取法有{1,2},{1,3},{1,4},{2,3},{2,4}, {3,4} 共6种.
掷一颗均匀的骰子,事件A为“出现偶数点”,请问事件 A的概率是多少?“出现偶数点”包含 3 个基本事件:(2点,4点,6点)基本事件的总数为:6 (1点,2点,3点,4点,5点,6点)利用概率的加法公式,有:
P(A)=P(“2点”)+P(“4点”)+P(“6点”)= 1/6+1/6+1/6 = 3/6 =1/2在古典概率模型中,随机事件出现的概率又如何计算?思考 在古典概型中,如果某试验包含的所有可能结果基本事件的总数为n,随机事件A 包含基本事件的个数为m ,那么求随机事件A 的概率公式为:古典概型概率公式(1)要判断该概率模型是不是古典概型;
(2)要找出随机事件A包含的基本事件的个数和试验中基本事件的总数。3、利用公式P(A)=m/n古典概型的解题步骤是什么?想一想注:有序地写出所有基本事件及某一事件A中所包含的基本事件是解题的关键!2、求出事件A包含的基本事件个数m.“恰有两枚正面向上”包含以下3个基本事件:(正,正,反),(正,反,正),(反,正,正).【做一做4】从同时抛掷三枚质地均匀的硬币一次的试验中,记A={恰有两枚正面向上}这一事件,求P(A).
规范解题步骤解:将三枚硬币标号区别,所有基本事件共有8个:
(正,正,正),(正,正,反),(正,反,正)
(反,正,正),(正,反,反),(反,正,反)
(反,反,正),(反,反,反).单选题是标准化考试中常用的题型,一般是从A、B、C、D四个选项中选择一个正确答案.如果考生掌握了考察的内容,它可以选择唯一正确的答案.【例2】解:这是一个古典概型,因为试验的可能结果只有4个:选择A、选择B、选择C、选择D,即基本事件只有4个,考生随机的选择一个答案是选择A、B、C、D的可能性是相等的,由古典概型的概率计算公式得:假设考生不会做,他随机的选择一个答案,问他答对的概率是多少?“答对”所包含的基本事件的个数
4
=1/4=0.25
P ( “答对” )=
公式应用同时掷两个骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少? 【例3】列表法一般适用于分两步完成的结果的列举。标号公式应用解:(1)掷一个骰子的结果有6种。我们把两个标上记号1、2以便区分,由于1号骰子的每一个结果都可与2号骰子的任意一个结果配对,组成同时掷两个骰子的一个结果,因此同时掷两个骰子的结果共有36种(如图).(3)由于所有36种结果是等可能的,其中向上点数之和为5的结果(记为事件A)有4种,因此,由古典概型的概率计算公式可得(2)在上面的所有结果中,向上的点数之和为5的结果有(1,4),(2,3)(3,2)(4,1)
其中第一个数表示1号骰子的结果,第二个数表示2号骰子的结果.为什么要把两个骰子标上记号?如果不标记号会出现什么情况?你能解释其中的原因吗? 如果不标上记号,类似于(1,4)和(4,1)的结果将没有区别。 {4,1} {3,2} 思考{1,1} {2,1} {3,1} {5,1} {6,1} {2,2} {4,2} {5,2} {6,2} {3,3} {4,3} {5,3} {6,3} {4,4} {5,4} {6,4} {5,5} {6,5} {6,6} 问1:储蓄卡的密码一般由6个数字组成,每个数字可以是0,1,……,9十个数字中的任意一个。假设一个人完全忘记了自己的储蓄卡密码,问他在自动提款机上随机试一次密码就能取到钱的概率是多少?解决问题解决问题问2:某彩民随机的买一注双色球彩票,中一等奖的概率是多少?1.基本事件的定义:一次试验中可能出现的每一个结果称为一个基本事件2.基本事件的特点:(1)任何两个基本事件是互斥的
(2)任何事件(除不可能事件)都可以表示成基本事件的和3.古典概型定义及特点:(1) 所有可能出现的基本事件只有有限个(有限性)
(2)每个基本事件出现的可能性相等(等可能性)4.古典概率公式:这节课你学会了什么?判断古典概型,需抓住2点:有限性且等可能性课本P134 A组 4,5,6
B组 1,2课后作业干下去还有50%成功的希望,不干便是100%的失败。——王菊珍谢谢指导!
同学们知道答案吗?能组织试验得出答案吗?
中奖问题
问2:某彩民随机的买一注双色球彩票,中一等奖的概率是多少?
同学们知道答案吗?能组织试验得出答案吗? 通过试验和观察的方法,我们可以得到一些事件的概率估计,但这种方法耗时多,操作不方便,并且有些事件是难以组织试验的。因此,我们希望在某些特殊条件下,有一个计算事件概率的通用方法。古典概型试验1:掷一枚质地均匀的硬币一次, 有哪几个结果?试验2:掷一颗质地均匀的骰子一次,有哪几个结果?知识探究(一):基本事件 一次试验可能出现的每一个结果称为一个基本事件.(1)任何两个基本事件是互斥的。(2)任何事件(除不可能事件)都可以表示成基本事件的和。(2)事件“出现偶数点”包含哪几个基本事件?在掷一颗质地均匀的骰子一次的实验中(1)会同时出现 “1点” 与 “2点”这两个基本事件吗?基本事件的特点【做一做1】抛掷一枚骰子,下列不是基本事件的是( )
A.向上的点数是奇数 B.向上的点数是 3
C.向上的点数是 4 D.向上的点数是 6 A活学活用【例1】从字母a,b,c,d中任意取出两个不同的字母的试验中,有几个基本事件?分别是什么?分析:为了求基本事件,我们可以按照某种顺序,把所有可能的结果都列出来。 我们一般用列举法
列出所有基本事件的结
果,画树状图是列举法
的基本方法.
分步完成的结果(两
步以上)可以用树状图进
行列举,也可以用列表法.活学活用(1) 所有可能出现的基本事件只有有限个;(有限性)
(2)每个基本事件出现的可能性相等。(等可能性) 你能从上面的两个试验和例题1发现它们的共同特点吗?思考想一想:如何判断是否为古典概型?需抓住几点?两点:有限性且等可能性。
知识探究(二):古典概型 我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型。
【做一做2】下列试验中是古典概型的是 ( ).
A.在适宜的条件下,种下一粒种子,观察它是否发芽
B.口袋里有2个白球和2个黑球,这4个球除颜色外完全
相同,从中任取一球
C.向一个圆面内随机地投一个点,该点落在圆内任意一
点都是等可能的
D.射击运动员向一靶心进行射击,试验结果为命中10
环,命中9环,…,命中0环.B判断古典概型试验1:掷一枚质地均匀的硬币一次, 有哪几个结果?试验2:掷一颗质地均匀的骰子一次,有哪几个结果?基本事件的概率古典概型每个基本事件的概率=1/n(基本事件的总数)基本事件的概率试验3:同时掷两枚质地均匀的硬币一次, 有哪几个结果?若关注结果为几个正面几个反面,则所求的基本事件共有3个:
{正,正},{正,反},{反,反}.非古典概型 若关注结果为哪个正面哪个反面,将两枚硬币标号区别,则所求的基本事件共有4个:
(正,正),(正, 反),(反,正),(反, 反).古典概型 不标号:不等可能标号:等可能将三枚硬币标号区别,所有基本事件共有8个:(正,正,正),(正,正,反),(正,反,正)(反,正,正),
(正,反,反),(反,正,反)(反,反,正),
(反,反,反).标号:等可能基本事件的概率试验4:同时掷三枚质地均匀的硬币一次, 有哪几个结果?古典概型每个基本事件的概率=1/n(基本事件的总数)【做一做3】袋中有除颜色外其他均相同的2个红球和2个黑球,从中摸出2个球,有哪几个结果?
活学活用解:设2个红球的编号为1,2,而2个黑球的编号为3,4.从袋中的4个小球中任取2个球的取法有{1,2},{1,3},{1,4},{2,3},{2,4}, {3,4} 共6种.
掷一颗均匀的骰子,事件A为“出现偶数点”,请问事件 A的概率是多少?“出现偶数点”包含 3 个基本事件:(2点,4点,6点)基本事件的总数为:6 (1点,2点,3点,4点,5点,6点)利用概率的加法公式,有:
P(A)=P(“2点”)+P(“4点”)+P(“6点”)= 1/6+1/6+1/6 = 3/6 =1/2在古典概率模型中,随机事件出现的概率又如何计算?思考 在古典概型中,如果某试验包含的所有可能结果基本事件的总数为n,随机事件A 包含基本事件的个数为m ,那么求随机事件A 的概率公式为:古典概型概率公式(1)要判断该概率模型是不是古典概型;
(2)要找出随机事件A包含的基本事件的个数和试验中基本事件的总数。3、利用公式P(A)=m/n古典概型的解题步骤是什么?想一想注:有序地写出所有基本事件及某一事件A中所包含的基本事件是解题的关键!2、求出事件A包含的基本事件个数m.“恰有两枚正面向上”包含以下3个基本事件:(正,正,反),(正,反,正),(反,正,正).【做一做4】从同时抛掷三枚质地均匀的硬币一次的试验中,记A={恰有两枚正面向上}这一事件,求P(A).
规范解题步骤解:将三枚硬币标号区别,所有基本事件共有8个:
(正,正,正),(正,正,反),(正,反,正)
(反,正,正),(正,反,反),(反,正,反)
(反,反,正),(反,反,反).单选题是标准化考试中常用的题型,一般是从A、B、C、D四个选项中选择一个正确答案.如果考生掌握了考察的内容,它可以选择唯一正确的答案.【例2】解:这是一个古典概型,因为试验的可能结果只有4个:选择A、选择B、选择C、选择D,即基本事件只有4个,考生随机的选择一个答案是选择A、B、C、D的可能性是相等的,由古典概型的概率计算公式得:假设考生不会做,他随机的选择一个答案,问他答对的概率是多少?“答对”所包含的基本事件的个数
4
=1/4=0.25
P ( “答对” )=
公式应用同时掷两个骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少? 【例3】列表法一般适用于分两步完成的结果的列举。标号公式应用解:(1)掷一个骰子的结果有6种。我们把两个标上记号1、2以便区分,由于1号骰子的每一个结果都可与2号骰子的任意一个结果配对,组成同时掷两个骰子的一个结果,因此同时掷两个骰子的结果共有36种(如图).(3)由于所有36种结果是等可能的,其中向上点数之和为5的结果(记为事件A)有4种,因此,由古典概型的概率计算公式可得(2)在上面的所有结果中,向上的点数之和为5的结果有(1,4),(2,3)(3,2)(4,1)
其中第一个数表示1号骰子的结果,第二个数表示2号骰子的结果.为什么要把两个骰子标上记号?如果不标记号会出现什么情况?你能解释其中的原因吗? 如果不标上记号,类似于(1,4)和(4,1)的结果将没有区别。 {4,1} {3,2} 思考{1,1} {2,1} {3,1} {5,1} {6,1} {2,2} {4,2} {5,2} {6,2} {3,3} {4,3} {5,3} {6,3} {4,4} {5,4} {6,4} {5,5} {6,5} {6,6} 问1:储蓄卡的密码一般由6个数字组成,每个数字可以是0,1,……,9十个数字中的任意一个。假设一个人完全忘记了自己的储蓄卡密码,问他在自动提款机上随机试一次密码就能取到钱的概率是多少?解决问题解决问题问2:某彩民随机的买一注双色球彩票,中一等奖的概率是多少?1.基本事件的定义:一次试验中可能出现的每一个结果称为一个基本事件2.基本事件的特点:(1)任何两个基本事件是互斥的
(2)任何事件(除不可能事件)都可以表示成基本事件的和3.古典概型定义及特点:(1) 所有可能出现的基本事件只有有限个(有限性)
(2)每个基本事件出现的可能性相等(等可能性)4.古典概率公式:这节课你学会了什么?判断古典概型,需抓住2点:有限性且等可能性课本P134 A组 4,5,6
B组 1,2课后作业干下去还有50%成功的希望,不干便是100%的失败。——王菊珍谢谢指导!
