分类加法计数原理与分类乘法计数原理
文档属性
| 名称 | 分类加法计数原理与分类乘法计数原理 |

|
|
| 格式 | rar | ||
| 文件大小 | 705.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-16 00:00:00 | ||
图片预览







文档简介
课件28张PPT。人民教育出版社高中数学选修2—3分类加法计数原理与
分步乘法计数原理授课人: 吕廷爱
授课人单位: 山东省福山第一中学
指导教师: 刘健康
指导教师单位: 福山区教学研究培训中心选修2-3 1.1分类计数原理和分步计数原理教学目标:
认知目标: 通过实例总结出分类加法与分类乘法
计数原理,并能利用两个原理解决一些简单的
实际问题
技能情感目标:能运用两个原理解决一些问题,从
而发展学生的思维能力,培养学生分析问题和解
决问题的能力 重点:
归纳出两个原理,能运用它们解决实际问题难点:
正确区分“分类”与“分步”(一)新课导入: 汽车车牌号一般从26个英文字母、10个阿拉伯数字
中选出若干个,并按照适当顺序排列而成。随着人
们生活水平的提高,家庭汽车拥有量迅速增长。另外,
许多车主还希望自己的车牌号“个性化”,那么交通管
理部门应如何确定车号的组成方法,才能满足民众的
需求呢? 分类加法与分步乘法计数原理是计数研究中最常用、
也是最基本的两个原理。所谓计数,就是数数,把一些
对象的具体数目数出来。情况简单时可以一个一个地数,
如果数目较大时,一个一个数是不行的,利用分类加法
和分类乘法计数原理,可以帮助我们计数。 (二)新课呈现:
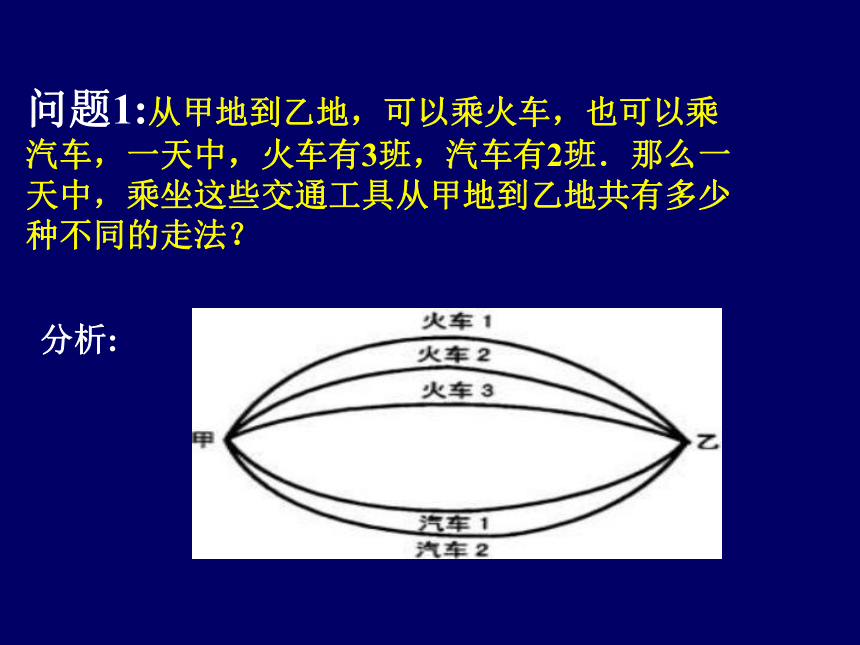
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法。那么完成这件事共有
种不同的方法分类加法计数原理: N=m+n
分类加法计数原理的推广:完成一件事有n类不同的方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,那么完成这件事共有
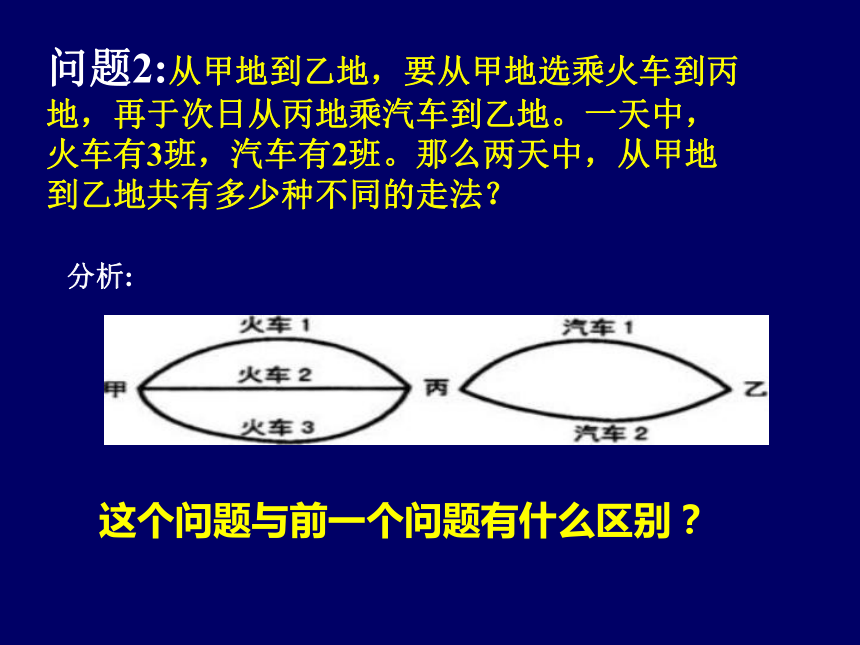
种不同的方法N=m1+m2+…+mn问题2:从甲地到乙地,要从甲地选乘火车到丙地,再于次日从丙地乘汽车到乙地。一天中,火车有3班,汽车有2班。那么两天中,从甲地到乙地共有多少种不同的走法? 分析: 这个问题与前一个问题有什么区别?
完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法。那么完成这件事共有
种不同的方法分步乘法计数原理: N=m*n 分步乘法计数原理的推广:N=m1×m2×…×mn完成一件事需要n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法。那么完成这件事共有
种不同的方法(三)典型例题:
例 3. 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书,
(1)从书架上任取1本书,有多少不同的取法?
(2)从书架的第1,2,3层各取1本书,有多少不同的取法?
分析:解题的关键是从总体上看做这件事情是“分类完成”,还是“分步完成”。“分类完成”用“分类计数原理”;“分步完成”用“分步计数原理”。
点评:
分类计数原理中的“分类”要全面, 不能遗漏; 但也不能重复、交叉;“类”与“类之间是并列的、互斥的、独立的,也就是说,完成一件事情,每次只能选择其中的一类办法中的某一种方法。
分步计数原理中的“分步”程序要正确。“步”与“步”之间是连续的,不间 断的,缺一不可;但也不能重复、交叉; 明确题目中所指的“完成一件事”是什么事,从而确定是“分类”还是“分步”㈣ 课堂练习
1 .如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
解: 按地图A、B、C、D四个区域依次分四步完成,
第一步, m1 = 3 种,
第二步, m2 = 2 种,
第三步, m3 = 1 种,
第四步, m4 = 1 种,
所以根据分步计数原理, 得到不同的涂色方案种数共有 N = 3 × 2 ×1×1 = 6 种。
2.如图,从甲地到乙地有2条路可通,从乙地到丙地有3条路可通;从甲地到丁地有4条路可通, 从丁地到丙地有2条路可通。从甲地到丙地共有多少种不同的走法?
解:从总体上看,由甲到丙有两类不同的走法,
第一类, 由甲经乙去丙,又需分两步, 所以 m1 = 2×3 = 6 种不同的走法;第二类, 由甲经丁去丙,也需分两步, 所以 m2 = 4×2 = 8 种不同的走法;所以从甲地到丙地共有 N = 6 + 8 = 14 种不同的走法。3.如图,一蚂蚁沿着长方体的棱,从它的一个顶点爬到相对的另一个顶点的最近路线共有多少条?分析:如图,从总体上看,
蚂蚁从顶点A爬到顶点C1
有三类方法,从局部上看
每类又需两步完成,所以,
第一类, m1 = 1×2 = 2 条
第二类, m2 = 1×2 = 2 条
第三类, m3 = 1×2 = 2 条
所以, 根据分类计数原理, 从顶点A到顶点C1最近路线共有 N = 2 + 2 + 2 = 6 条。
4.如图,该电路,从A到B共有多少条不同的线路可通电?
解: 从总体上看由A到B的通电线路可分三类,
第一类, m1 = 3 条
第二类, m2 = 1 条
第三类, m3 = 2×2 = 4, 条
所以, 根据分类计数原理, 从
A到B共有
N = 3 + 1 + 4 = 8
条不同的线路可通电。
当然,也可以把并联的4个看成一类,这样也可分2类求解。
(五)反馈矫正(六) 课堂小结:
1.明确题中所指的“一件事”
2.你能从自己的生活经历中举出用两个
计数原理的例子吗?(七)随堂作业根据自己的生活经验,举出一些可以用
两个计数原理计数是实际例子。谢谢指导!策 划: 张宏政
编 导: 刘兆清
刘健康
导 播: 孟广盈
摄 像: 范兆港
孙少英
制片人: 丁世俊
监 制: 解北茂福山区教育体育局
2010年4月
分步乘法计数原理授课人: 吕廷爱
授课人单位: 山东省福山第一中学
指导教师: 刘健康
指导教师单位: 福山区教学研究培训中心选修2-3 1.1分类计数原理和分步计数原理教学目标:
认知目标: 通过实例总结出分类加法与分类乘法
计数原理,并能利用两个原理解决一些简单的
实际问题
技能情感目标:能运用两个原理解决一些问题,从
而发展学生的思维能力,培养学生分析问题和解
决问题的能力 重点:
归纳出两个原理,能运用它们解决实际问题难点:
正确区分“分类”与“分步”(一)新课导入: 汽车车牌号一般从26个英文字母、10个阿拉伯数字
中选出若干个,并按照适当顺序排列而成。随着人
们生活水平的提高,家庭汽车拥有量迅速增长。另外,
许多车主还希望自己的车牌号“个性化”,那么交通管
理部门应如何确定车号的组成方法,才能满足民众的
需求呢? 分类加法与分步乘法计数原理是计数研究中最常用、
也是最基本的两个原理。所谓计数,就是数数,把一些
对象的具体数目数出来。情况简单时可以一个一个地数,
如果数目较大时,一个一个数是不行的,利用分类加法
和分类乘法计数原理,可以帮助我们计数。 (二)新课呈现:
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法。那么完成这件事共有
种不同的方法分类加法计数原理: N=m+n
分类加法计数原理的推广:完成一件事有n类不同的方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,那么完成这件事共有
种不同的方法N=m1+m2+…+mn问题2:从甲地到乙地,要从甲地选乘火车到丙地,再于次日从丙地乘汽车到乙地。一天中,火车有3班,汽车有2班。那么两天中,从甲地到乙地共有多少种不同的走法? 分析: 这个问题与前一个问题有什么区别?
完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法。那么完成这件事共有
种不同的方法分步乘法计数原理: N=m*n 分步乘法计数原理的推广:N=m1×m2×…×mn完成一件事需要n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法。那么完成这件事共有
种不同的方法(三)典型例题:
例 3. 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书,
(1)从书架上任取1本书,有多少不同的取法?
(2)从书架的第1,2,3层各取1本书,有多少不同的取法?
分析:解题的关键是从总体上看做这件事情是“分类完成”,还是“分步完成”。“分类完成”用“分类计数原理”;“分步完成”用“分步计数原理”。
点评:
分类计数原理中的“分类”要全面, 不能遗漏; 但也不能重复、交叉;“类”与“类之间是并列的、互斥的、独立的,也就是说,完成一件事情,每次只能选择其中的一类办法中的某一种方法。
分步计数原理中的“分步”程序要正确。“步”与“步”之间是连续的,不间 断的,缺一不可;但也不能重复、交叉; 明确题目中所指的“完成一件事”是什么事,从而确定是“分类”还是“分步”㈣ 课堂练习
1 .如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
解: 按地图A、B、C、D四个区域依次分四步完成,
第一步, m1 = 3 种,
第二步, m2 = 2 种,
第三步, m3 = 1 种,
第四步, m4 = 1 种,
所以根据分步计数原理, 得到不同的涂色方案种数共有 N = 3 × 2 ×1×1 = 6 种。
2.如图,从甲地到乙地有2条路可通,从乙地到丙地有3条路可通;从甲地到丁地有4条路可通, 从丁地到丙地有2条路可通。从甲地到丙地共有多少种不同的走法?
解:从总体上看,由甲到丙有两类不同的走法,
第一类, 由甲经乙去丙,又需分两步, 所以 m1 = 2×3 = 6 种不同的走法;第二类, 由甲经丁去丙,也需分两步, 所以 m2 = 4×2 = 8 种不同的走法;所以从甲地到丙地共有 N = 6 + 8 = 14 种不同的走法。3.如图,一蚂蚁沿着长方体的棱,从它的一个顶点爬到相对的另一个顶点的最近路线共有多少条?分析:如图,从总体上看,
蚂蚁从顶点A爬到顶点C1
有三类方法,从局部上看
每类又需两步完成,所以,
第一类, m1 = 1×2 = 2 条
第二类, m2 = 1×2 = 2 条
第三类, m3 = 1×2 = 2 条
所以, 根据分类计数原理, 从顶点A到顶点C1最近路线共有 N = 2 + 2 + 2 = 6 条。
4.如图,该电路,从A到B共有多少条不同的线路可通电?
解: 从总体上看由A到B的通电线路可分三类,
第一类, m1 = 3 条
第二类, m2 = 1 条
第三类, m3 = 2×2 = 4, 条
所以, 根据分类计数原理, 从
A到B共有
N = 3 + 1 + 4 = 8
条不同的线路可通电。
当然,也可以把并联的4个看成一类,这样也可分2类求解。
(五)反馈矫正(六) 课堂小结:
1.明确题中所指的“一件事”
2.你能从自己的生活经历中举出用两个
计数原理的例子吗?(七)随堂作业根据自己的生活经验,举出一些可以用
两个计数原理计数是实际例子。谢谢指导!策 划: 张宏政
编 导: 刘兆清
刘健康
导 播: 孟广盈
摄 像: 范兆港
孙少英
制片人: 丁世俊
监 制: 解北茂福山区教育体育局
2010年4月
