北师大数学七年级上2.9有理数的乘方课件
文档属性
| 名称 | 北师大数学七年级上2.9有理数的乘方课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 196.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-02 00:00:00 | ||
图片预览






文档简介
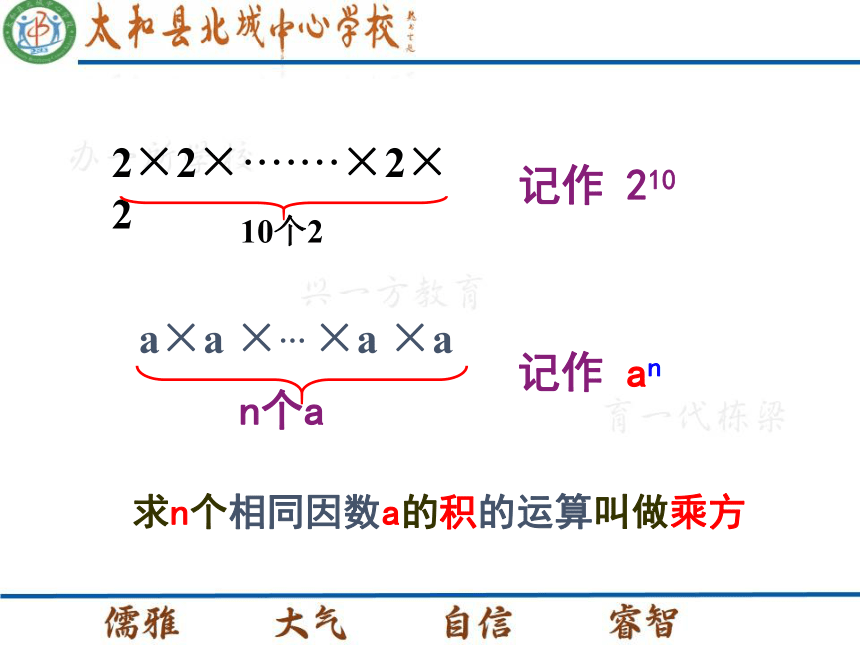
课件17张PPT。2.9 有理数的乘方学习目标1.知识目标:在现实背景中理解有理数乘方的意义,能进行有理数乘方的运算;2.能力目标:培养学生的观察、比较、分析、归纳、概括能力,以及学生的合作探索精神;3.情感态度:通过实验初步感受当底数大于1时,乘方运算的结果增长的很快,渗透分类讨论思想。1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?22×22×2×2=1024记作 210求n个相同因数a的积的运算叫做乘方记作 an2×2×·······×2×210个2指数底数幂说出下列各式的底数、指数、及其意义
(1) 53 (2) 4 2
说一说(3)((5)(-3)4 (6)-34(4)相同吗?议一议=-81 读作 的相反数,而 读作-3的 四次方 所以注意: (1)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.这也是辨认底数的方法; (2)分数的乘方,在书写时一定要把整个分数用小括号括起来.
(1) 53
(2) 4 2
(3) (-3)4
(4)
(5)
= =-=125=16=81乘方运算的符号法则:正数的任何次幂都是正数负数的偶次幂是正数, 负数的奇次幂是负数
(6)(-2)2=4(7) (-2)5=-32计算
(1) 102
103
104
(2)(-10)2
(-10)3
(-10)4 10的几次幂,1的后面就有几个0。
(-4)2底数是______指数是______(-4)2=_______
34表示___个___ 相乘(-2)3=______-8(+1)2003 -(- 1)2002=___0- 14+1=______03或-3______的平方等于91、2、3、4、5、6、棋盘上的数学 古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“陛下,就在这个棋盘上放一些米粒吧!第1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒…,一直到第64格。”“你真傻!就要这么一点米粒?!”国王哈哈大笑,大臣说:“就怕您的国库里没有这么多米!”第1格: 1第2格:第3格:2第4格: 第5格:……第64格:4=2 ×28= 2 ×2 ×263个2?=2×2×······×2聪明的同学们,你认为国王的国库里有这么多米吗?按照这个大臣的要求,只棋盘上的第64格就需要263粒米。这个数是9223372036854775808.如果一斤米大约为10000粒,则大约为922万亿斤,而作为农业大国,我国2004年一年的粮食产量大约为9389亿斤1. 乘方:求n个相同因数a的积的运算叫做乘方.an读作a的n次幂(或a的n次方)。 a·a·…·a= n个 an(1)幂的意义:表示几个相同因数a相乘
(2)注意两种幂的写法:①底数是负数的幂,如
②底数是分数的幂,如这节课你收获了什么?2.正数的任何次幂都是正数;
负数的奇次幂是负数,
负数的偶次幂是正数珠穆朗玛峰是世界的最高峰,它的海拔高度是8848米。
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰。这是真的吗?≈ ≈
(1) 53 (2) 4 2
说一说(3)((5)(-3)4 (6)-34(4)相同吗?议一议=-81 读作 的相反数,而 读作-3的 四次方 所以注意: (1)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.这也是辨认底数的方法; (2)分数的乘方,在书写时一定要把整个分数用小括号括起来.
(1) 53
(2) 4 2
(3) (-3)4
(4)
(5)
= =-=125=16=81乘方运算的符号法则:正数的任何次幂都是正数负数的偶次幂是正数, 负数的奇次幂是负数
(6)(-2)2=4(7) (-2)5=-32计算
(1) 102
103
104
(2)(-10)2
(-10)3
(-10)4 10的几次幂,1的后面就有几个0。
(-4)2底数是______指数是______(-4)2=_______
34表示___个___ 相乘(-2)3=______-8(+1)2003 -(- 1)2002=___0- 14+1=______03或-3______的平方等于91、2、3、4、5、6、棋盘上的数学 古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“陛下,就在这个棋盘上放一些米粒吧!第1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒…,一直到第64格。”“你真傻!就要这么一点米粒?!”国王哈哈大笑,大臣说:“就怕您的国库里没有这么多米!”第1格: 1第2格:第3格:2第4格: 第5格:……第64格:4=2 ×28= 2 ×2 ×263个2?=2×2×······×2聪明的同学们,你认为国王的国库里有这么多米吗?按照这个大臣的要求,只棋盘上的第64格就需要263粒米。这个数是9223372036854775808.如果一斤米大约为10000粒,则大约为922万亿斤,而作为农业大国,我国2004年一年的粮食产量大约为9389亿斤1. 乘方:求n个相同因数a的积的运算叫做乘方.an读作a的n次幂(或a的n次方)。 a·a·…·a= n个 an(1)幂的意义:表示几个相同因数a相乘
(2)注意两种幂的写法:①底数是负数的幂,如
②底数是分数的幂,如这节课你收获了什么?2.正数的任何次幂都是正数;
负数的奇次幂是负数,
负数的偶次幂是正数珠穆朗玛峰是世界的最高峰,它的海拔高度是8848米。
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰。这是真的吗?≈ ≈
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
