北师大版九年级上6.3反比例函数的应用课件
文档属性
| 名称 | 北师大版九年级上6.3反比例函数的应用课件 |  | |
| 格式 | zip | ||
| 文件大小 | 281.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-02 20:38:40 | ||
图片预览









文档简介
课件30张PPT。第六章 反比例函数 6.3 反比例函数的应用2.反比例函数图象是什么?1.什么是反比例函数?是双曲线当k>0时,两支曲线分别位于第一、三象限内,在每一象限内,y随x的增大而减少;
当k<0时,两支曲线分别位于第二、四象限,在每一象限内,y随x的增大而增大.
近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则y与x之间的函数关系式为 .
若点(2,-4)在反比例函数 的图象上,则k=____.
若反比例函数 的图象在第二、四象限,
则k的取值范围是____________.
反比例函数的图象既是______对称图形,又是 ______对称图形函数 的图象上有三点(-3,y1),
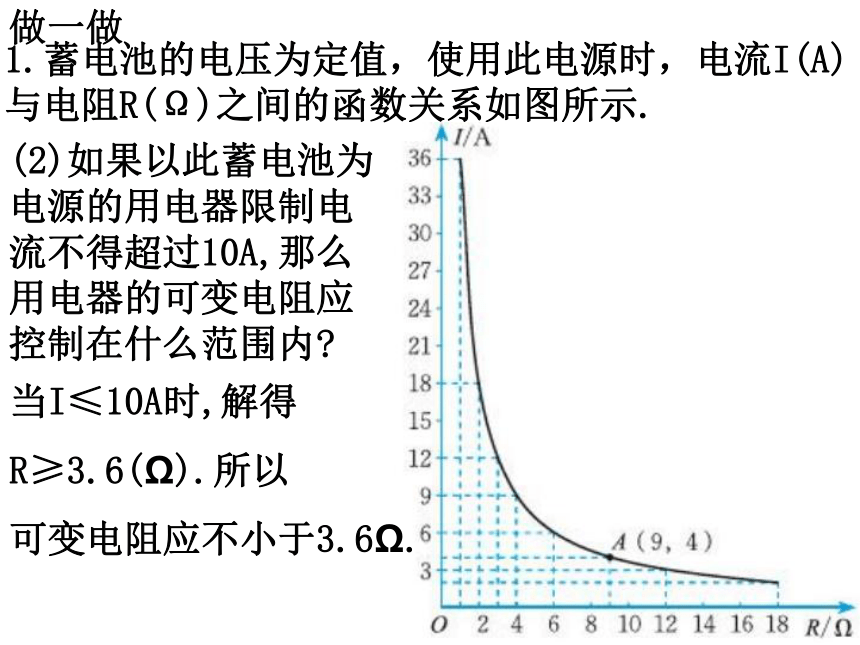
(-1,y2), (2,y3)则函数值y1、y2、y3的大小关系是_______________;K〈-1-8轴中心y3< y1< y2某科技小组进行野外考察,利用铺垫木板的方式通过了一片烂泥湿地,你能解释这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强P(Pa)将如何变化?如果人和木板对湿地地面的压力合计600N,那么(1)用含S的代数式表示P,P是S的反比例函数吗?为什么?P是S的反比例函数.如果人和木板对湿地地面的压力合计600N,那么(2)当木板面积为0.2m2时,压强是多少?(3)如果要求压强不超过6000Pa,木板面积至少要多大?所以木板面积至少要0.1m2.即S ≥0.1如果人和木板对湿地地面的压力合计600N,那么(4)在平面直角坐标系中,画出相应的函数图象。注意:只需在第一象限作出函数的图象.因为S>0.如果人和木板对湿地地面的压力合计600N,那么(5)请利用图象对(2)和(3)作出直观解释,并与同伴交流.问题(2)是已知图象上的某点的横坐标为0.2,求该点的纵坐标;问题(3)是已知图象上点的纵坐标不大于6000,求这些点所处位置及它们横坐标的取值范围.实际上这些点都在直线P=6000下方的图象上(含直线P=6000与图象的交点).做一做1.蓄电池的电压为定值,使用此电源时,电流I(A)与电阻R(Ω)之间的函数关系如图所示.(1)蓄电池的电压是多少?你能写出这一函数的表达式吗?因为电流I与电压U之间的关系为IR=U(U为定值),把图象上的点A的坐标(9,4)代入,得U=36.所以蓄电池的电压U=36V.做一做1.蓄电池的电压为定值,使用此电源时,电流I(A)与电阻R(Ω)之间的函数关系如图所示.(2)如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内?当I≤10A时,解得
R≥3.6(Ω).所以
可变电阻应不小于3.6Ω.做一做(1)分别写出这两个函数的表达式;所求的函数表达式为:
y=2x和做一做(2)你能求出点B的坐标吗?你是怎样求的?B点的坐标是两个函数组成的方程组的另一个解.做一做(3)观察图象回答:x为何值时,反比例函数值小于一次函数值?练习某蓄水池排水管的排水速度是8m3/h,6h可将满池水全部排空.蓄水池的容积为:8×6=48(m3).(2)如果增加排水管,使排水速度达到Q(m3/h),那么将满池水排空所需的时间t(h)将如何变化?此时所需时间t(h)将减少.(3)写出t与Q之间的关系式;(1)蓄水池的容积是多少?(4)如果准备在5h内将满池水排空,那么排水速度至少为多少?至少为9.6m3.(5)已知排水管的最大排水速度为12m3/h,那么最少多长时间可将满池水全部排空?最少4h。某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(KPA)是气体体积V(m3)的反比例函数,其图象如图所示.(1)写出这一函数的表达式;(2)当气体体积为1m3时,气压是多少?P=96kpa(3)当气球内的气压大于140kpa时,气球将爆炸.为了安全起见,气球的体积应不小于多少?(1)写出这两个函数的表达式,并确定这两个函数图象的另一个交点的坐标;(2)画出草图,并据此写出使反比例函数值大于正比例函数值的x的取值范围。x<-1或0<x<1.在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V 时,气体的密度ρ也随之改变.ρ与V 在一定范围内满足,它的图象如图所示,则该气体的质量m为( )
A.1.4kg B. 5kg
C.6.4kg D.7kg D如图所示,P1、P2、P3是双曲线上的三个点,过这三点分别作y轴的垂线,得三个三角形OP1A1、OP2A2、OP3A3,设它们的面积分别为S1、S2、S3,则( )
A.S1 C.S1< S3< S2 D. S1=S2=S3D如图,已知点A是一次函数y=x图象与反比例函数
的图象在第一象限内的交点,点B 在x
轴的负半轴上,且OA=OB,那么△AOB的面积为( ).
A. 2 B.
C. D. C将油箱注满k升油后,轿车科行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反
比例函数关系S= (k是常数,k≠0).已知某轿
车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(1)求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式(关系式);
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?
如图,正比例函数y=x与反比例函数 的图象交关于A、C两点,分别过A、C 作AB⊥x 轴于B,CD⊥x 轴于D,则四边形ABCD的面积为( )
A.1 B. C.2 D.C在反比例函数 的图象上有两点A(x1,
y1),B(x2,y2),且x1>x2>0,则y1-y2的值是( )
A. 正数 B. 负数
C. 非正数 D. 不能确定A如图,在直角坐标系中,O为原点,A(4,12)为双曲线上的一点.
(1)求k的值;
(2)过双曲线上的点P作PB⊥x 轴于B,连接OP,若
Rt△OPB的两直角边的比值为 ,试求点P的坐标.
如图,正方形OABC,ADEF的顶点A、D、C在坐标轴上,点F在AB上,点B、E在函数 的图象上,则点E的坐标是( )
A. B.
C.
D. A提示:B(1,1),设E纵坐标为y.
则y(y+1)=1如图,△OP1A1、△A1P2A2是等腰直角三角形,点P1、
P2在函数 的图象上,
斜边OA1、A1A2都在x轴上,则点A2的坐标是 .
提示:设P2纵坐标为y,则y(y+4)=4.小结:
学完本课后你有哪些收获?作业:
习题6.4 1、2、3题。
当k<0时,两支曲线分别位于第二、四象限,在每一象限内,y随x的增大而增大.
近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则y与x之间的函数关系式为 .
若点(2,-4)在反比例函数 的图象上,则k=____.
若反比例函数 的图象在第二、四象限,
则k的取值范围是____________.
反比例函数的图象既是______对称图形,又是 ______对称图形函数 的图象上有三点(-3,y1),
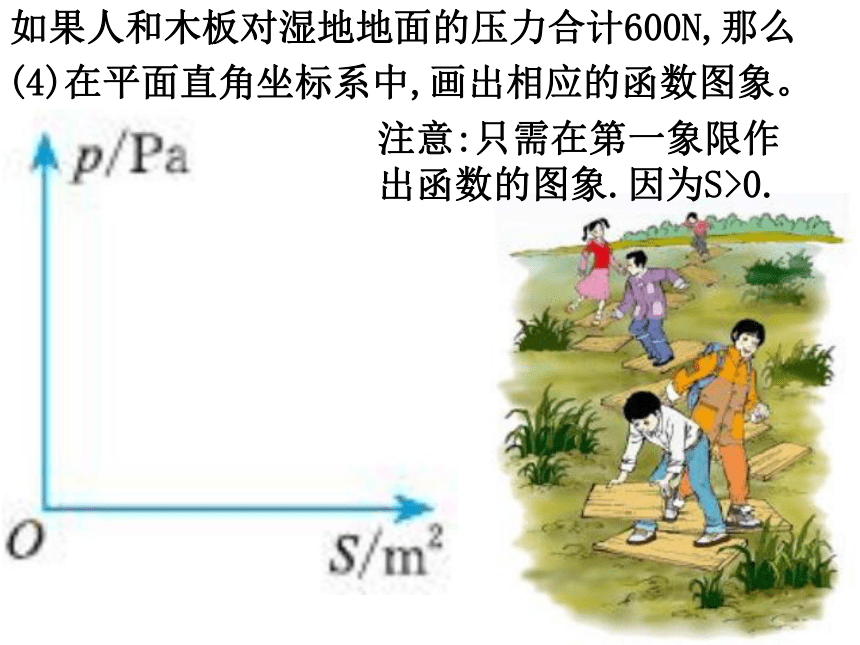
(-1,y2), (2,y3)则函数值y1、y2、y3的大小关系是_______________;K〈-1-8轴中心y3< y1< y2某科技小组进行野外考察,利用铺垫木板的方式通过了一片烂泥湿地,你能解释这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强P(Pa)将如何变化?如果人和木板对湿地地面的压力合计600N,那么(1)用含S的代数式表示P,P是S的反比例函数吗?为什么?P是S的反比例函数.如果人和木板对湿地地面的压力合计600N,那么(2)当木板面积为0.2m2时,压强是多少?(3)如果要求压强不超过6000Pa,木板面积至少要多大?所以木板面积至少要0.1m2.即S ≥0.1如果人和木板对湿地地面的压力合计600N,那么(4)在平面直角坐标系中,画出相应的函数图象。注意:只需在第一象限作出函数的图象.因为S>0.如果人和木板对湿地地面的压力合计600N,那么(5)请利用图象对(2)和(3)作出直观解释,并与同伴交流.问题(2)是已知图象上的某点的横坐标为0.2,求该点的纵坐标;问题(3)是已知图象上点的纵坐标不大于6000,求这些点所处位置及它们横坐标的取值范围.实际上这些点都在直线P=6000下方的图象上(含直线P=6000与图象的交点).做一做1.蓄电池的电压为定值,使用此电源时,电流I(A)与电阻R(Ω)之间的函数关系如图所示.(1)蓄电池的电压是多少?你能写出这一函数的表达式吗?因为电流I与电压U之间的关系为IR=U(U为定值),把图象上的点A的坐标(9,4)代入,得U=36.所以蓄电池的电压U=36V.做一做1.蓄电池的电压为定值,使用此电源时,电流I(A)与电阻R(Ω)之间的函数关系如图所示.(2)如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内?当I≤10A时,解得
R≥3.6(Ω).所以
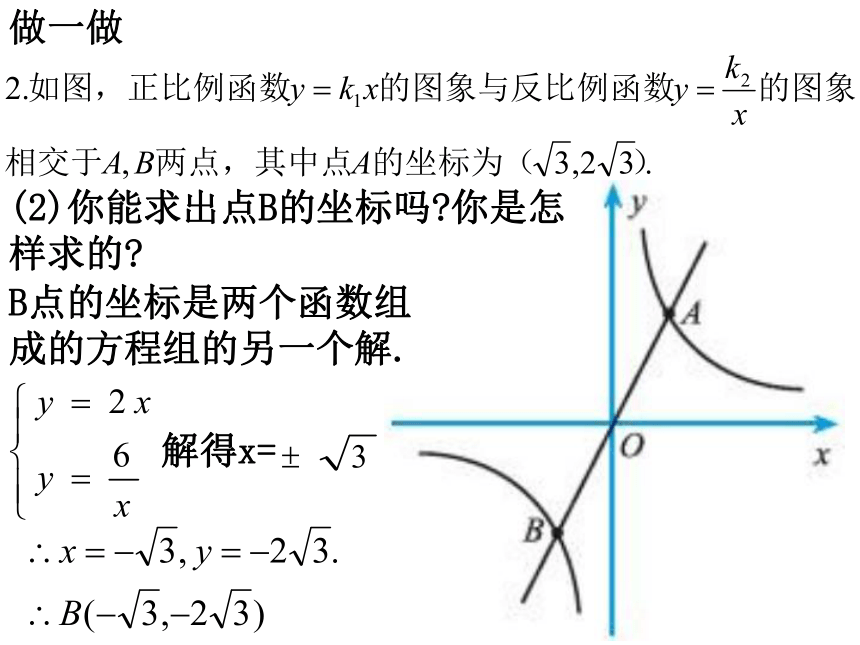
可变电阻应不小于3.6Ω.做一做(1)分别写出这两个函数的表达式;所求的函数表达式为:
y=2x和做一做(2)你能求出点B的坐标吗?你是怎样求的?B点的坐标是两个函数组成的方程组的另一个解.做一做(3)观察图象回答:x为何值时,反比例函数值小于一次函数值?练习某蓄水池排水管的排水速度是8m3/h,6h可将满池水全部排空.蓄水池的容积为:8×6=48(m3).(2)如果增加排水管,使排水速度达到Q(m3/h),那么将满池水排空所需的时间t(h)将如何变化?此时所需时间t(h)将减少.(3)写出t与Q之间的关系式;(1)蓄水池的容积是多少?(4)如果准备在5h内将满池水排空,那么排水速度至少为多少?至少为9.6m3.(5)已知排水管的最大排水速度为12m3/h,那么最少多长时间可将满池水全部排空?最少4h。某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(KPA)是气体体积V(m3)的反比例函数,其图象如图所示.(1)写出这一函数的表达式;(2)当气体体积为1m3时,气压是多少?P=96kpa(3)当气球内的气压大于140kpa时,气球将爆炸.为了安全起见,气球的体积应不小于多少?(1)写出这两个函数的表达式,并确定这两个函数图象的另一个交点的坐标;(2)画出草图,并据此写出使反比例函数值大于正比例函数值的x的取值范围。x<-1或0<x<1.在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V 时,气体的密度ρ也随之改变.ρ与V 在一定范围内满足,它的图象如图所示,则该气体的质量m为( )
A.1.4kg B. 5kg
C.6.4kg D.7kg D如图所示,P1、P2、P3是双曲线上的三个点,过这三点分别作y轴的垂线,得三个三角形OP1A1、OP2A2、OP3A3,设它们的面积分别为S1、S2、S3,则( )
A.S1
的图象在第一象限内的交点,点B 在x
轴的负半轴上,且OA=OB,那么△AOB的面积为( ).
A. 2 B.
C. D. C将油箱注满k升油后,轿车科行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反
比例函数关系S= (k是常数,k≠0).已知某轿
车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(1)求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式(关系式);
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?
如图,正比例函数y=x与反比例函数 的图象交关于A、C两点,分别过A、C 作AB⊥x 轴于B,CD⊥x 轴于D,则四边形ABCD的面积为( )
A.1 B. C.2 D.C在反比例函数 的图象上有两点A(x1,
y1),B(x2,y2),且x1>x2>0,则y1-y2的值是( )
A. 正数 B. 负数
C. 非正数 D. 不能确定A如图,在直角坐标系中,O为原点,A(4,12)为双曲线上的一点.
(1)求k的值;
(2)过双曲线上的点P作PB⊥x 轴于B,连接OP,若
Rt△OPB的两直角边的比值为 ,试求点P的坐标.
如图,正方形OABC,ADEF的顶点A、D、C在坐标轴上,点F在AB上,点B、E在函数 的图象上,则点E的坐标是( )
A. B.
C.
D. A提示:B(1,1),设E纵坐标为y.
则y(y+1)=1如图,△OP1A1、△A1P2A2是等腰直角三角形,点P1、
P2在函数 的图象上,
斜边OA1、A1A2都在x轴上,则点A2的坐标是 .
提示:设P2纵坐标为y,则y(y+4)=4.小结:
学完本课后你有哪些收获?作业:
习题6.4 1、2、3题。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
