【北师大版】数学九年级上册课件2.1认识一元二次方程第2课时
文档属性
| 名称 | 【北师大版】数学九年级上册课件2.1认识一元二次方程第2课时 |

|
|
| 格式 | zip | ||
| 文件大小 | 253.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-03 00:00:00 | ||
图片预览




文档简介
课件10张PPT。1 认识一元二次方程(二)第二章 一元二次方程花边有多宽一块四周镶有宽度相等的花边的地毯如下图,它的长为8m,宽为5m.如果地毯中央长方形图案的面积为18m2 ,则花边多宽?你怎么解决这个问题?估算一元二次方程的解解:如果设花边的宽为xm , 根据题意得你能求出x吗?怎么去估计x呢?(8 - 2x) (5 - 2x) = 18.即2x2-13x+11 = 0.你能猜得出x取值的大致范围吗?X可能小于等于0吗?说说你的理由.X可能大于等于4吗?可能大于等于2.5吗?说说你的理由.因此,x取值的大致范围是:0则有8-2x=6, 5-2x=3.从而也可以解得x=1.怎么样,你还敢挑战吗?
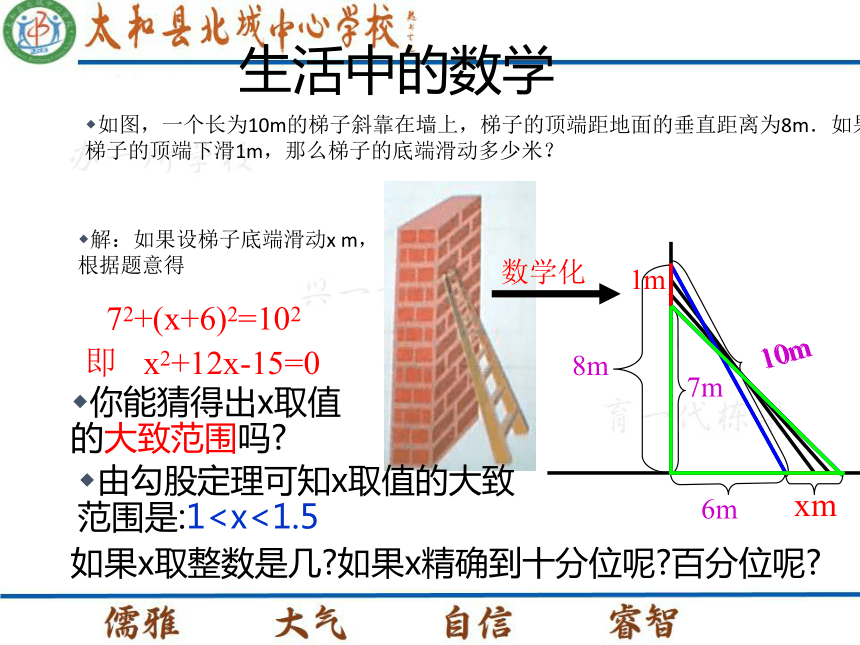
你能总结出估算的方法步骤和提高估算的能力吗? 0.5 1 1.5 2 5 0 -4 -7生活中的数学如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?解:如果设梯子底端滑动x m,根据题意得你能猜得出x取值的大致范围吗?72+(x+6)2=102即 x2+12x-15=0由勾股定理可知x取值的大致范围是:1102+112+122=132+142
你还能找到其他的五个连续整数,使前三个数的平方和等于后两个数的平方和吗?如果设五个连续整数中的第一个数为x,那么后面四个数依次可表示为: , , , .即 x2-8x-20=0.根据题意,可得方程:
.你能求出这五个整数分别是多少吗?本节课你又学会了哪些新知识呢?
学习了估算一元二次方程
ax2+bx+c=0(a,b,c为常数,a≠0)
近似解的方法;
知道了估算步骤:
先确定大致范围;
再取值计算,逐步逼近.
想一想,有没有便捷的方法去求方程中的未知数呢?小 结练 习根据题意,列出方程,并估算方程的解:1.一面积为120m2的矩形苗圃,它的长比宽多2m,苗圃的长和宽各是多少?解:设矩形的宽为xm,则长为(x+2) m, 根据题意得: x (x+2) =120.即x2 + 2x-120 =0.xx+2120m2根据题意,x的取值范围大致是0 1.2
你能总结出估算的方法步骤和提高估算的能力吗? 0.5 1 1.5 2 5 0 -4 -7生活中的数学如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?解:如果设梯子底端滑动x m,根据题意得你能猜得出x取值的大致范围吗?72+(x+6)2=102即 x2+12x-15=0由勾股定理可知x取值的大致范围是:1
你还能找到其他的五个连续整数,使前三个数的平方和等于后两个数的平方和吗?如果设五个连续整数中的第一个数为x,那么后面四个数依次可表示为: , , , .即 x2-8x-20=0.根据题意,可得方程:
.你能求出这五个整数分别是多少吗?本节课你又学会了哪些新知识呢?
学习了估算一元二次方程
ax2+bx+c=0(a,b,c为常数,a≠0)
近似解的方法;
知道了估算步骤:
先确定大致范围;
再取值计算,逐步逼近.
想一想,有没有便捷的方法去求方程中的未知数呢?小 结练 习根据题意,列出方程,并估算方程的解:1.一面积为120m2的矩形苗圃,它的长比宽多2m,苗圃的长和宽各是多少?解:设矩形的宽为xm,则长为(x+2) m, 根据题意得: x (x+2) =120.即x2 + 2x-120 =0.xx+2120m2根据题意,x的取值范围大致是0
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
