【北师大版】数学九年级上册课件2.6应用一元二次方程第2课时
文档属性
| 名称 | 【北师大版】数学九年级上册课件2.6应用一元二次方程第2课时 |

|
|
| 格式 | pptx | ||
| 文件大小 | 143.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-03 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第二章 一元二次方程
6 应用一元二次方程(二)
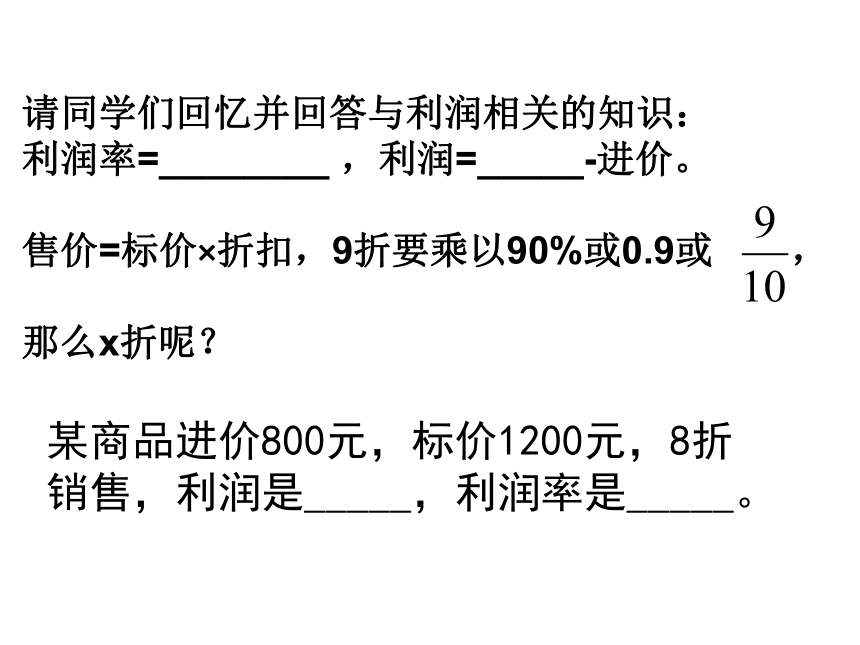
请同学们回忆并回答与利润相关的知识:
利润率=________ ,利润=_____-进价。
售价=标价×折扣,9折要乘以90%或0.9或 ,
那么x折呢?
某商品进价800元,标价1200元,8折销售,利润是_____,利润率是_____。
例:新华商场销售某种冰箱,每台进货价为2500元。调查发现,当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台。商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
如果设每台冰箱降价x元,那么每台冰箱的定价
就是————————————元,每台冰箱的销售利润
为————————————元,平均每天销售冰箱的数
量为————————————台。这样就可以列出一个方程,从而使问题得到解决。
分析:本题的主要等量关系:
每台冰箱的销售利润×平均每天销售冰箱的数量=5000元
(2900-x-2500)
(2900-x)
也可以用列表的方法进行分析:(如下表)
每天的销售量/台 每台的销售利润/元 总销售利润/元
降价前
降价后
8
2900-2500
(2900-2500)×8
2900-x-2500
5000
思考:本题若设定价为x元,应怎么列方程
做一做
某商场将进货价为30元的台灯以40元售出,平均每月能售出600个。调查发现,售价在40元至60元范围内,这种台灯的售价每上涨1元,其销售量就将减少10个。为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少?这时应进台灯多少个?
50元,500个
议一议
利用方程解决实际问题的关键是什么?
寻找等量关系
练习
某批发市场礼品柜台春节期间购进大量贺年片,一种贺年片平均每天能售出500张,每张盈利0.3元.为了尽快减少库存,摊主决定采取适当的降价措施.调查发现,如果这种贺年卡的售价每降价0.05元,那么平均每天可多售出200张.摊主要想平均每天盈利180元,每张贺年片应降价多少元
某种服装,平均每天可销售20件,每件盈利44元.在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售5件.如果每天盈利1600元,每件应降价多少元
(不合题意,舍去)
答:每件服装应降价4元.
一个班每两个人都互相握手一次,有人统计一共握了3003次手,请问这班的人数是多少?
某农场2012年粮食产量800万千克,2014年为930万千克,如果年平均增长率为,则列出方程为________
某单位为节省经费,在两个月内将开支从每月1600元降到900元,求这个单位平均每月降低的百分率是多少
某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株
(x+3)(3-0.5x)=10
解这个方程,得:x1=1, x2=2
答:要使每盆的盈利达到10元,每盆应植入4株或5株.
一个农业合作社以64000元的成本收获了某种农场品80t,目前可以以1200元/t的价格出售。如果储藏起来,每星期会损失2t,且每星期需支付各种费用1600元,但同时每星期每吨的价格将上涨200元。那么,储藏多少个星期出售这批农场品可获利122000元?
解:设储藏x个星期出售这批农场品可获利122000元,根据题意,得
(80-2x)(1200+200x)-1600x-64000=122000
整理,得 x2-30x+225=0
解得 x1=x2=15
所以,储藏15个星期出售这批农场品可获利122000元。
某公司今年10月的营业额为2500万元,按计划第四季度的总营业额要达到9100万元,求该公司11,12两个月营业额的月均增长率。
解:设该公司11,12两个月营业额的月均增长率为x,根据题意,得
2500+2500(1+x)+2500(1+x)2=9100
整理,得 x2+3x-0.64=0
解得 x1=0.2,x2=-3.2(不合题意,舍去)
所以,设该公司11,12两个月营业额的月均增长率为20%。
列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么 已知,未知之间有什么关系
2.设:设未知数,语句要完整,有单位(统一)的要注明单位;
3.列:列代数式,列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:答案也必须是完整的语句,注明单位且要贴近生活.
列方程解应用题的关键是:
寻找等量关系
作业:
习题2.10 1、2、3、4题。
第二章 一元二次方程
6 应用一元二次方程(二)
请同学们回忆并回答与利润相关的知识:
利润率=________ ,利润=_____-进价。
售价=标价×折扣,9折要乘以90%或0.9或 ,
那么x折呢?
某商品进价800元,标价1200元,8折销售,利润是_____,利润率是_____。
例:新华商场销售某种冰箱,每台进货价为2500元。调查发现,当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台。商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
如果设每台冰箱降价x元,那么每台冰箱的定价
就是————————————元,每台冰箱的销售利润
为————————————元,平均每天销售冰箱的数
量为————————————台。这样就可以列出一个方程,从而使问题得到解决。
分析:本题的主要等量关系:
每台冰箱的销售利润×平均每天销售冰箱的数量=5000元
(2900-x-2500)
(2900-x)
也可以用列表的方法进行分析:(如下表)
每天的销售量/台 每台的销售利润/元 总销售利润/元
降价前
降价后
8
2900-2500
(2900-2500)×8
2900-x-2500
5000
思考:本题若设定价为x元,应怎么列方程
做一做
某商场将进货价为30元的台灯以40元售出,平均每月能售出600个。调查发现,售价在40元至60元范围内,这种台灯的售价每上涨1元,其销售量就将减少10个。为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少?这时应进台灯多少个?
50元,500个
议一议
利用方程解决实际问题的关键是什么?
寻找等量关系
练习
某批发市场礼品柜台春节期间购进大量贺年片,一种贺年片平均每天能售出500张,每张盈利0.3元.为了尽快减少库存,摊主决定采取适当的降价措施.调查发现,如果这种贺年卡的售价每降价0.05元,那么平均每天可多售出200张.摊主要想平均每天盈利180元,每张贺年片应降价多少元
某种服装,平均每天可销售20件,每件盈利44元.在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售5件.如果每天盈利1600元,每件应降价多少元
(不合题意,舍去)
答:每件服装应降价4元.
一个班每两个人都互相握手一次,有人统计一共握了3003次手,请问这班的人数是多少?
某农场2012年粮食产量800万千克,2014年为930万千克,如果年平均增长率为,则列出方程为________
某单位为节省经费,在两个月内将开支从每月1600元降到900元,求这个单位平均每月降低的百分率是多少
某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株
(x+3)(3-0.5x)=10
解这个方程,得:x1=1, x2=2
答:要使每盆的盈利达到10元,每盆应植入4株或5株.
一个农业合作社以64000元的成本收获了某种农场品80t,目前可以以1200元/t的价格出售。如果储藏起来,每星期会损失2t,且每星期需支付各种费用1600元,但同时每星期每吨的价格将上涨200元。那么,储藏多少个星期出售这批农场品可获利122000元?
解:设储藏x个星期出售这批农场品可获利122000元,根据题意,得
(80-2x)(1200+200x)-1600x-64000=122000
整理,得 x2-30x+225=0
解得 x1=x2=15
所以,储藏15个星期出售这批农场品可获利122000元。
某公司今年10月的营业额为2500万元,按计划第四季度的总营业额要达到9100万元,求该公司11,12两个月营业额的月均增长率。
解:设该公司11,12两个月营业额的月均增长率为x,根据题意,得
2500+2500(1+x)+2500(1+x)2=9100
整理,得 x2+3x-0.64=0
解得 x1=0.2,x2=-3.2(不合题意,舍去)
所以,设该公司11,12两个月营业额的月均增长率为20%。
列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么 已知,未知之间有什么关系
2.设:设未知数,语句要完整,有单位(统一)的要注明单位;
3.列:列代数式,列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:答案也必须是完整的语句,注明单位且要贴近生活.
列方程解应用题的关键是:
寻找等量关系
作业:
习题2.10 1、2、3、4题。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
