鲁科版高中物理必修一5.1《力的合成》课件(共60张PPT)
文档属性
| 名称 | 鲁科版高中物理必修一5.1《力的合成》课件(共60张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 988.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-10-03 23:40:55 | ||
图片预览











文档简介
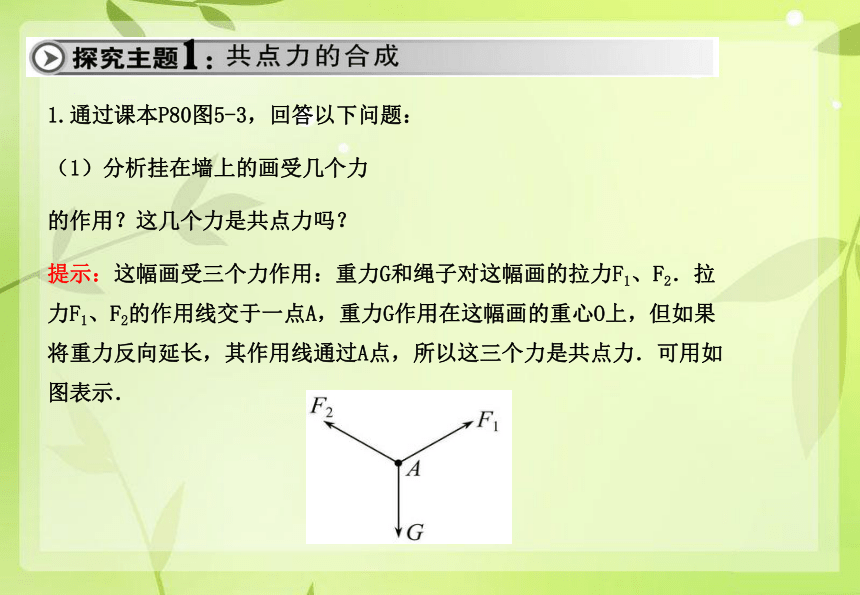
课件60张PPT。1.通过课本P80图5-3,回答以下问题:
(1)分析挂在墙上的画受几个力
的作用?这几个力是共点力吗?
提示:这幅画受三个力作用:重力G和绳子对这幅画的拉力F1、F2.拉力F1、F2的作用线交于一点A,重力G作用在这幅画的重心O上,但如果将重力反向延长,其作用线通过A点,所以这三个力是共点力.可用如图表示.(2)共点力有何特点?
提示:作用于物体的同一点或力的作用线交于一点.(3)如果用一根绳将画挂在A点,那么这一根绳的作用效果与那两根绳的作用效果相同吗?两根绳的作用力能否用这一根绳的作用力来代替?这体现了一种什么思想方法?
提示:两根细绳共同作用使画被挂起且静止,一根细绳单独作用也使画被挂起而静止,所以这一根绳的作用效果与那两根绳的作用效果完全相同.由于作用效果完全相同,所以两根绳的作用力可用这一根绳的作用力来代替.这体现了一种“等效替代”的思想方法.2.怎样计算同一直线上两个共点力F1、F2的合力?
提示:当F1、F2两个力方向相同时,合力的大小等于两个分力之和,即F合=F1+F2;当F1、F2两个力方向相反时,合力的大小等于两个分力之差,即F合=|F1-F2|,合力方向与分力中数值大的那个力方向相同.3.某位同学想把作用在两个物体上的两个力合成为一个力,他的想法是否可行?
提示:作用在不同物体上的两个力不能进行力的合成,因为它们只能对各自的物体产生力的效果,而不能产生共同的作用效果,因此不能用一个力的作用效果代替它们分别产生的效果,所以把作用在不同物体上的力合成是没有意义的,只有作用在同一物体上的力,无论力的性质如何,都可以合成,故该同学的想法不可行.可视为共点力的三种情况
(1)几个力同时作用于同一点(即力的作用点相重合)
(2)同时作用在同一个物体上的几个力,虽然作用点不重合,但是几个力的作用线正向或反向延长能够相交于同一点.
(3)当一个物体可被视为质点时,作用在物体上的几个力就可以认为是共点力.总结:
共点力的合成
1.共点力的概念:同时作用于物体的同一点,或者它们的作用线相交于同一点的几个力.
2.合力的概念:几个力共同作用所产生的效果可以用一个力来代替,这个力叫做那几个力的合力.
3.力的合成:求几个力的合力叫力的合成.典例1(2011·衡水高一检测)两个力的合力与这两个力的关系,下列说法正确的是( )
A.合力与两个力作用效果相同
B.合力与两个力在实际中是同时存在的
C.合力与两个力的作用点不同
D.对物体进行受力分析时,既要考虑这两个力,又要考虑合力解答本题需要注意以下三点:
(1)两者的作用点是否相同
(2)等效替代的含义
(3)受力分析中应画什么力思路点拨【规范解答】选A.合力与两个力是一种等效替代的关系,作用效果相同,作用点也必然相同,所以A正确C错误;合力与两个力不能同时存在,考虑合力就不再考虑这两个力,考虑这两个力就不能再考虑合力,故B、D错误. 【变式备选】将日光灯管用两悬绳吊在天花板上,设两悬绳的拉力分别为F1、F2,其合力为F,则关于灯管受力的下列说法中正确的是( )
A.灯管只受F1和F2的作用
B.灯管受F1、F2和F的共同作用
C.灯管受F1、F2、F和重力的共同作用
D.灯管受F1、F2和重力的共同作用
【解析】选D.灯管受F1、F2和重力三个力的作用,F为F1、F2的合力,可以等效替代F1、F2共同作用的效果,但受力分析时不能同时分析.1.实验探究:做课本P82实验与探究,思考探究以下问题:
(1)我们通过实验来探究力的合成的规律,如何才能方便
地研究两个分力的作用效果和一个力的作用效果是否相
同?实验中,是如何保证F1、F2与合力F的作用效果是相同
的?提示:力可以改变物体的运动状态,也可以使物体发生形变,只是用力改变物体的运动状态不如使物体发生形变容易控制,所以我们选择的是用力改变物体的形状这种方法来探究合力和两个分力的关系.实验中,两次将弹簧的结点B拉到同一个位置O处,即两次使橡皮筋的形变情况相同,我们就认为F1、F2与合力F的作用效果是相同的.(2)实验中要记录哪些数据?在记录数据时木板水平放置与竖直放置时有何区别?如何把力直观形象地表示出来?
提示:实验中要记录的数据有:O点的位置、弹簧测力计每次的示数、对应细绳的方向.木板竖直放置时,由于受测力计自身重力的影响,会使测力计的读数存在误差,所以应使木板水平放置.要想把力直观形象地表示出来需要同学们作出三个力的图示.(3)看一下两只弹簧测力计的示数之和是不是等于一只弹簧测力计的示数?力的合成是不是简单的相加减?
提示:一只弹簧测力计的读数不等于两只弹簧测力计的读数之和,而是比两只弹簧测力计读数之和小一些.可见力的合成并不是简单的相加减.(4)猜想这两个力的合力可能与这两个力的什么因素有关?
提示:因为力是矢量,两个力的合力不但与这两个力的大小有关,而且还与这两个力的方向有关.(5)在数学上,要确定三条线段的关系,常常将它们归入到一个几何图形中去进行分析比较.据此请思考合力与那两个力间存在哪些关系?
提示:表示那两个力的有向线段是平行四边形的两个邻边,表示合力的有向线段就是平行四边形中两个邻边之间的对角线.这就是合力和那两个力之间的关系——平行四边形定则. 2.演示实验:利用平行四边形演示器演示两个力F1和F2大小一定时,夹角θ在0~180°之间发生变化的情况,讨论当两个力F1与F2大小一定时,合力F与它们的夹角θ有什么关系? 合力与两个力的大小有何关系?
提示:在两个力F1、F2大小不变的情况下,两个力的夹角越大,合力越小.在两个力夹角不变的情况下,两个力越大,合力越大.合力可以大于那两个共点力,合力也可以小于那两个共点力,合力也可以等于那两个共点力.3.思考讨论:如何求多个力的合力?
提示:(1)平行四边形定则法:当三个或更多的力同时作用在一个物体上时,先用平行四边形定则求出其中两个力的合力,然后再求出这个力与第三个力的合力,依次类推,直到把所有外力都合完为止,最后得到这些力的总合力.
(2)三角形定则法:把表示所有力的矢量依次首尾相接,从第一个力的始端向最后一个力的末端画出矢量,该矢量就是所有这些力的总合力.力的平行四边形定则实验的注意事项:
(1)实验前,要先检查弹簧测力计的指针是否在零刻度线上,如果不在零刻度线上,应把指针调到零.
(2)实验中注意尽可能不使测力计的弹簧、指针、拉杆与刻度面板或限位孔发生摩擦.
(3)同一次实验中,橡皮条拉长后的结点O的位置必须保持不变.(4)画结点的位置和细线的方向也应尽量准确.用铅笔尖描出两个距离较大的点.
(5)在不超出弹簧测力计的量程和橡皮条形变的条件下,应使拉力适当大些;画力的图示时,选恰当的标度,将力的合成图作的尽量大些,以减小实验中的误差.
(6)由于实验存在误差,由作图法得到的合力F和实际测量的力F′不可能完全吻合,只要在误差允许的范围内吻合即可. 【知识归纳】共点力合成的平行四边形定则
1.定则的内容:以表示两个分力F1和F2的线段为邻边作平行四边形,那么,其合力F的大小和方向就可以用这两个邻边之间的对角线来表示.
2.适用的对象:一切矢量(如:力、位移、速度、加速度等)
3.等效定则:三角形定则4.合成规律:不在同一直线上的两个力
(1)若两个力大小不变,夹角越大时,合力越小,夹角越小时,合力越大.
(2)若两个力夹角不变时,某个力变大,合力的变化可能有以下两种情况:
①若θ≤90°,合力一定变大.
②若θ>90°,合力可能变大,也可能变小,还有可能先变小后变大.典例2 力F1=4 N,方向向东,F2=3 N,方向向北,求这两
个力的合力.
【规范解答】分别作出F1、F2的示意图,
如图所示,作出平行四边形及其
对角线.在直角三角形中:
合力F与F2的夹角为θ,则 所以
答案:5 N 北偏东53°1.互成角度的两个共点力的合成方法
(1)作图法:选定合适的标度,以F1、F2为两邻边作平行四边形,两邻边之间的对角线即为合力,根据标度用刻度尺量出合力的大小,用量角器量出合力与任意分力的夹角θ,来确定合力的方向.
(2)计算法:根据力的平行四边形定则作出力的合成示意图,然后用解三角形的知识求合力的大小和方向.
在以上两种方法中经常用到的是计算法.方法总结2.大小相等夹角θ=120°的两个分力,其合力大小等于分力大小,方向与两分力夹角α相等且α=60°.【变式备选】如图所示,夹角θ=120°的两个力作用在同一物体上,两个力的大小F1=F2=20 N,求这两个力的合力.【解析】以F1、F2为邻边作平行四边形及F1、F2所夹的对角线,如图,由于F1=F2,
故所作的平行四边形为菱形,
则合力F与F2的夹角α=60°,
所构成的两个三角形为等边
三角形,所以合力F=20 N,与F2的夹角为α=60°.典例3 六个共点力的大小分别为F、2F、3F、4F、5F、6F,相邻两力间的夹角均为60°,如图所示.试确定它们的合力的大小和方向.【思路点拨】
解答本题需要把握以下三点:
(1)明确六个共点力的特点.
(2)先将同一直线上的两个力合成.
(3)应用平行四边形定则合成大小相等,夹角为120°的两个力,最终求得合力.【规范解答】本题若将六个共点力依次逐步合成,无论是计算法还是作图法,都相当繁琐.然而,
仔细研究这六个共点力的特点,则不难
发现其中的奥秘——同一直线上的
两个力的合力均为3F,利用这一点将可大
大简化求解过程.先将六个共点力中在同
一直线上的力两两合成,结果如图所示.再根据平行四边形定则,将两侧的两个3F合成,它们的合力应与中间的3F重合.从而,最终可求得这六个力的合力为6F,与大小为5F的那个力同向.1.两个力的合力与这两个力的关系,下列说法中正确的是 ( )
A.合力比这两个力都大
B.合力至少比两个力中较小的力要大
C.合力可能比这两个力都小
D.合力可能比这两个力都大
【解析】选C、D.两个力的合力大小与两个力的大小关系为:合力可以大于两个分力、可以小于两个分力、也可以等于两个分力,故C、D正确,A、B错误.复习巩固2.(2011·石家庄高一检测)在做“验证力的平行四边形定则”实验中采用的科学方法是( )
A.理想实验法 B.等效替代法
C.控制变量法 D.建立物理模型法【解析】选B.本实验中,两个弹簧测力计的拉力可以把橡皮条的结点拉到O位置,只用一个弹簧测力计同样能把橡皮条的结点拉到同一位置O,两个弹簧测力计的拉力效果与一个弹簧测力计的拉力效果相同,两个弹簧测力计的拉力与一个弹簧测力计的拉力可以相互替代.因此本实验中采用的科学方法为等效替代法.3.(2011·郑州高一检测)两个共点力F1与F2的合力大小为6 N,则F1与F2的大小可能是( )
A.F1=2 N,F2=9 N B.F1=4 N,F2=8 N
C.F1=1 N,F2=8 N D.F1=2 N,F2=1 N
【解析】选B. 两个共点力F1与F2的合力大小范围为
|F1-F2|≤F≤F1+F2,A选项中7 N≤F≤11 N,B选项中
4 N≤F≤12 N,C选项中7 N≤F≤9 N,D选项中
1 N≤F≤3 N,6 N在其范围之内的只有B选项,故B正确.4.抬花轿是我国传统文化习俗之一,
同样一个花轿可以双人抬,也可以
四人抬,二者比较,下列说法
正确的是( )
A.双人抬时支持力的合力比四人抬时支持力的合力大
B.双人抬时支持力的合力比四人抬时支持力的合力小
C.双人抬时支持力的合力与四人抬时支持力的合力一样大
D.双人抬时其中一个人的支持力与四人抬时其中一个人的支持力一样大【解析】选C.双人抬时支持力的合力与四人抬时支持力的合力都等于花轿的重力,所以一样大,A、B错,C对.双人抬时其中一个人的支持力大于四个人抬时其中一个人的支持力,D错.5.有两个力,它们的合力为零.现把其中一个向东的6 N的
力改为向南(大小不变),它们的合力大小、方向如何?
【解析】两个力合力为零,则这两个力一定是等大反向
的,大小都为6 N,其中一个力向东,则另一个力一定
向西.当把其中一个向东的6 N的力改为向南后,
两力的关系如图所示,在直角三角形中,
根据勾股定理可得合力
θ=45°,即方向西偏南45°.一、选择题(本大题共6小题,每小题5分,共30分)
1.关于两个大小不变的共点力与其合力的关系,下列说法正确的是( )
A.合力的大小随两力夹角的增大而增大
B.当两个力的方向相同时,合力最小
C.两个力的夹角小于180°时,合力的大小随夹角的减小而增大
D.合力的大小不能小于两力中最小者能力提升【解析】选C.两个大小不变的共点力,当两个力的夹角小于180°时,合力的大小随夹角的减小而增大,随夹角的增大而减小,A错误,C正确;当两个力的方向相同时,合力最大,B错误;合力大小可以大于两个力,可以小于两个力,也可以等于两个力,D错误.2.如图所示,F1、F2为两个分力,F为合力,则正确的合力矢量图为( )
【解析】选A、C.由平行四边形定则的内容可知,A正确,B错误;由三角形定则的内容可知,C正确;D选项中反映的是F1与F的合力等于F2,D错误.3.两个共点力F1、F2的大小不变,它们的合力F跟两力F1、F2之间的夹角θ的关系如图所示,则两个力的大小可能为( )
A.3 N 4 N B.3 N 5 N
C.2 N 6 N D.1 N 7 N 【解析】选A.由图象可知,当θ=90°时,两个力F1、F2
垂直,此时合力F=5 N,则有 即
当θ=180°时,两个力F1、F2反向,此时合力F=1 N,即
|F1-F2|=1 N.由以上两式解得F1=4 N,F2=3 N或F1=3 N,
F2=4 N,故正确答案为A.4.(2011·深圳高一检测)有三个力,大小分别为13 N、
3 N、29 N.那么这三个力的合力最大值和最小值应该是( )
A.29 N,3 N B.45 N, 0 N
C.45 N,13 N D.29 N,13 N
【解析】选C.当三个力同方向时,合力最大,为45 N;任取其中两个力,如取13 N、3 N两个力,其合力范围为
10 N≤F≤16 N,29 N不在该范围之内,故合力不能为零,当13 N、3 N的两个力同向,与29 N的力反向时,合力最小,最小值为13 N,故C正确.5.(2011·马鞍山高一检测)图中三角形的三边各代表一个力,以下说法中正确的是( )
A.图①中三个力的合力为零
B.图②中三个力的合力为2F3
C.图③中三个力的合力为2F1
D.图④中三个力的合力为2F2【解析】选C.在图①中F1、F2的合力为F3,所以三个力的合力为2F3,A错误;图②中F1 、F3的合力为F2,所以三个力的合力为2F2,B错误;图③中F3 、F2的合力为F1,所以三个力的合力为2F1,C正确;图④中F1、F2的合力为-F3,所以三个力的合力为零,D错误.6.(2011·南岸区高一检测)在图中,
AO、BO、CO是三条完全相同的轻绳,
并将铁棒水平吊起,若铁棒足够重时,
绳AO先断,则( )
A.θ=120°
B.θ>120°
C.θ<120°
D.不论θ为何值,AO总是先断【解析】选C.由于绳AO先断,说明绳AO上的弹力大于绳BO、CO上的弹力,根据平行四边形定则和三角形知识可得BO和CO两绳上拉力的合力大小恰好等于AO上的拉力,则:当角为120°时,AO、BO、CO三绳上的拉力相等.当角大于120°时AO绳上的拉力将小于BO、CO绳上的拉力.当角小于120°时,AO绳上的拉力将大于BO、CO绳上的拉力,故C正确.二、非选择题(本大题共2小题,共20分,要有必要的文字叙述和解题步骤)
7.(10分)(2010·天津高考)在探究合力的方法时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳.实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧测力计互成角度地拉橡皮条,另一次是用一个弹簧测力计通过细绳拉橡皮条.(1)实验对两次拉伸橡皮条的要求中,下列哪些说法是正确的___________(填字母代号)
A.将橡皮条拉伸相同长度即可
B.将橡皮条沿相同方向拉到相同长度
C.将弹簧测力计都拉伸到相同刻度即可
D.将橡皮条和绳的结点拉到相同位置(2)同学们在操作过程中有如下议论,其中对减小实验误差有益的说法是____________(填字母代号)
A.两细绳必须等长
B.弹簧测力计、细绳、橡皮条都应与木板平行
C.用两弹簧测力计同时拉细绳时两弹簧测力计示数之差应尽可能大
D.拉橡皮条的细绳要长些,标记同一细绳方向的两点要远些【解析】(1)实验中两次拉伸橡皮条时,应要求两次的作用效果必须完全相同,即橡皮条被拉伸的方向、长度完全相同,所以答案选B、D.
(2)对减小误差有益的做法是B、D.B做法能保证分力与合力在同一平面内,减小了作图误差;D做法能保证分力的方向测量更准确,减小了测量误差.实验时两细绳不必等长,两弹簧测力计的示数也不一定要求相差较大,所以B、D正确.
答案:(1)B、D (2)B、D8.(10分)如图所示,一名
骑独轮车的杂技演员在空中
钢索上表演,如果演员和
独轮车的总质量为80 kg,两侧的钢索互成150°夹角,求钢索所受拉力有多大?(cos 75°=0.259,g取10 N/kg)【解析】设钢索的拉力大小为F,则演员两侧的钢索的合力
与演员和独轮车的总重力等大反向.作出拉力与其合力的平
行四边形为一菱形,如图所示,据几何知识可知
所以拉力:
答案:1 544 N 【规律方法】求解三种特殊情况下两个共点力合力的方法在力的合成中,用得最多的是计算法,即当两力夹角θ等于任意角度时,F1、F2的合力可由平行四边形定则作出,然后根据三角形的知识可求得合力.而在计算法中,经常会遇到以下三种特殊情况,对于这三种特殊情况,其求解方法如下:(1)当两个力F1、F2互相垂直时,如图甲,合力
合力与其中分力F1的夹角为 由三角形知识知:
由此可确定合力的方向.
(2)两个夹角为θ、
大小相等的力的合成,
如图乙所示,作出的
平行四边形为菱形,利用其对角线互相垂直的特点,可得
直角三角形,解直角三角形求得合力
合力与每一个分力的夹角都等于(3)夹角为120°的两个等大的
力的合成,如图丙所示,实际上
是(2)中的特殊情况:
即合力的大小等于分力,合力与每一个分力的夹角均
为60°.
(1)分析挂在墙上的画受几个力
的作用?这几个力是共点力吗?
提示:这幅画受三个力作用:重力G和绳子对这幅画的拉力F1、F2.拉力F1、F2的作用线交于一点A,重力G作用在这幅画的重心O上,但如果将重力反向延长,其作用线通过A点,所以这三个力是共点力.可用如图表示.(2)共点力有何特点?
提示:作用于物体的同一点或力的作用线交于一点.(3)如果用一根绳将画挂在A点,那么这一根绳的作用效果与那两根绳的作用效果相同吗?两根绳的作用力能否用这一根绳的作用力来代替?这体现了一种什么思想方法?
提示:两根细绳共同作用使画被挂起且静止,一根细绳单独作用也使画被挂起而静止,所以这一根绳的作用效果与那两根绳的作用效果完全相同.由于作用效果完全相同,所以两根绳的作用力可用这一根绳的作用力来代替.这体现了一种“等效替代”的思想方法.2.怎样计算同一直线上两个共点力F1、F2的合力?
提示:当F1、F2两个力方向相同时,合力的大小等于两个分力之和,即F合=F1+F2;当F1、F2两个力方向相反时,合力的大小等于两个分力之差,即F合=|F1-F2|,合力方向与分力中数值大的那个力方向相同.3.某位同学想把作用在两个物体上的两个力合成为一个力,他的想法是否可行?
提示:作用在不同物体上的两个力不能进行力的合成,因为它们只能对各自的物体产生力的效果,而不能产生共同的作用效果,因此不能用一个力的作用效果代替它们分别产生的效果,所以把作用在不同物体上的力合成是没有意义的,只有作用在同一物体上的力,无论力的性质如何,都可以合成,故该同学的想法不可行.可视为共点力的三种情况
(1)几个力同时作用于同一点(即力的作用点相重合)
(2)同时作用在同一个物体上的几个力,虽然作用点不重合,但是几个力的作用线正向或反向延长能够相交于同一点.
(3)当一个物体可被视为质点时,作用在物体上的几个力就可以认为是共点力.总结:
共点力的合成
1.共点力的概念:同时作用于物体的同一点,或者它们的作用线相交于同一点的几个力.
2.合力的概念:几个力共同作用所产生的效果可以用一个力来代替,这个力叫做那几个力的合力.
3.力的合成:求几个力的合力叫力的合成.典例1(2011·衡水高一检测)两个力的合力与这两个力的关系,下列说法正确的是( )
A.合力与两个力作用效果相同
B.合力与两个力在实际中是同时存在的
C.合力与两个力的作用点不同
D.对物体进行受力分析时,既要考虑这两个力,又要考虑合力解答本题需要注意以下三点:
(1)两者的作用点是否相同
(2)等效替代的含义
(3)受力分析中应画什么力思路点拨【规范解答】选A.合力与两个力是一种等效替代的关系,作用效果相同,作用点也必然相同,所以A正确C错误;合力与两个力不能同时存在,考虑合力就不再考虑这两个力,考虑这两个力就不能再考虑合力,故B、D错误. 【变式备选】将日光灯管用两悬绳吊在天花板上,设两悬绳的拉力分别为F1、F2,其合力为F,则关于灯管受力的下列说法中正确的是( )
A.灯管只受F1和F2的作用
B.灯管受F1、F2和F的共同作用
C.灯管受F1、F2、F和重力的共同作用
D.灯管受F1、F2和重力的共同作用
【解析】选D.灯管受F1、F2和重力三个力的作用,F为F1、F2的合力,可以等效替代F1、F2共同作用的效果,但受力分析时不能同时分析.1.实验探究:做课本P82实验与探究,思考探究以下问题:
(1)我们通过实验来探究力的合成的规律,如何才能方便
地研究两个分力的作用效果和一个力的作用效果是否相
同?实验中,是如何保证F1、F2与合力F的作用效果是相同
的?提示:力可以改变物体的运动状态,也可以使物体发生形变,只是用力改变物体的运动状态不如使物体发生形变容易控制,所以我们选择的是用力改变物体的形状这种方法来探究合力和两个分力的关系.实验中,两次将弹簧的结点B拉到同一个位置O处,即两次使橡皮筋的形变情况相同,我们就认为F1、F2与合力F的作用效果是相同的.(2)实验中要记录哪些数据?在记录数据时木板水平放置与竖直放置时有何区别?如何把力直观形象地表示出来?
提示:实验中要记录的数据有:O点的位置、弹簧测力计每次的示数、对应细绳的方向.木板竖直放置时,由于受测力计自身重力的影响,会使测力计的读数存在误差,所以应使木板水平放置.要想把力直观形象地表示出来需要同学们作出三个力的图示.(3)看一下两只弹簧测力计的示数之和是不是等于一只弹簧测力计的示数?力的合成是不是简单的相加减?
提示:一只弹簧测力计的读数不等于两只弹簧测力计的读数之和,而是比两只弹簧测力计读数之和小一些.可见力的合成并不是简单的相加减.(4)猜想这两个力的合力可能与这两个力的什么因素有关?
提示:因为力是矢量,两个力的合力不但与这两个力的大小有关,而且还与这两个力的方向有关.(5)在数学上,要确定三条线段的关系,常常将它们归入到一个几何图形中去进行分析比较.据此请思考合力与那两个力间存在哪些关系?
提示:表示那两个力的有向线段是平行四边形的两个邻边,表示合力的有向线段就是平行四边形中两个邻边之间的对角线.这就是合力和那两个力之间的关系——平行四边形定则. 2.演示实验:利用平行四边形演示器演示两个力F1和F2大小一定时,夹角θ在0~180°之间发生变化的情况,讨论当两个力F1与F2大小一定时,合力F与它们的夹角θ有什么关系? 合力与两个力的大小有何关系?
提示:在两个力F1、F2大小不变的情况下,两个力的夹角越大,合力越小.在两个力夹角不变的情况下,两个力越大,合力越大.合力可以大于那两个共点力,合力也可以小于那两个共点力,合力也可以等于那两个共点力.3.思考讨论:如何求多个力的合力?
提示:(1)平行四边形定则法:当三个或更多的力同时作用在一个物体上时,先用平行四边形定则求出其中两个力的合力,然后再求出这个力与第三个力的合力,依次类推,直到把所有外力都合完为止,最后得到这些力的总合力.
(2)三角形定则法:把表示所有力的矢量依次首尾相接,从第一个力的始端向最后一个力的末端画出矢量,该矢量就是所有这些力的总合力.力的平行四边形定则实验的注意事项:
(1)实验前,要先检查弹簧测力计的指针是否在零刻度线上,如果不在零刻度线上,应把指针调到零.
(2)实验中注意尽可能不使测力计的弹簧、指针、拉杆与刻度面板或限位孔发生摩擦.
(3)同一次实验中,橡皮条拉长后的结点O的位置必须保持不变.(4)画结点的位置和细线的方向也应尽量准确.用铅笔尖描出两个距离较大的点.
(5)在不超出弹簧测力计的量程和橡皮条形变的条件下,应使拉力适当大些;画力的图示时,选恰当的标度,将力的合成图作的尽量大些,以减小实验中的误差.
(6)由于实验存在误差,由作图法得到的合力F和实际测量的力F′不可能完全吻合,只要在误差允许的范围内吻合即可. 【知识归纳】共点力合成的平行四边形定则
1.定则的内容:以表示两个分力F1和F2的线段为邻边作平行四边形,那么,其合力F的大小和方向就可以用这两个邻边之间的对角线来表示.
2.适用的对象:一切矢量(如:力、位移、速度、加速度等)
3.等效定则:三角形定则4.合成规律:不在同一直线上的两个力
(1)若两个力大小不变,夹角越大时,合力越小,夹角越小时,合力越大.
(2)若两个力夹角不变时,某个力变大,合力的变化可能有以下两种情况:
①若θ≤90°,合力一定变大.
②若θ>90°,合力可能变大,也可能变小,还有可能先变小后变大.典例2 力F1=4 N,方向向东,F2=3 N,方向向北,求这两
个力的合力.
【规范解答】分别作出F1、F2的示意图,
如图所示,作出平行四边形及其
对角线.在直角三角形中:
合力F与F2的夹角为θ,则 所以
答案:5 N 北偏东53°1.互成角度的两个共点力的合成方法
(1)作图法:选定合适的标度,以F1、F2为两邻边作平行四边形,两邻边之间的对角线即为合力,根据标度用刻度尺量出合力的大小,用量角器量出合力与任意分力的夹角θ,来确定合力的方向.
(2)计算法:根据力的平行四边形定则作出力的合成示意图,然后用解三角形的知识求合力的大小和方向.
在以上两种方法中经常用到的是计算法.方法总结2.大小相等夹角θ=120°的两个分力,其合力大小等于分力大小,方向与两分力夹角α相等且α=60°.【变式备选】如图所示,夹角θ=120°的两个力作用在同一物体上,两个力的大小F1=F2=20 N,求这两个力的合力.【解析】以F1、F2为邻边作平行四边形及F1、F2所夹的对角线,如图,由于F1=F2,
故所作的平行四边形为菱形,
则合力F与F2的夹角α=60°,
所构成的两个三角形为等边
三角形,所以合力F=20 N,与F2的夹角为α=60°.典例3 六个共点力的大小分别为F、2F、3F、4F、5F、6F,相邻两力间的夹角均为60°,如图所示.试确定它们的合力的大小和方向.【思路点拨】
解答本题需要把握以下三点:
(1)明确六个共点力的特点.
(2)先将同一直线上的两个力合成.
(3)应用平行四边形定则合成大小相等,夹角为120°的两个力,最终求得合力.【规范解答】本题若将六个共点力依次逐步合成,无论是计算法还是作图法,都相当繁琐.然而,
仔细研究这六个共点力的特点,则不难
发现其中的奥秘——同一直线上的
两个力的合力均为3F,利用这一点将可大
大简化求解过程.先将六个共点力中在同
一直线上的力两两合成,结果如图所示.再根据平行四边形定则,将两侧的两个3F合成,它们的合力应与中间的3F重合.从而,最终可求得这六个力的合力为6F,与大小为5F的那个力同向.1.两个力的合力与这两个力的关系,下列说法中正确的是 ( )
A.合力比这两个力都大
B.合力至少比两个力中较小的力要大
C.合力可能比这两个力都小
D.合力可能比这两个力都大
【解析】选C、D.两个力的合力大小与两个力的大小关系为:合力可以大于两个分力、可以小于两个分力、也可以等于两个分力,故C、D正确,A、B错误.复习巩固2.(2011·石家庄高一检测)在做“验证力的平行四边形定则”实验中采用的科学方法是( )
A.理想实验法 B.等效替代法
C.控制变量法 D.建立物理模型法【解析】选B.本实验中,两个弹簧测力计的拉力可以把橡皮条的结点拉到O位置,只用一个弹簧测力计同样能把橡皮条的结点拉到同一位置O,两个弹簧测力计的拉力效果与一个弹簧测力计的拉力效果相同,两个弹簧测力计的拉力与一个弹簧测力计的拉力可以相互替代.因此本实验中采用的科学方法为等效替代法.3.(2011·郑州高一检测)两个共点力F1与F2的合力大小为6 N,则F1与F2的大小可能是( )
A.F1=2 N,F2=9 N B.F1=4 N,F2=8 N
C.F1=1 N,F2=8 N D.F1=2 N,F2=1 N
【解析】选B. 两个共点力F1与F2的合力大小范围为
|F1-F2|≤F≤F1+F2,A选项中7 N≤F≤11 N,B选项中
4 N≤F≤12 N,C选项中7 N≤F≤9 N,D选项中
1 N≤F≤3 N,6 N在其范围之内的只有B选项,故B正确.4.抬花轿是我国传统文化习俗之一,
同样一个花轿可以双人抬,也可以
四人抬,二者比较,下列说法
正确的是( )
A.双人抬时支持力的合力比四人抬时支持力的合力大
B.双人抬时支持力的合力比四人抬时支持力的合力小
C.双人抬时支持力的合力与四人抬时支持力的合力一样大
D.双人抬时其中一个人的支持力与四人抬时其中一个人的支持力一样大【解析】选C.双人抬时支持力的合力与四人抬时支持力的合力都等于花轿的重力,所以一样大,A、B错,C对.双人抬时其中一个人的支持力大于四个人抬时其中一个人的支持力,D错.5.有两个力,它们的合力为零.现把其中一个向东的6 N的
力改为向南(大小不变),它们的合力大小、方向如何?
【解析】两个力合力为零,则这两个力一定是等大反向
的,大小都为6 N,其中一个力向东,则另一个力一定
向西.当把其中一个向东的6 N的力改为向南后,
两力的关系如图所示,在直角三角形中,
根据勾股定理可得合力
θ=45°,即方向西偏南45°.一、选择题(本大题共6小题,每小题5分,共30分)
1.关于两个大小不变的共点力与其合力的关系,下列说法正确的是( )
A.合力的大小随两力夹角的增大而增大
B.当两个力的方向相同时,合力最小
C.两个力的夹角小于180°时,合力的大小随夹角的减小而增大
D.合力的大小不能小于两力中最小者能力提升【解析】选C.两个大小不变的共点力,当两个力的夹角小于180°时,合力的大小随夹角的减小而增大,随夹角的增大而减小,A错误,C正确;当两个力的方向相同时,合力最大,B错误;合力大小可以大于两个力,可以小于两个力,也可以等于两个力,D错误.2.如图所示,F1、F2为两个分力,F为合力,则正确的合力矢量图为( )
【解析】选A、C.由平行四边形定则的内容可知,A正确,B错误;由三角形定则的内容可知,C正确;D选项中反映的是F1与F的合力等于F2,D错误.3.两个共点力F1、F2的大小不变,它们的合力F跟两力F1、F2之间的夹角θ的关系如图所示,则两个力的大小可能为( )
A.3 N 4 N B.3 N 5 N
C.2 N 6 N D.1 N 7 N 【解析】选A.由图象可知,当θ=90°时,两个力F1、F2
垂直,此时合力F=5 N,则有 即
当θ=180°时,两个力F1、F2反向,此时合力F=1 N,即
|F1-F2|=1 N.由以上两式解得F1=4 N,F2=3 N或F1=3 N,
F2=4 N,故正确答案为A.4.(2011·深圳高一检测)有三个力,大小分别为13 N、
3 N、29 N.那么这三个力的合力最大值和最小值应该是( )
A.29 N,3 N B.45 N, 0 N
C.45 N,13 N D.29 N,13 N
【解析】选C.当三个力同方向时,合力最大,为45 N;任取其中两个力,如取13 N、3 N两个力,其合力范围为
10 N≤F≤16 N,29 N不在该范围之内,故合力不能为零,当13 N、3 N的两个力同向,与29 N的力反向时,合力最小,最小值为13 N,故C正确.5.(2011·马鞍山高一检测)图中三角形的三边各代表一个力,以下说法中正确的是( )
A.图①中三个力的合力为零
B.图②中三个力的合力为2F3
C.图③中三个力的合力为2F1
D.图④中三个力的合力为2F2【解析】选C.在图①中F1、F2的合力为F3,所以三个力的合力为2F3,A错误;图②中F1 、F3的合力为F2,所以三个力的合力为2F2,B错误;图③中F3 、F2的合力为F1,所以三个力的合力为2F1,C正确;图④中F1、F2的合力为-F3,所以三个力的合力为零,D错误.6.(2011·南岸区高一检测)在图中,
AO、BO、CO是三条完全相同的轻绳,
并将铁棒水平吊起,若铁棒足够重时,
绳AO先断,则( )
A.θ=120°
B.θ>120°
C.θ<120°
D.不论θ为何值,AO总是先断【解析】选C.由于绳AO先断,说明绳AO上的弹力大于绳BO、CO上的弹力,根据平行四边形定则和三角形知识可得BO和CO两绳上拉力的合力大小恰好等于AO上的拉力,则:当角为120°时,AO、BO、CO三绳上的拉力相等.当角大于120°时AO绳上的拉力将小于BO、CO绳上的拉力.当角小于120°时,AO绳上的拉力将大于BO、CO绳上的拉力,故C正确.二、非选择题(本大题共2小题,共20分,要有必要的文字叙述和解题步骤)
7.(10分)(2010·天津高考)在探究合力的方法时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳.实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧测力计互成角度地拉橡皮条,另一次是用一个弹簧测力计通过细绳拉橡皮条.(1)实验对两次拉伸橡皮条的要求中,下列哪些说法是正确的___________(填字母代号)
A.将橡皮条拉伸相同长度即可
B.将橡皮条沿相同方向拉到相同长度
C.将弹簧测力计都拉伸到相同刻度即可
D.将橡皮条和绳的结点拉到相同位置(2)同学们在操作过程中有如下议论,其中对减小实验误差有益的说法是____________(填字母代号)
A.两细绳必须等长
B.弹簧测力计、细绳、橡皮条都应与木板平行
C.用两弹簧测力计同时拉细绳时两弹簧测力计示数之差应尽可能大
D.拉橡皮条的细绳要长些,标记同一细绳方向的两点要远些【解析】(1)实验中两次拉伸橡皮条时,应要求两次的作用效果必须完全相同,即橡皮条被拉伸的方向、长度完全相同,所以答案选B、D.
(2)对减小误差有益的做法是B、D.B做法能保证分力与合力在同一平面内,减小了作图误差;D做法能保证分力的方向测量更准确,减小了测量误差.实验时两细绳不必等长,两弹簧测力计的示数也不一定要求相差较大,所以B、D正确.
答案:(1)B、D (2)B、D8.(10分)如图所示,一名
骑独轮车的杂技演员在空中
钢索上表演,如果演员和
独轮车的总质量为80 kg,两侧的钢索互成150°夹角,求钢索所受拉力有多大?(cos 75°=0.259,g取10 N/kg)【解析】设钢索的拉力大小为F,则演员两侧的钢索的合力
与演员和独轮车的总重力等大反向.作出拉力与其合力的平
行四边形为一菱形,如图所示,据几何知识可知
所以拉力:
答案:1 544 N 【规律方法】求解三种特殊情况下两个共点力合力的方法在力的合成中,用得最多的是计算法,即当两力夹角θ等于任意角度时,F1、F2的合力可由平行四边形定则作出,然后根据三角形的知识可求得合力.而在计算法中,经常会遇到以下三种特殊情况,对于这三种特殊情况,其求解方法如下:(1)当两个力F1、F2互相垂直时,如图甲,合力
合力与其中分力F1的夹角为 由三角形知识知:
由此可确定合力的方向.
(2)两个夹角为θ、
大小相等的力的合成,
如图乙所示,作出的
平行四边形为菱形,利用其对角线互相垂直的特点,可得
直角三角形,解直角三角形求得合力
合力与每一个分力的夹角都等于(3)夹角为120°的两个等大的
力的合成,如图丙所示,实际上
是(2)中的特殊情况:
即合力的大小等于分力,合力与每一个分力的夹角均
为60°.
同课章节目录
- 第1章 绪论
- 物理学与自然规律
- 物理学与社会发展
- 怎样学习物理学
- 高中物理教材特点
- 第2章 运动的描述
- 导入 认识运动
- 第1节 运动、空间和时间
- 第2节 质点和位移
- 第3节 速度和加速度
- 第3章 匀变速直线运动的研究
- 导入 速度的变化
- 第1节 匀变速直线运动的规律
- 第2节 匀变速直线运动的实验探究
- 第3节 匀变速直线运动实例-自由落体运动
- 第4章 相互作用
- 导入 奇特的力现象
- 第1节 重力与重心
- 第2节 形变与弹力
- 第3节 摩擦力
- 第5章 力与平衡
- 导入 感悟平衡之美
- 第1节 力的合成
- 第2节 力的分解
- 第3节 力的平衡
- 第4节 平衡条件的应用
- 第6章 力与运动
- 导入 跨越时空的对话
- 第1节 牛顿第一定律
- 第2节 牛顿第二定律
- 第3节 牛顿第三定律
- 第4节 超重与失重
- 本章复习与测试
